How to Subtract Numbers with Formula and Solved Examples
Subtraction is an operation in which we take something out of a collection of objects. For example, taking out 4 mangoes from 7 mangoes. It is an arithmetic operation between two numbers. It has great significance in mathematics since it forms the base for our mathematical understanding. Let us learn how to subtract the numbers.
What is Subtraction?
It is an arithmetic operation that signifies the removal of several objects from a collection. In other words, suppose you have 5 Apples, and you ate 3 of them, then you are left with only 2 Apples, this course of an arithmetic operation is called subtraction. This is the most basic form of math we use daily. From shopping to handling a business.
Subtraction
Why is Subtraction Important?
Subtraction is the backbone of the number system. We use it on an everyday basis. Suppose you go to the supermarket to buy vegetables, and the potatoes cost 20 rupees per kilogram, you buy a total of 4 kilograms of potatoes, and you have a total of 110 rupees, then how much are you left with? The answer is simple, you have to pay \[20 \times 4 = 80\] rupees, and you have 110 rupees. After paying 80 rupees to the shopkeeper your balance amount is \[110 - 80 = 30\] rupees. Don’t fret. We will learn how to subtract two numbers in just a moment.
How to Subtract Two Numbers?
We will learn how to subtract two numbers. These are the steps to subtracting two numbers.
Write down the larger the number. Let's take an example where we want to subtract 17 from 32.
Write the smaller number right below, the larger number. Do not forget to line up the ones, tens, and hundreds,... Places. In our case 7 is directly below 2 and 1 is directly below 3.
Subtraction
Start subtracting the numbers from right to left. If the digit above is greater than the lower one, we do simple subtraction, and if the number above is lesser than the lower one, we borrow 1 from the digit next to the upper one on the left, cross off the digit and make it 1 less than it was. For example, in our case, we have to subtract 7 from 2, so we borrow 1 from 3, and it makes 12, so instead of subtracting 7 from 2, now we have to subtract 7 from 12, and we also cross off 3 and write 2 in place of it. So \[12 - 7 = 5\].
Subtraction
Now we subtract the tens place digit, which is \[2 - 1 = 1\]
Subtraction
Therefore our final answer is 15. Check the answer, \[17 + 15 = 32\].
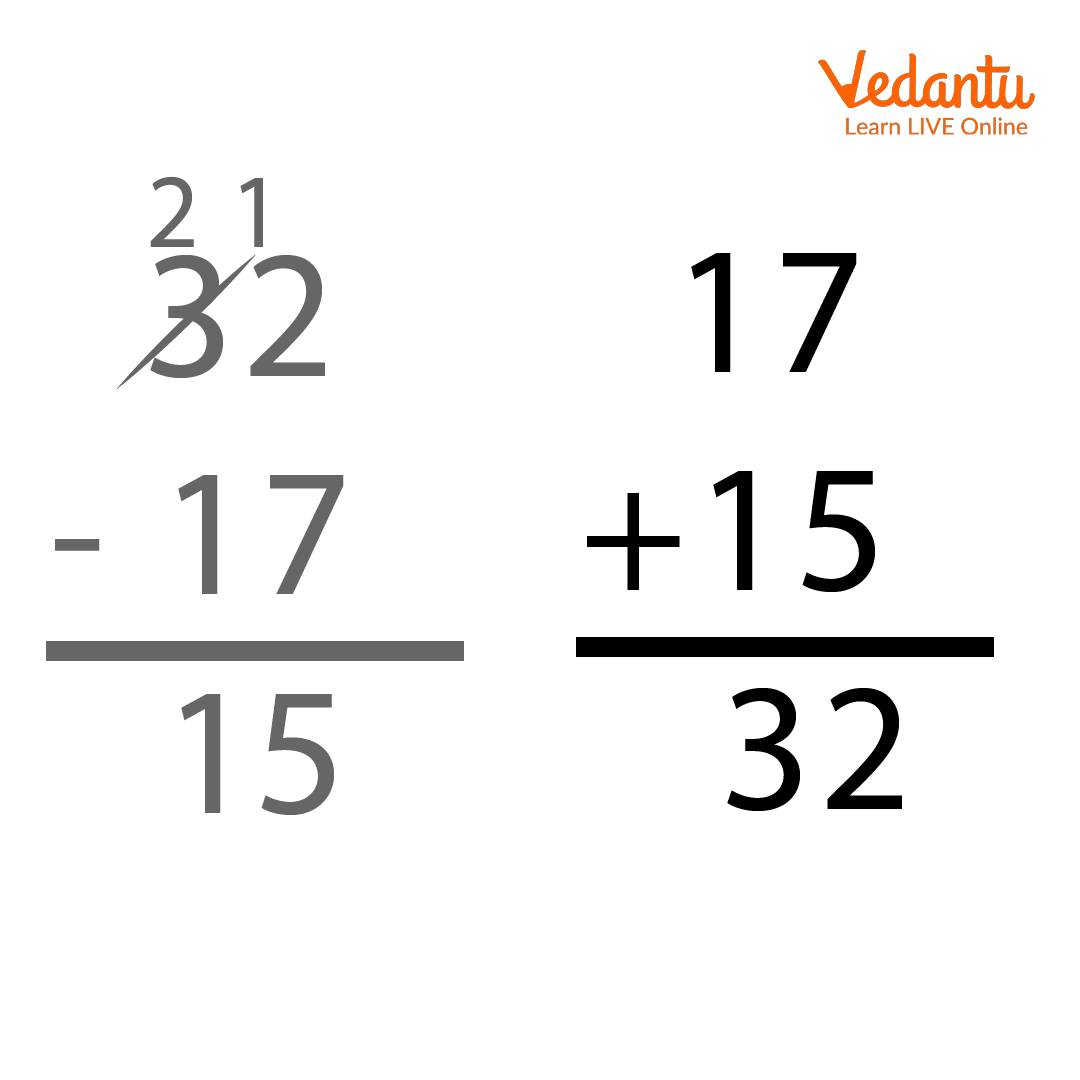
Subtraction
Important Notes
Here are some of the important notes.
If a smaller number is subtracted from a big number, then the answer is always a positive number.
If a bigger number is subtracted from a small number, then the answer is always a negative number.
If a number is subtracted from itself, we get 0 as the answer. For example, 7 subtracted from 7 is 0, and 863 subtracted from 863 is 0.
Great! You now understand what subtraction of numbers is. You have learned how to subtract two numbers and how to do it step by step. Apart from this, you have also learned some important facts about subtraction. Now subtract the following numbers given in the worksheet below:
Solved Examples
1. Sophie has 27 pens, she sold 15 pens out of those 27 pens. How many pens are left at Sophie?
Ans: Sophia has 27 pens, and she sold 15 pens; we can see that the problem asks for the subtraction of two numbers. Here we have to subtract 15 out of 27 to find the number of chocolates left to Sophia. So we have \[27 - 15\]. \[7 - 5\] is 2 and \[2 - 1\] is 1. Hence \[27 - 15\] is 12.
Subtraction
2. It's your birthday, and you have brought 100 chocolates. You have 5 friends; you decided to give them 10, 10,10,20, and 20 chocolates. How many chocolates are you left with?
Ans: This problem asks for two things, first, we have to calculate how many total chocolates has he given to his friends then we will have to find the number of chocolates left by him. So the total number of chocolates he has given is\[10 + 10 + 10 + 20 + 20 = 70\]. Now we have to subtract this number from the total number of chocolates to see how many chocolates are still left. So we have to subtract 70 from 100. 0 - 0 is 0 and then we have \[0 - 7\] in the tens place. 0 is less than 7, so we borrow 1 from 1 and then subtract 7. So \[10 - 7 = 3\] hence \[100 - 70 = 30\]. Thus, only 30 chocolates are left for you.
Subtraction
Conclusion
Subtraction is very vital in our daily life. And it is the very base of mathematical reasoning. We use it in many fields of mathematics, as well as in our daily lives. It is a fundamental arithmetic operation, yet the most important is just like addition, multiplication, and division.
FAQs on Subtraction of Numbers Explained for Students
1. What is subtraction in mathematics?
Subtraction is the mathematical operation of finding the difference between two numbers. It tells us how much one number is less than another. In subtraction, the number being subtracted is called the subtrahend, the number from which it is subtracted is the minuend, and the result is the difference. For example: 9 − 4 = 5.
2. What is the formula for subtraction?
The basic formula for subtraction is Minuend − Subtrahend = Difference. In symbols: a − b = c, where:
- a is the minuend
- b is the subtrahend
- c is the difference
3. How do you subtract numbers step by step?
To subtract numbers, align place values and subtract digit by digit from right to left. Follow these steps:
- Step 1: Write numbers in columns (ones, tens, hundreds).
- Step 2: Start subtracting from the ones place.
- Step 3: Borrow from the next place if the top digit is smaller.
- Step 4: Continue moving left.
4. How do you subtract with borrowing?
Subtraction with borrowing is used when the top digit is smaller than the bottom digit in a column. You borrow 1 from the next higher place value and add 10 to the current digit. Example: 43 − 27:
- Borrow 1 from 4 → becomes 3.
- 13 − 7 = 6
- 3 − 2 = 1
5. What is the difference between addition and subtraction?
Addition combines numbers to find the sum, while subtraction finds the difference between numbers. Key differences:
- Addition increases value (e.g., 5 + 3 = 8).
- Subtraction decreases value (e.g., 5 − 3 = 2).
- Addition uses the + symbol; subtraction uses the − symbol.
6. Can subtraction result in a negative number?
Yes, subtraction results in a negative number when the subtrahend is greater than the minuend. Example: 4 − 9 = −5. This means the result is below zero on the number line, which introduces the concept of negative numbers.
7. How do you subtract decimals?
To subtract decimals, line up the decimal points and subtract as with whole numbers. Steps:
- Align decimal points vertically.
- Add zeros if needed.
- Subtract from right to left.
8. How do you subtract fractions?
To subtract fractions, make the denominators the same and subtract the numerators. Formula: a/b − c/b = (a − c)/b. Example: 7/8 − 3/8 = 4/8 = 1/2. If denominators are different, first find a common denominator.
9. What are the properties of subtraction?
Subtraction does not follow the commutative or associative properties. Important properties include:
- Not commutative: a − b ≠ b − a
- Not associative: (a − b) − c ≠ a − (b − c)
- Identity property: a − 0 = a
10. What are common mistakes in subtraction?
Common subtraction mistakes include incorrect borrowing and misaligning place values. Watch out for:
- Forgetting to borrow correctly
- Not lining up digits by place value
- Ignoring negative signs
- Subtracting in the wrong order
