




What is Unit Square?
Have you ever eaten dairy milk chocolate? Then surely you would have seen the shape of each piece? Can you tell what is the shape of each piece? Though the shape of the chocolate is rectangular, however each of its pieces is square in shape. A square is a shape with all its sides equal in length. Can we count the number of its sides? Yes, you can, it is 4.
Now, a question arises, what is a unit square? Let us understand the unit square definition along with solutions to certain questions that might arise in your mind while looking into this topic.
Unit Square Definition
Like any other square, a unit square is a two-dimensional shape having four sides. And, the major point to be focussed on is that the length of all four sides is equal to 1 unit. A unit square is also called a ‘Square of Side 1’. It has four sides which are unit squares.

Unit Square
Area of a Unit Square
We know that the area of a square is calculated as:
Area = side x side = (side)2
To evaluate the area of a unit square, we know that the side of a square is 1 unit. Therefore,
Area of unit square = 1 x 1 = 12 = 1
∴ The area of unit square = 1 unit2 or 1 square unit
Now, let us calculate the surface area of a unit cube.
Surface Area of a Cube in Square Units
We know that a unit cube has 6 faces, and the dimension of each side is 1 unit. Also, each of its faces is square in shape.
So, the area of each face = Side x Side
= 1 unit x 1 unit
= 1 square unit
Now, we know that the cube has 6 faces and a unit cube has all its 6 faces of 1 square unit each.
Therefore, the total surface area of the unit cube becomes:
6 x area of one face of a unit square, which is:
= 6 x 1 square unit
= 6 square units
Thus, the surface of the unit cube is 6 square units.
Do You Know?
A unit square has all its sides equal with a 90-degree angle at each vertex. Below, you can find the image of a unit square:
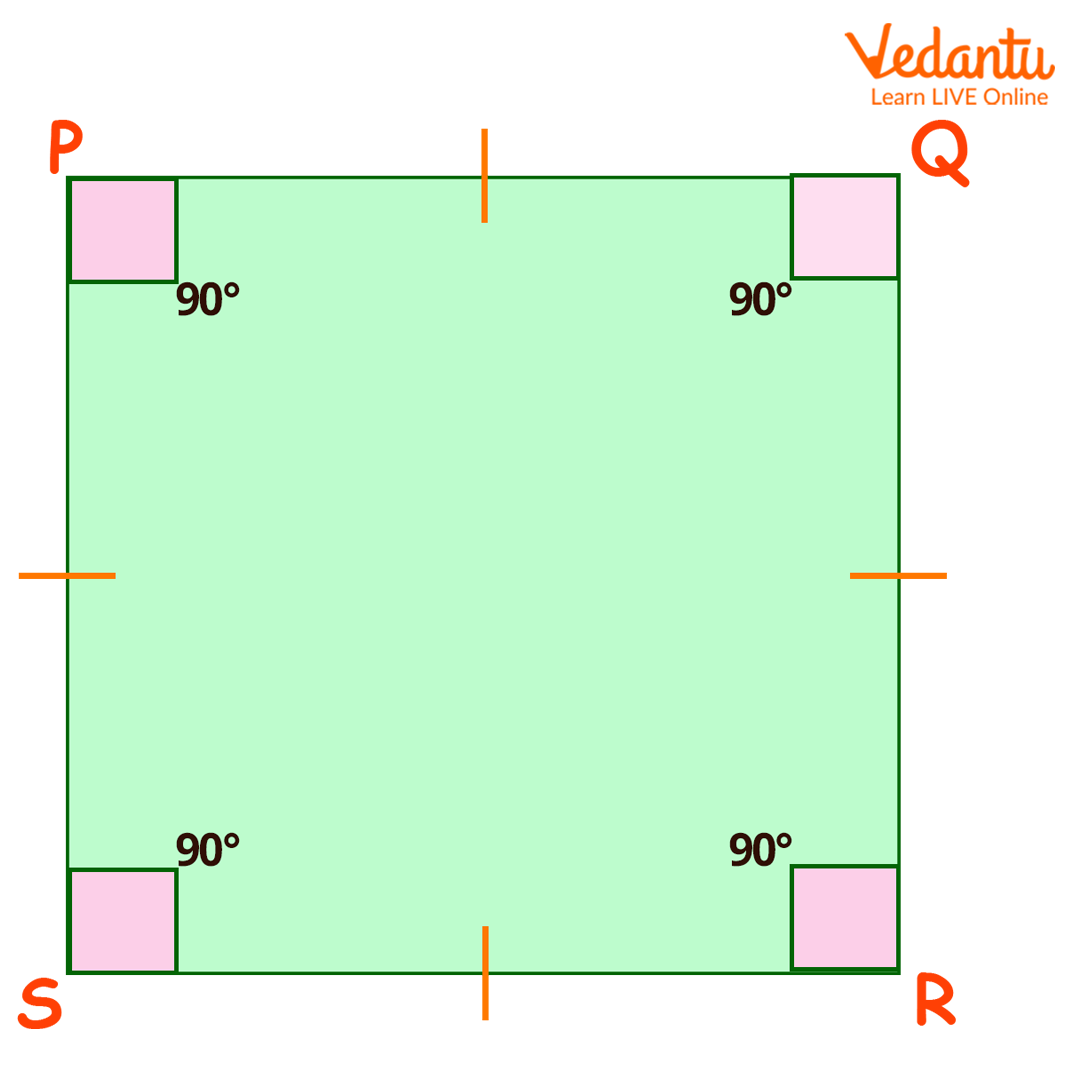
Square will all its 90-degree angles
The perimeter of a square is 2a. If the side is given as ‘a’. Also, the diagonal of a square is calculated as √2a. Therefore, unit square has side as ‘1’, perimeter as 2 and diagonal as √2.
From the above text on unit square definition, we understand that a square has all four sides equal with a magnitude of ‘a’, unlike other squares, a unit square has all four sides as ‘1’, so its area is also ‘1’ unit square.
FAQs on Unit Square - Definition, Formulas, and Facts
1. State eight properties of a square.
Properties of a square are as follows:
The diagonals bisect each other and meet at 90°.
The diagonals of a square bisect its angles.
Its opposite sides are both parallel and equal in length (magnitude).
All four angles of a square are equal (each having 360°/4 = 90° degree angle).
All four sides of a square are equal.
Opposite sides of a square are parallel.
Adding all four internal angles of a square, we get 360 degrees.
A square has 4 lines of reflectional symmetry.
2. How many faces does a unit square have?
A unit square does not have faces because it is a two-dimensional polygon. Such polygons are recognised by sides and angles only.









