Introduction To Three Dimensional Geometry Questions and Answers - Free PDF Download
In NCERT Solutions Class 11 Maths Chapter 11 Miscellaneous Exercise, you'll dive into the world of three-dimensional geometry! This chapter helps you learn how to find locations of points in 3D space, work with lines and planes, and understand the basics of direction ratios and cosines. If you get stuck on concepts or find 3D questions tricky, Vedantu’s step-by-step solutions will make things much easier to understand.
Table of Content
You’ll also come across important topics like finding midpoints, centroids, and applying formulas to solve higher-order problems. These NCERT solutions are available as free, downloadable PDFs so you can practice any time—even without the internet. If you want to check what’s included in the syllabus, the Class 11 Maths Syllabus has all the details.
Practicing with these solutions will boost your confidence and sharpen your 3D geometry skills for exams. Start with the exercises, and if you need more help, you can always use the detailed Class 11 Maths NCERT Solutions for every chapter.
Miscellaneous Exercise
1. Three vertices of a parallelogram $\text{ABCD}$ are $\text{A}\left( \text{3,-1,2} \right)$, $\text{B}\left( \text{1,2,-4} \right)$ and $\text{C}\left( \text{-1,1,2} \right)$. Find the coordinates of the fourth vertex.
Ans: We are given the three vertices of a parallelogram $\text{ABCD}$ are $\text{A}\left( \text{3,-1,2} \right)$, $\text{B}\left( \text{1,2,-4} \right)$ and $\text{C}\left( \text{-1,1,2} \right)$.
Let the coordinates of the fourth vertex of the parallelogram $\text{ABCD}$ be $\text{D}\left( \text{x,y,z} \right)$.
According to the property of a parallelogram, the diagonals of the parallelogram bisect each other.
In this parallelogram $\text{ABCD}$, $\text{AC}$ and $\text{BD}$ at point $\text{O}$.
So,
$\text{Mid-point of AC = Mid-point of BD}$
$\left( \frac{\text{3-1}}{\text{2}},\text{ }\frac{\text{-1+1}}{\text{2}},\text{ }\frac{\text{2+2}}{\text{2}} \right)\text{ = }\left( \frac{\text{x+1}}{\text{2}},\text{ }\frac{\text{y+1}}{\text{2}},\text{ }\frac{\text{z-4}}{\text{2}} \right)$
$\left( \text{1,0,2} \right)\text{ = }\left( \frac{\text{x+1}}{\text{2}},\text{ }\frac{\text{y+1}}{\text{2}},\text{ }\frac{\text{z-4}}{\text{2}} \right)$
$\frac{\text{x+1}}{\text{2}}\text{ = 1}$
$\frac{\text{y+2}}{\text{2}}\text{ = 0}$
$\frac{\text{z-4}}{\text{2}}\text{ = 2}$
We get, $\text{x = 1}$, $\text{y = 2}$ and $\text{z = 8}$
Therefore, the coordinates of the fourth vertex of the parallelogram $\text{ABCD}$ are $\text{D}\left( \text{1,-2,8} \right)$.
2. Find the lengths of the medians of the triangle with $\text{A}\left( \text{0,0,6} \right)$, $\text{B}\left( \text{0,4,0} \right)$ and $\text{C}\left( \text{6,0,0} \right)$.
Ans: For the given triangle $\text{ABC}$. Let $\text{AD}$, $\text{BE}$ and $\text{CF}$ are the medians:
We know that the median divides the line segment into two equal parts, so $\text{D}$ is the midpoint of $\text{BC}$, therefore,
$\text{Coordinates of point D = }\left( \frac{\text{0+6}}{\text{2}},\text{ }\frac{\text{4+0}}{\text{2}},\text{ }\frac{\text{0+0}}{\text{2}} \right)$
$\text{Coordinates of point D = }\left( \text{3,2,0} \right)$
$\text{AD = }\sqrt{{{\left( \text{0-3} \right)}^{\text{2}}}\text{+}{{\left( \text{0-2} \right)}^{\text{2}}}\text{+}{{\left( \text{6-0} \right)}^{\text{2}}}}$
$\text{AD = }\sqrt{\text{9+4+36}}$
$\text{AD = }\sqrt{\text{49}}$
$\text{AD = 7}$
Similarly, $\text{E}$ is the midpoint of $\text{AC}$,
$\text{Coordinates of point E = }\left( \frac{\text{0+6}}{\text{2}},\text{ }\frac{\text{0+0}}{\text{2}},\text{ }\frac{\text{0+6}}{\text{2}} \right)$
$\text{Coordinates of point E = }\left( \text{3,0,3} \right)$
$\text{AC = }\sqrt{{{\left( \text{3-0} \right)}^{\text{2}}}\text{+}{{\left( \text{0-4} \right)}^{\text{2}}}\text{+}{{\left( \text{3-0} \right)}^{\text{2}}}}$
$\text{AC = }\sqrt{\text{9+16+9}}$
$\text{AC = }\sqrt{\text{34}}$
Similarly, $\text{F}$ is the midpoint of $\text{AB}$,
$\text{Coordinates of point F = }\left( \frac{\text{0+0}}{\text{2}},\text{ }\frac{\text{0+4}}{\text{2}},\text{ }\frac{\text{6+0}}{\text{2}} \right)$
$\text{Coordinates of point F = }\left( \text{0,2,3} \right)$
$\text{CF = }\sqrt{{{\left( \text{6-0} \right)}^{\text{2}}}\text{+}{{\left( \text{0-2} \right)}^{\text{2}}}\text{+}{{\left( \text{0-3} \right)}^{\text{2}}}}$
$\text{CF = }\sqrt{\text{36+4+9}}$
$\text{CF = }\sqrt{\text{49}}$
$\text{CF = 7}$
Therefore, the lengths of the medians of the triangle $\text{ABC}$ we obtain are, $\text{7, }\sqrt{\text{34}}\text{, 7}$
3. If the origin is the centroid of the triangle $\text{PQR}$ with vertices $\text{P}\left( \text{2a,2,6} \right)$, $\text{Q}\left( \text{-4,3b,-10} \right)$ and $\text{R}\left( \text{8,14,2c} \right)$, then find the values of $\text{a}$, $\text{b}$ and $\text{c}$
Ans: The given triangle $\text{PQR}$
We know that the coordinates of the centroid of triangle with the vertices $\left( {{\text{x}}_{1}},{{\text{y}}_{1}},{{\text{z}}_{1}} \right)$, $\left( {{\text{x}}_{2}},{{\text{y}}_{2}},{{\text{z}}_{2}} \right)$ and $\left( {{\text{x}}_{3}},{{\text{y}}_{3}},{{\text{z}}_{3}} \right)$ are,
$\frac{{{\text{x}}_{\text{1}}}\text{+}{{\text{x}}_{\text{2}}}\text{+}{{\text{x}}_{\text{3}}}}{\text{3}}=\frac{{{\text{y}}_{\text{1}}}\text{+}{{\text{y}}_{\text{2}}}\text{+}{{\text{y}}_{\text{3}}}}{\text{3}}=\frac{{{\text{z}}_{\text{1}}}\text{+}{{\text{z}}_{\text{2}}}\text{+}{{\text{z}}_{\text{3}}}}{\text{3}}$
For triangle $\text{PQR}$, the coordinates will be,
$\text{ }\!\!\Delta\!\!\text{ PQR = }\frac{\text{2a-4+8}}{\text{3}}=\frac{\text{2+3b+14}}{\text{3}}=\frac{\text{6-10+2c}}{\text{3}}$
$\text{ }\!\!\Delta\!\!\text{ PQR = }\frac{\text{2a+4}}{\text{3}}=\frac{\text{3b+16}}{\text{3}}=\frac{\text{2c-4}}{\text{3}}$
Now, we are given that centroid is the origin,
$\frac{\text{2a+4}}{\text{3}}\text{ = 0}$
$\frac{\text{3b+16}}{\text{3}}\text{ = 0}$
$\frac{\text{2c-4}}{\text{3}}\text{ = 0}$
$\text{a = -2}$,
$\text{b = -}\frac{\text{16}}{\text{3}}$
$\text{c = 2}$
Therefore, we obtain the values as $\text{a = -2}$, $\text{b = -}\frac{\text{16}}{\text{3}}$ and $\text{c = 2}$.
4. If $\text{A}$ and $\text{B}$ be the points $\left( \text{3,4,5} \right)$ and $\left( \text{-1,3,-7} \right)$ respectively, find the equation of the set of points $\text{P}$ such that $\text{P}{{\text{A}}^{\text{2}}}\text{+P}{{\text{B}}^{\text{2}}}\text{ = }{{\text{k}}^{\text{2}}}$, where $\text{k}$ is a constant.
Ans: Let the coordinates of point $\text{P}$ be $\left( \text{x,y,z} \right)$.
Using the distance formula we get,
$\text{P}{{\text{A}}^{\text{2}}}\text{=}{{\left( \text{x-3} \right)}^{\text{2}}}\text{+}{{\left( \text{y-4} \right)}^{\text{2}}}\text{+}{{\left( \text{z-5} \right)}^{\text{2}}}$
$\text{P}{{\text{A}}^{\text{2}}}\text{ = }{{\text{x}}^{\text{2}}}\text{+9-6x+}{{\text{y}}^{\text{2}}}\text{+16-8y+}{{\text{z}}^{\text{2}}}\text{+25-10z}$
$\text{P}{{\text{A}}^{\text{2}}}\text{ = }{{\text{x}}^{\text{2}}}\text{-6x+}{{\text{y}}^{\text{2}}}\text{-8y+}{{\text{z}}^{\text{2}}}\text{-10z+50}$
Similarly,
$\text{P}{{\text{B}}^{\text{2}}}\text{ = }{{\left( \text{x-1} \right)}^{\text{2}}}\text{+}{{\left( \text{y-3} \right)}^{\text{2}}}\text{+}{{\left( \text{z-7} \right)}^{\text{2}}}$
$\text{P}{{\text{A}}^{\text{2}}}\text{ = }{{\text{x}}^{\text{2}}}\text{-2x+}{{\text{y}}^{\text{2}}}\text{-6y+}{{\text{z}}^{\text{2}}}\text{-14z+59}$
We are given that,
$\text{P}{{\text{A}}^{\text{2}}}\text{+P}{{\text{B}}^{\text{2}}}\text{ = }{{\text{k}}^{\text{2}}}$
So,
$\left( {{\text{x}}^{\text{2}}}\text{-6x+}{{\text{y}}^{\text{2}}}\text{-8y+}{{\text{z}}^{\text{2}}}\text{-10z+50} \right)\text{+}\left( {{\text{x}}^{\text{2}}}\text{-2x+}{{\text{y}}^{\text{2}}}\text{-6y+}{{\text{z}}^{\text{2}}}\text{-14z+59} \right)\text{ = }{{\text{k}}^{2}}$
$\text{2}{{\text{x}}^{\text{2}}}\text{+2}{{\text{y}}^{\text{2}}}\text{+2}{{\text{z}}^{\text{2}}}\text{-4x-14y+14z+109 =}\ {{\text{k}}^{\text{2}}}$
$\text{2}\left( {{\text{x}}^{\text{2}}}\text{+}{{\text{y}}^{\text{2}}}\text{+}{{\text{z}}^{\text{2}}}\text{-2x-7y+7z} \right)\text{ = }{{\text{k}}^{\text{2}}}\text{-109}$
${{\text{x}}^{\text{2}}}\text{+}{{\text{y}}^{\text{2}}}\text{+}{{\text{z}}^{\text{2}}}\text{-2x-7y+7z = }\frac{{{\text{k}}^{\text{2}}}\text{-109}}{\text{2}}$
Therefore, the equation is as follows ${{\text{x}}^{\text{2}}}\text{+}{{\text{y}}^{\text{2}}}\text{+}{{\text{z}}^{\text{2}}}\text{-2x-7y+2z = }\frac{{{\text{k}}^{\text{2}}}\text{-109}}{\text{2}}$
Conclusion
NCERT Solutions for Miscellaneous Exercise Class 11 Chapter 11 helps in understanding three-dimensional geometry. The Miscellaneous Exercise includes different types of problems that improve skills in 3D geometry. Practising these problems is important for doing well in exams and for future studies in Maths. These exercises help students gain confidence and become better at solving complex geometry questions.
Class 11 Maths Chapter 11: Exercises Breakdown
CBSE Class 11 Maths Chapter 11 Other Study Materials
Chapter-Specific NCERT Solutions for Class 11 Maths
Given below are the chapter-wise NCERT Solutions for Class 11 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Important Related Links for CBSE Class 11 Maths
FAQs on NCERT Solutions For Class 11 Maths Miscellaneous Exercise Chapter 11 Introduction To Three Dimensional Geometry - 2025-26
1. Is the distance formula for three-dimensional geometry completely different from the 2D formula?
No, the 3D distance formula is a direct and logical extension of the 2D Pythagorean theorem, simply adding the z-coordinate's contribution. Students often feel it's a new concept, but the underlying principle remains the same.
Think of it as finding the diagonal of a rectangular box. In 2D, the distance between (x₁, y₁) and (x₂, y₂) is √( (x₂-x₁)² + (y₂-y₁)² ). In 3D, you just add the 'height' component.
2. Do the miscellaneous exercise solutions for 3D Geometry just provide the final answer?
The NCERT Solutions for the Class 11 Maths Chapter 11 miscellaneous exercise provide detailed, step-by-step derivations for every problem, not just the final answers. The misconception arises from thinking of them as simple answer keys.
Each solution is designed to explain the 'how' and 'why' behind the answer.
3. For a point on the YZ-plane, are the y and z coordinates zero?
No, for any point lying on the YZ-plane, its x-coordinate is always zero. The confusion often comes from mixing up planes and axes. For a point to be on the YZ-plane, it has moved zero units along the x-axis, so its coordinates are (0, y, z).
4. Is the section formula in Class 11 3D Geometry a completely new concept?
No, the section formula in three-dimensional geometry is a straightforward extension of the formula you learned for 2D coordinate geometry. The core logic of dividing a line segment in a specific ratio remains identical.
5. Are the Class 11 Maths Chapter 11 miscellaneous exercise solutions free to download?
Yes, the solutions are available as a Free PDF download, which you can access and use offline without any cost. Many students believe that high-quality, step-by-step educational resources require payment, but these NCERT solutions are provided to support free learning for all.
6. How are octants numbered in 3D geometry? Is it random?
The eight octants in 3D geometry are numbered based on a systematic sign convention for the (x, y, z) coordinates, not randomly. This system is a logical extension of the four quadrants in a 2D Cartesian plane.
7. Is it okay to use solutions for the Miscellaneous Exercise of Class 11 Chapter 3D Geometry, or is it just for cheating?
Using NCERT solutions for self-assessment after you have genuinely attempted the problems is a smart learning strategy, not cheating. The purpose is to verify your method, understand different approaches, and correct your mistakes, which helps in better retention and exam performance.
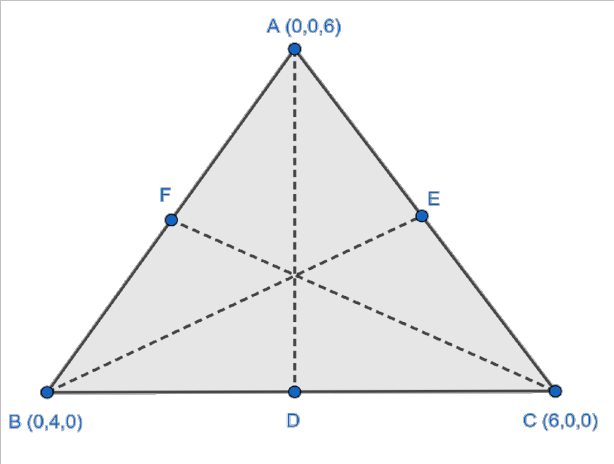
8. Does the centroid formula for a triangle in 3D space only work for specific triangles?
No, the formula for finding the centroid of a triangle works for any type of triangle in 3D space (scalene, isosceles, right-angled, etc.). It is a general formula derived by averaging the coordinates of the vertices: C = ((x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3, (z₁+z₂+z₃)/3).
9. Do the Class 11 Maths Chapter 11 miscellaneous exercise solutions only help with that specific exercise?
No, working through the miscellaneous exercise solutions provides a comprehensive revision of the entire chapter. The questions in this section are designed to be application-based, integrating multiple concepts learned earlier.
A common myth is that these solutions are isolated from the main chapter content. However, a single miscellaneous problem might require you to use both the distance formula and the section formula, or apply properties of geometric shapes like parallelograms or right-angled triangles in a 3D context.
By solving these complex problems, you strengthen your understanding of core principles.
10. Are online solutions for the miscellaneous exercise of Chapter 11 always updated for the current NCERT book?
Yes, reliable academic platforms like Vedantu ensure that their NCERT solutions are meticulously aligned with the latest NCERT syllabus and textbook editions. This guarantees that every question from your current textbook's miscellaneous exercise is covered accurately, preventing confusion from outdated or mismatched content.
11. Where is a point like (0, 0, 5) located in a 3D plane?
A point with coordinates (0, 0, z) where z is a non-zero number lies on the z-axis, not the origin or a plane. The misconception arises from associating zero coordinates with the origin alone.
The origin is a unique point with coordinates (0, 0, 0). If only the x and y coordinates are zero, it means the point has not moved along the x or y direction from the origin; it has only moved along the z-axis.
