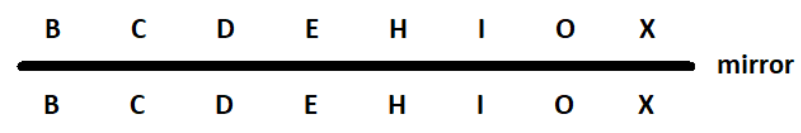Class 7 Maths Chapter 12 Questions and Answers - Free PDF Download
Exercise 12.1
1. Copy the figures with punched holes and find the axes of symmetry for the following:
(a).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(b).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(c).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(d).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(e).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(f).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(g).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(h).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(i).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(j).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(k).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
(l).
Ans: The axes of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The axes of symmetry in the given figure will be,
2. Given the line(s) of symmetry, find the other hole(s):
(a).
Ans: The axes or lines of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The other hole in the given figure along the line of symmetry will be,
(b).
Ans: The axes or lines of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The other hole in the given figure along the line of symmetry will be,
(c).
Ans: The axes or lines of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The other hole in the given figure along the line of symmetry will be,
(d).
Ans: The axes or lines of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The other hole in the given figure along the line of symmetry will be,
(e).
Ans: The axes or lines of symmetry are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The other hole in the given figure along the line of symmetry will be,
3. In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure by performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you completed?
(a).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
The name of the completed figure is square.
(b).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
The name of the completed figure is triangle.
(c).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
The name of the completed figure is rhombus.
(d).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
The name of the completed figure is circle.
(e).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
The name of the completed figure is pentagon.
(f).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
The name of the completed figure is octagon.
4. The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
Identify multiple lines of symmetry, if any, in each of the following figures:
(a).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The multiple lines of symmetry in the given figure are as follows,
(b).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The multiple lines of symmetry in the given figure are as follows,
(c).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The multiple lines of symmetry in the given figure are as follows,
(d).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The multiple lines of symmetry in the given figure are as follows,
(e).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The multiple lines of symmetry in the given figure are as follows,
(f).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The multiple lines of symmetry in the given figure are as follows,
(g).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The multiple lines of symmetry in the given figure are as follows,
(h).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The multiple lines of symmetry in the given figure are as follows,
5. Copy the figure given here: Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
On taking one diagonal as the line of symmetry and shading a few more squares to make the figure symmetric about the diagonal, we obtain the following figure,
(image will be uploaded soon)
On taking one diagonal as the line of symmetry and shading a few more squares to make the figure symmetric about the diagonal, we obtain the following figure,
Therefore, we can conclude that there is more than one way to make the figure symmetric about the diagonal. Also, we can see that the figure obtained is symmetric about both the diagonals.
6. Copy the diagram and complete each shape to be symmetric about the mirror line(s):
(a).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
(b).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
(c).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
(d).
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
The completed figure after performing the reflection along the dotted mirror line is as follows,
7. State the number of lines of symmetry for the following figures:
(a). An equilateral triangle
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw an equilateral triangle. Draw all the possible lines of symmetry for the equilateral triangle.
There are three lines of symmetry in an equilateral triangle.
(b). An isosceles triangle
The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw an isosceles triangle. Draw all the possible lines of symmetry for the isosceles triangle.
There is only one line of symmetry.
(c). A scalene triangle
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw a scalene triangle. Draw all the possible lines of symmetry for the scalene triangle.
There is only no line of symmetry.
(d). A square
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw a square. Draw all the possible lines of symmetry for the square.
There are four lines of symmetry.
(e). A rectangle
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw a rectangle. Draw all the possible lines of symmetry for the rectangle.
There are two lines of symmetry.
(f). A rhombus
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw a rhombus. Draw all the possible lines of symmetry for the rhombus.
There are two lines of symmetry.
(g). A parallelogram
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw a parallelogram. Draw all the possible lines of symmetry for the parallelogram.
There are no lines of symmetry.
(h). A quadrilateral
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw a quadrilateral. Draw all the possible lines of symmetry for the quadrilateral.
There are no lines of symmetry.
(i). A regular hexagon
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw a regular hexagon. Draw all the possible lines of symmetry for the regular hexagon.
There are six lines of symmetry.
(j). A circle
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Draw a circle. Draw all the possible lines of symmetry for the circle.
There are infinite lines of symmetry.
8. What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about:
(a). A Vertical Mirror
Ans: Reflectional symmetry is the symmetry that is caused by the reflections of the mirror. The mirror is placed in different positions like vertically or horizontally to check the reflections and determine whether they are symmetrical or not.
We will place the mirror vertically and check for all the alphabets. On checking, the following alphabets were obtained that were the reflections on the mirror.
(ii) A Horizontal Mirror
Ans: Reflectional symmetry is the symmetry that is caused by the reflections of the mirror. The mirror is placed in different positions like vertically or horizontally to check the reflections and determine whether they are symmetrical or not.
We will place the mirror horizontally and check for all the alphabets. On checking, the following alphabets were obtained that were the reflections on the mirror.
(iii) Both Horizontal and Vertical Mirrors
Ans: Reflectional symmetry is the symmetry that is caused by the reflections of the mirror. The mirror is placed in different positions like vertically or horizontally to check the reflections and determine whether they are symmetrical or not.
The alphabets that possess both vertical and horizontal reflections can be determined by placing the mirror once vertically and then horizontally and bringing out the common alphabets from both the cases.
We will place the mirror vertically and check for all the alphabets. On checking the following alphabets were obtained that were the reflections on the mirror.
We will place the mirror horizontally and check for all the alphabets. On checking the following alphabets were obtained that were the reflections on the mirror.
From the above two cases we can determine the alphabets that are common for both the vertical and the horizontal reflections.
These alphabets are H, I, O, and X.
9. Give three examples of shapes with no line of symmetry.
The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
Examples of three shapes that have no lines of symmetry are as follows,
A Scalene Triangle
A scalene triangle has no lines of symmetry.
A Quadrilateral
A quadrilateral has no lines of symmetry.
A Parallelogram
A parallelogram has no lines of symmetry.
10. What other name can you give to the line of symmetry of:
(i) An Isosceles Triangle?
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
An isosceles triangle has two equal sides.
There is only one line of symmetry. This line of symmetry is also known as the median or the altitude of the triangle.
(ii) A Circle?
Ans: The axes or lines of symmetry or the mirror lines are the lines that divide any figure into two equal halves which look exactly like one another. A figure can have more than one axes of symmetry.
There are infinite lines of symmetry. This line of symmetry is also known as the diameter of the circle.
What will you learn in Class 7 Maths Chapter 12 Exercise 12.1 solutions of Vedantu?
Vedantu’s solutions are extremely easy to understand and creates an impact on the minds of the students. If you are a student of Class 7 CBSE board, then you must start studying from the Vedantu’s solutions.
Vedantu’s solutions contain all the topics of the Class 7 Maths Chapter 12.1 and provide you with a clear and concise idea of the different concepts that are taught in the chapter.
Contents of the CBSE Class 7 Chapter 12 Maths Exercise 12.1
CBSE Class 7 Maths Exercise 12.1 consists of the following topics:
Symmetry and its types
Different shapes
Centre of Rotation
Order of Rotation
Angle of Rotation
The questions that you will get answers to in the solution of Vedantu Class 7 Maths Chapter 12.1 are as follow:
State the numbers of the lines of symmetry in various figures
What letters of the English alphabet have reflectional symmetry?
What name can you give to the line of symmetry of different shapes ( isosceles triangle, circle, etc)?
Give examples of shapes with no lines of symmetry.
Other questions related to diagrams.
Why Should You Refer To the Solutions of Vedantu to Study Maths Exercise 12.1 Class 7?
Vedantu’s solutions on Maths Exercise 12.1 Class 7 consists of all the information related to the concept of Symmetry. Once you start studying from the solutions of Vedantu, you will have a better understanding of the entire chapter. Now you will learn better thus scoring high marks in the examination. The solutions od Vedantu are properly provided to you with the help of diagrams and effective representations.
You will be able yo remember the solutions better, thus you will save time while writing the answers in your answer sheets during the examination. The solutions are highly effective for both your school examination and other competitive examination in the future. The solutions are written in a simple and easy manner for enhancing the process of revision.
The solutions are coupled with better tips and tricks, helping students score high marks. These tricks can help a student reach the top of the marks list in examination by simply helping them solve the maths problems in a much better and impressive manner.
The PDFs are provided to students for free. You can download them on your PCs or laptops by just visiting the website of Vedantu. Or you can also download NCERT Solutions Class 7 Maths Chapter 12 Exercise 12.1 PDF crafted by Vedantu on your mobile phones. All you need to do is download the Vedantu app.
Why Vedantu?
Vedantu is the one-stop solution for all your exam preparation needs. It’s the best online tutor that you can ever come across. The solutions of Vedantu are prepared by highly qualified teachers and professors who have been teaching students of the CBSE board for many years.
They know what exactly the students lack. Everyone wants to get high scores, but either they don’t get time to revise all topics or they don’t get the time to revise all the topics before exams.
The NCERT Solutions for Class 7 Maths Chapter 12 Exercise 12.1 is prepared with proficiency to help students learn anything is the least time possible. The solutions are written in the most captivating manner to make sure that the interest of students grows on the subject effectively.
Once you start studying the NCERT Solutions for Class 7 Maths Chapter 12 ex 12.1 you will get to learn all the concepts of the chapter in a simple manner, without much hassle and effort. Vedantu makes the process of learning and revising easier for you. You will see the difference yourself once you start referring to the solutions of Vedantu. All you need to do is go through the solutions of Vedantu once or twice and then write them on your once. That’s it and you are absolutely prepared with the chapter for your upcoming examination. Download the PDF of Vedantu on Class 7 Maths Chapter 12 ex 12.1 and kickstart your preparation for the upcoming examination.
Class 7 Maths Chapter 12: Exercises Breakdown
CBSE Class 7 Maths Chapter 12 Other Study Materials
Chapter-Specific NCERT Solutions for Class 7 Maths
Given below are the chapter-wise NCERT Solutions for Class 7 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Important Related Links for NCERT Class 7 Maths
Access these essential links for NCERT Class 7 Maths, offering comprehensive solutions, study guides, and additional resources to help students master language concepts and excel in their exams.
FAQs on NCERT Solutions For Class 7 Maths Chapter 12 Symmetry Exercise 12.1 - 2025-26
1. Where can I find reliable, step-by-step NCERT Solutions for Class 7 Maths Chapter 12, Symmetry, for the 2025-26 session?
You can find detailed and accurate NCERT Solutions for Class 7 Maths Chapter 12 (Symmetry) on Vedantu. These solutions are crafted by subject experts and provide a step-by-step breakdown for every question in all exercises, strictly following the CBSE 2025-26 syllabus and guidelines.
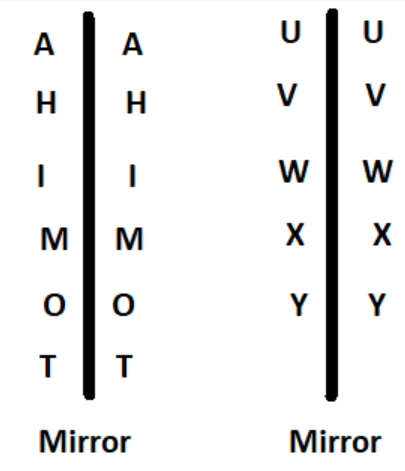
2. What is the correct method to solve questions on identifying lines of symmetry in Exercise 12.1?
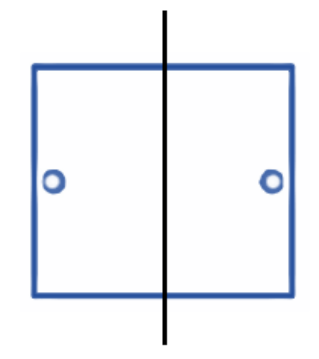
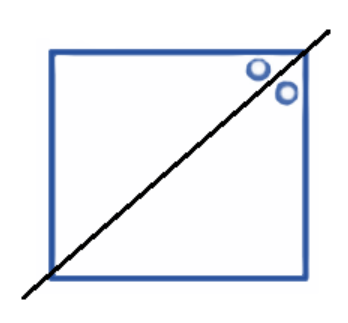
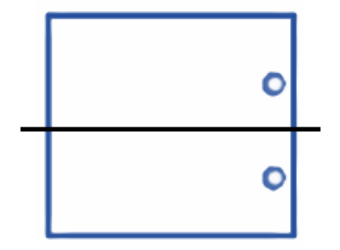
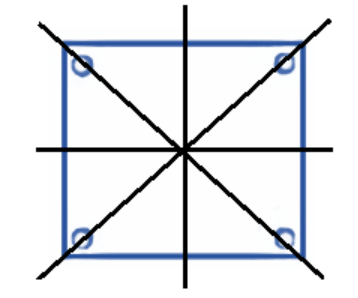
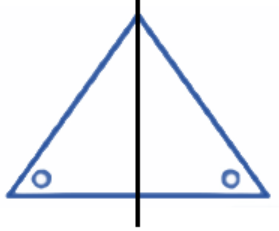
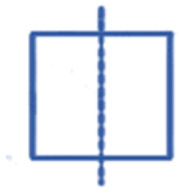
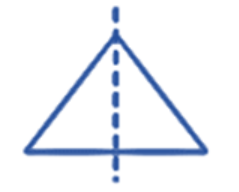
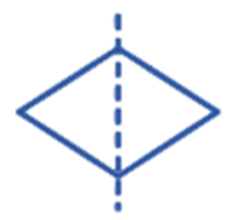
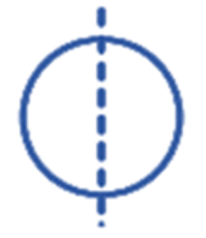
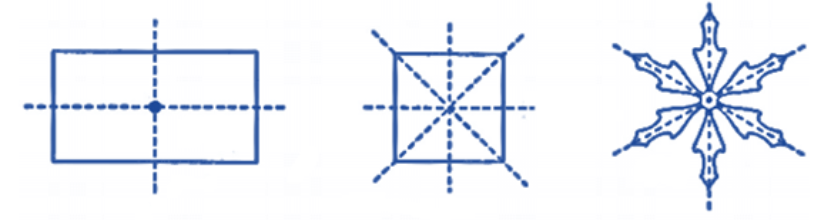
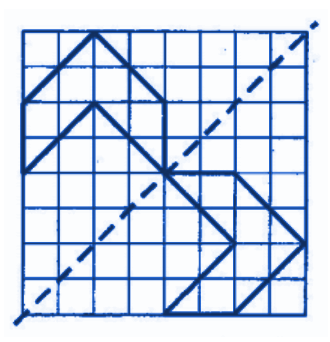
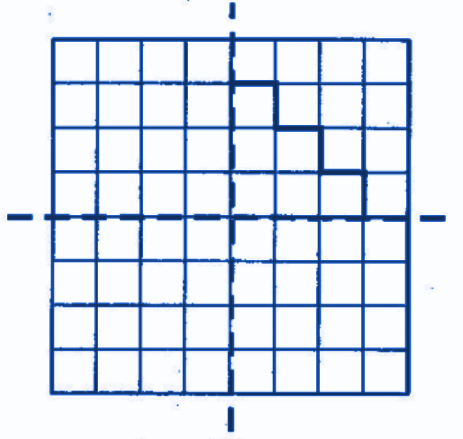
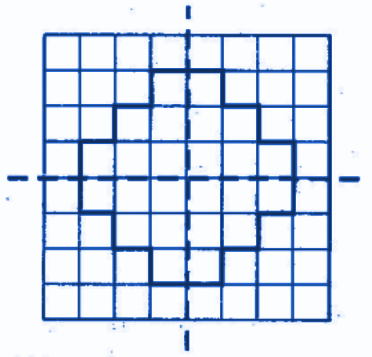
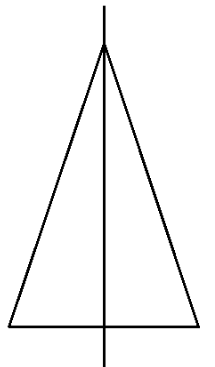
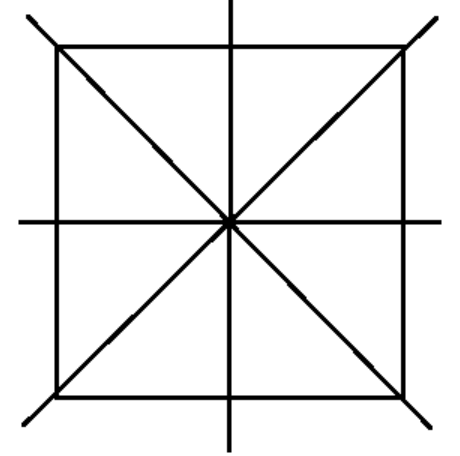
The correct method, as demonstrated in the NCERT solutions, is to first draw the given figure. Then, you need to identify all possible lines along which the figure can be folded so that the two halves perfectly overlap. For a regular polygon, the number of lines of symmetry is equal to the number of sides. For example, a square has 4 lines of symmetry.
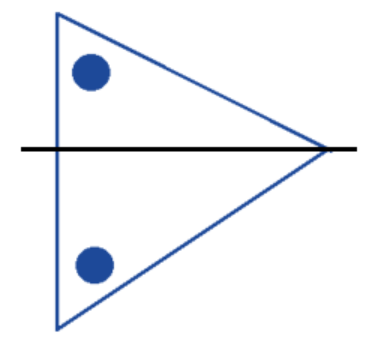
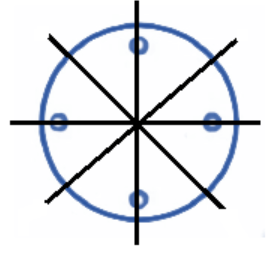
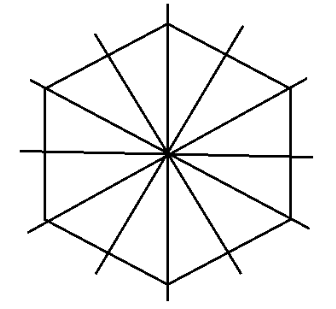
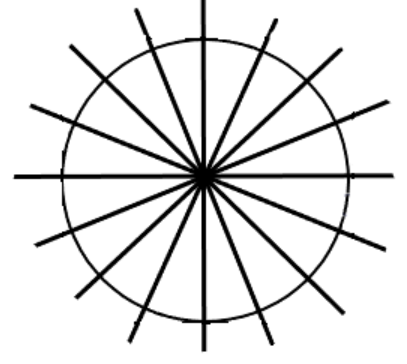
3. How do the NCERT Solutions for Class 7 Maths Chapter 12 explain the concept of rotational symmetry covered in Exercise 12.2?
The solutions explain rotational symmetry by focusing on three key elements:
- Centre of Rotation: The fixed point around which the figure turns.
- Angle of Rotation: The minimum angle the figure must be turned to look exactly the same as its original position.
- Order of Rotation: The number of times a figure fits onto itself during a full 360° rotation. The solutions provide clear diagrams to illustrate this for each problem.
4. What types of problems are included in NCERT Solutions for Chapter 12, Exercise 12.3?
Exercise 12.3 focuses on identifying shapes that have both line symmetry and rotational symmetry. The solutions guide you on how to check for both properties in a single figure. You will solve problems that require you to name quadrilaterals or other shapes that meet specific criteria for both types of symmetry.
5. Why is it important to follow the step-by-step method from NCERT solutions when finding the order of rotational symmetry?
Following the step-by-step method is crucial for accuracy. It ensures you correctly identify the centre of rotation first, which is the most critical step. Systematically rotating the figure (e.g., by 90°, 120°) helps you count the number of times it aligns with its original position without missing any instance. This methodical approach prevents miscalculation and builds a strong conceptual understanding as per the CBSE pattern.
6. How do NCERT solutions help differentiate between a shape with no symmetry and one with a rotational symmetry of order 1?
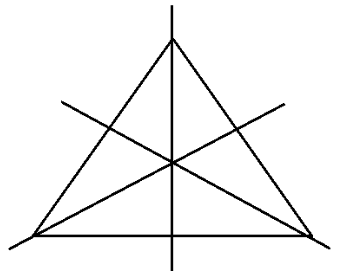
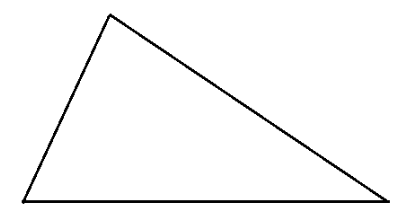
The NCERT solutions clarify that these are essentially the same. A shape with a rotational symmetry of order 1 only fits onto itself after a complete 360° turn. This means it has no rotational symmetry in a practical sense. For example, a scalene triangle has an order of rotational symmetry of 1, and the solutions classify it as a shape with no rotational symmetry.
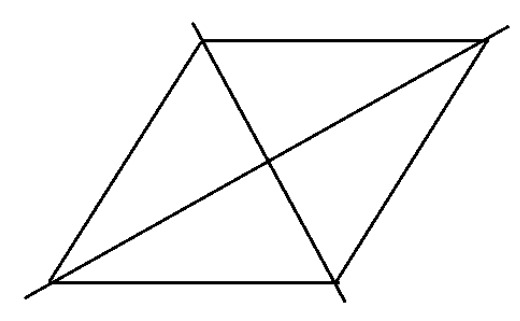
7. How does the solution for a parallelogram's symmetry in Chapter 12 differ from that of a rectangle?
The NCERT solutions clearly distinguish them:
- A parallelogram has no lines of symmetry but possesses rotational symmetry of order 2 about the intersection point of its diagonals.
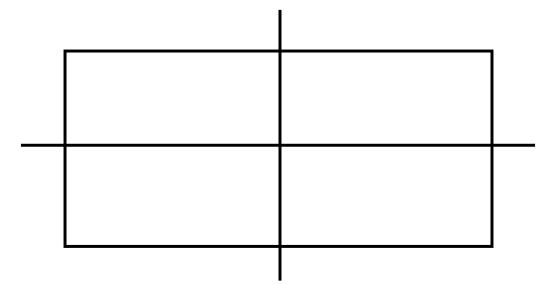
- A rectangle, on the other hand, has two lines of symmetry (joining the mid-points of opposite sides) and also has rotational symmetry of order 2. This comparison helps clarify that rotational symmetry can exist without line symmetry.
8. According to the method in NCERT solutions, how can you determine if a shape has both line and rotational symmetry?
The correct procedure is to first check for lines of symmetry by drawing and testing mirror-image folds. If a figure has two or more lines of symmetry, the solutions explain that it will automatically have rotational symmetry. The point where these lines intersect becomes the centre of rotation. This rule helps solve problems in Exercise 12.3 efficiently.
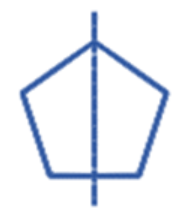
9. How do you solve a problem that asks to find the angle of rotation for a regular pentagon?
As per the NCERT solutions, the method is as follows:
1. First, identify the order of rotational symmetry. For a regular pentagon, the order is 5 (equal to its number of sides).
2. The total angle in a full turn is 360°.
3. To find the angle of rotation, divide the total angle by the order of symmetry: 360° / 5 = 72°. Therefore, the angle of rotation is 72°.
