NCERT Solutions for Class 7 Maths Chapter 12 (EX 12.3)
Exercise 12.3
1. Name any two figures that have both line symmetry and rotational symmetry.
Ans: The line symmetry is the symmetry that is caused along a line. This line is known as the axes of symmetry or the lines of symmetry. They are the lines that divide any figure into two equal halves which look exactly like one another. A figure might have at least one axis of symmetry.
Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure.
Two figures that have both line symmetry and rotational symmetry are as follows,
i. An Equilateral Triangle
An equilateral triangle possesses both line and rotational symmetry.
The line symmetry is as follows,
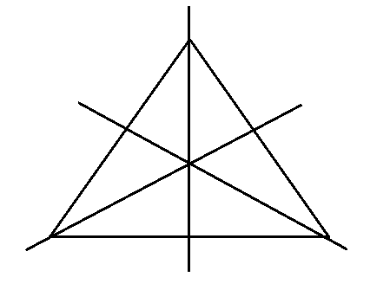
There are three lines of symmetry in an equilateral triangle.
The rotational symmetry is as follows,
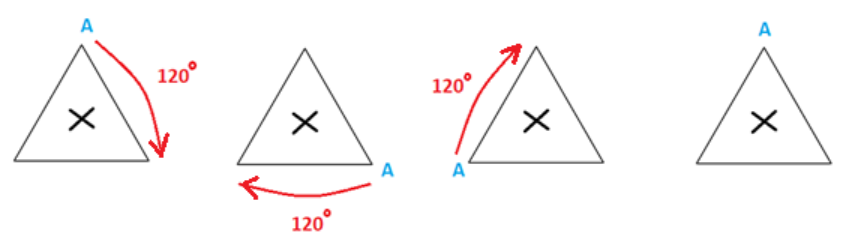
The given figure can be rotated three times at $120^\circ $ angles each to produce the symmetrical figures.
Therefore, the order of rotational symmetry for the above figure is 3.
ii. A circle
A circle possesses both line and rotational symmetry.
The line symmetry is as follows,
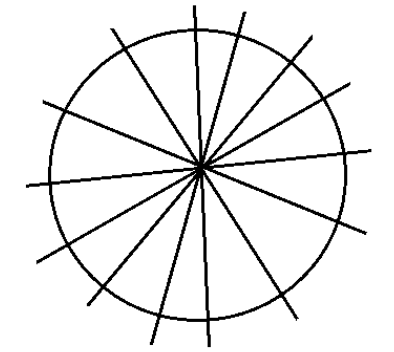
The circle also possesses rotational symmetry. This is because when it is rotated about the center point at any angle, it will return back the same figure which is the circle.
2. Draw, wherever possible, a rough sketch of:
i. A triangle with both line and rotational symmetries of order more than 1.
Ans: The line symmetry is the symmetry that is caused along a line. This line is known as the axes of symmetry or the lines of symmetry. They are the lines that divide any figure into two equal halves which look exactly like one another. A figure might have at least one axis of symmetry.
Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure.
An equilateral triangle has both line and rotational symmetries of order more than 1.
The line symmetry is as follows,
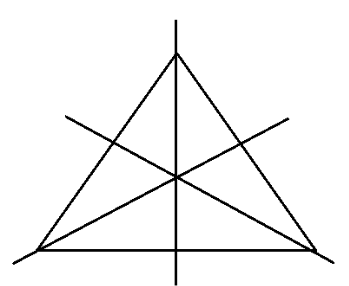
There are three lines of symmetry in an equilateral triangle.
The rotational symmetry is as follows,
The given figure can be rotated three times at $120^\circ $ angles each to produce the symmetrical figures.
Therefore, the order of rotational symmetry for the above figure is 3.
ii. A triangle with only line symmetry and no rotational symmetry of order more than 1.
Ans: The line symmetry is the symmetry that is caused along a line. This line is known as the axes of symmetry or the lines of symmetry. They are the lines that divide any figure into two equal halves which look exactly like one another. A figure might have at least one axis of symmetry.
Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure. A triangle with only line symmetry and no rotational symmetry of order more than 1 is an isosceles triangle.
The line symmetry is as follows,
(The rotational symmetry is as follows,
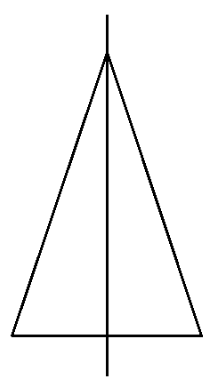
There is only one line of symmetry.
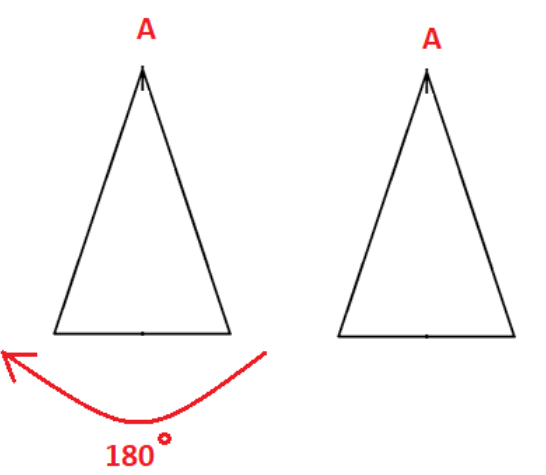
There is no rotational symmetry of order more than 1. This is because we will get the original figure back only when we will rotate it $360^\circ $.
iii. A quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
Ans: The line symmetry is the symmetry that is caused along a line. This line is known as the axes of symmetry or the lines of symmetry. They are the lines that divide any figure into two equal halves which look exactly like one another. A figure might have at least one axis of symmetry.
Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure.
We have to find a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
The above stated case is not possible. This is because if the order of rotational symmetry is more than 1 for any figure, then the figure will always have a line of symmetry.
iv. A quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Ans: The line symmetry is the symmetry that is caused along a line. This line is known as the axes of symmetry or the lines of symmetry. They are the lines that divide any figure into two equal halves which look exactly like one another. A figure might have at least one axis of symmetry.
Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure.
A Quadrilateral with line symmetry and not rotational symmetry of order more than 1 is an isosceles trapezium.
The line symmetry is as follows,
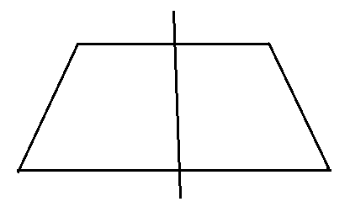
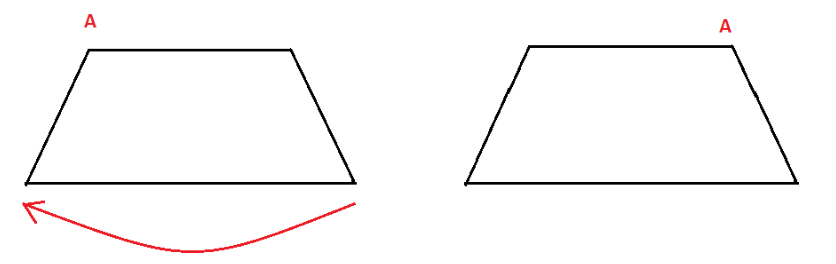
There is only one line of symmetry. And there is no rotational symmetry of order more than 1. This is because we will get the original figure back only when we will rotate it $360^\circ $.
3. If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Ans: The line symmetry is the symmetry that is caused along a line. This line is known as the axes of symmetry or the lines of symmetry. They are the lines that divide any figure into two equal halves which look exactly like one another. A figure might have at least one axis of symmetry.
Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure.
If a figure has at least two lines of symmetry, then it has rotational symmetry of order more than 1. This is because every line that passes through the center forms a line of symmetry. And these lines of symmetry form the rotational symmetry around the center. The rotational symmetry is formed for every angle that is subtended at the center.
4. Fill in the blanks:
Ans: The completed table is as follows,
5. Name the quadrilateral which has both line and rotational symmetry of order more than 1.
Ans: The line symmetry is the symmetry that is caused along a line. This line is known as the axes of symmetry or the lines of symmetry. They are the lines that divide any figure into two equal halves which look exactly like one another. A figure might have at least one axis of symmetry.
Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure.
A quadrilateral that has both line and rotational symmetry of order more than 1 is a square.
The line symmetry is as follows,
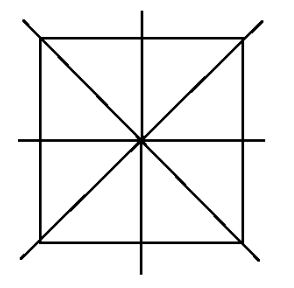
There are four lines of symmetry.
The rotational symmetry is as follows,
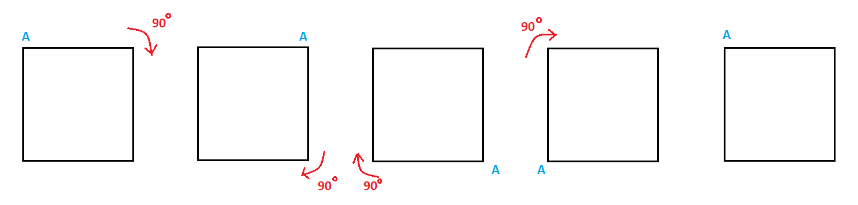
The given figure can be rotated four times at $90^\circ $ angles each to produce the symmetrical figures.
Therefore, the order of rotational symmetry for the above figure is four.
6. After rotating by $60^\circ $ about the centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
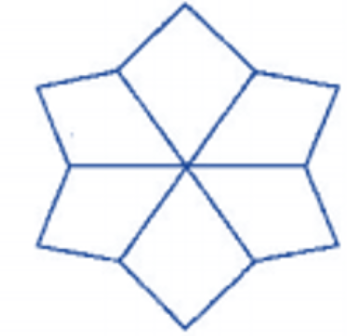
Ans: Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure.
Order of rotational symmetry is the number of times a figure can be rotated $360^\circ $ to produce the similar figures.
The given figure looks the same as its original position when it is rotated by $60^\circ $ about the centre.
The rotation for $60^\circ $ is given as follows,
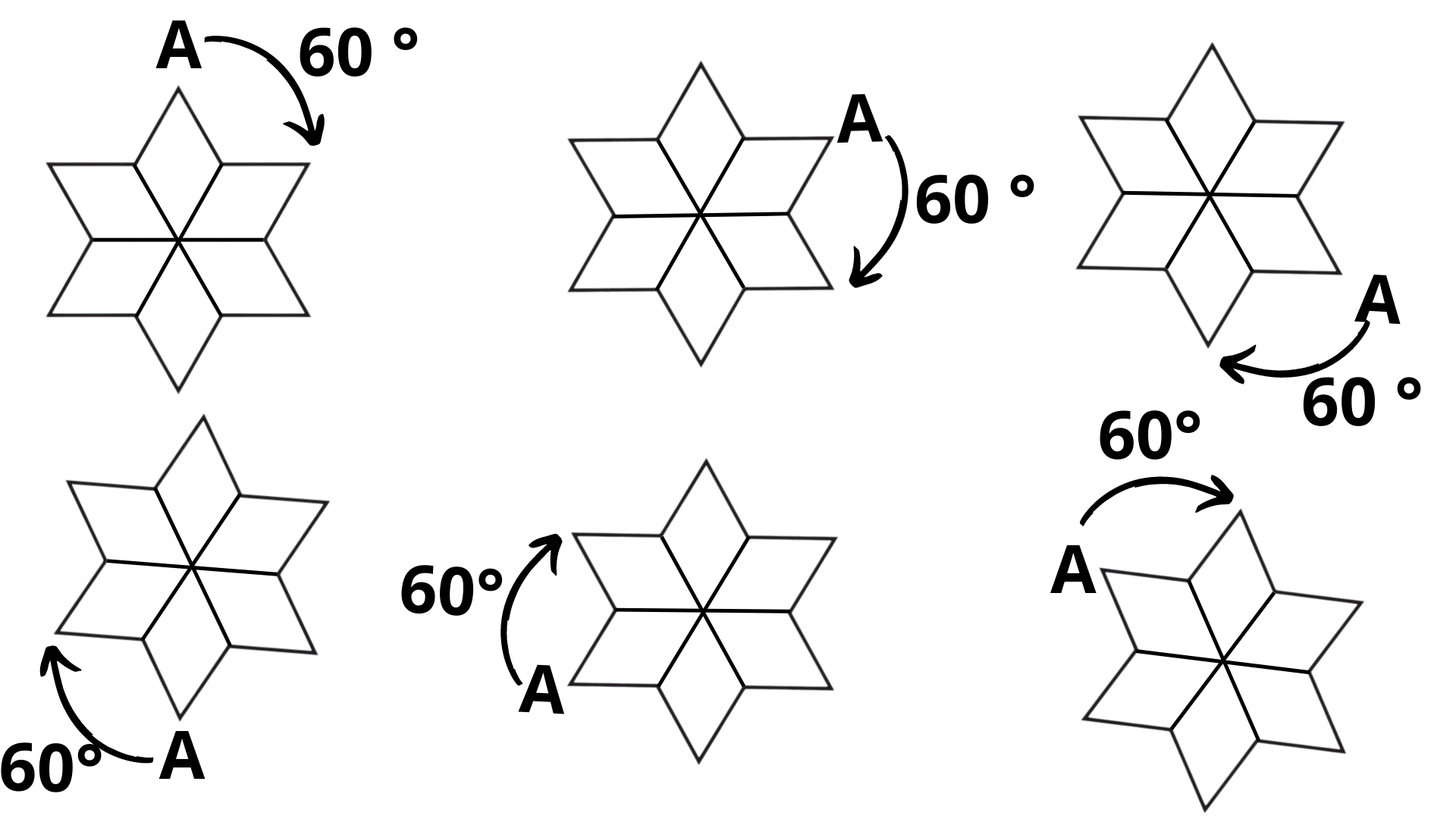
The figure rotates six times to produce symmetrical shapes at $60^\circ $.
The other angles at which we will obtain the symmetrical figures are as follows,
The figure will rotate at $120^\circ $.
The rotation for $120^\circ $ is given as follows,
The figure rotates six times to produce symmetrical shapes at $120^\circ $.
The figure will rotate at $180^\circ $.
The rotation for $180^\circ $ is given as follows,
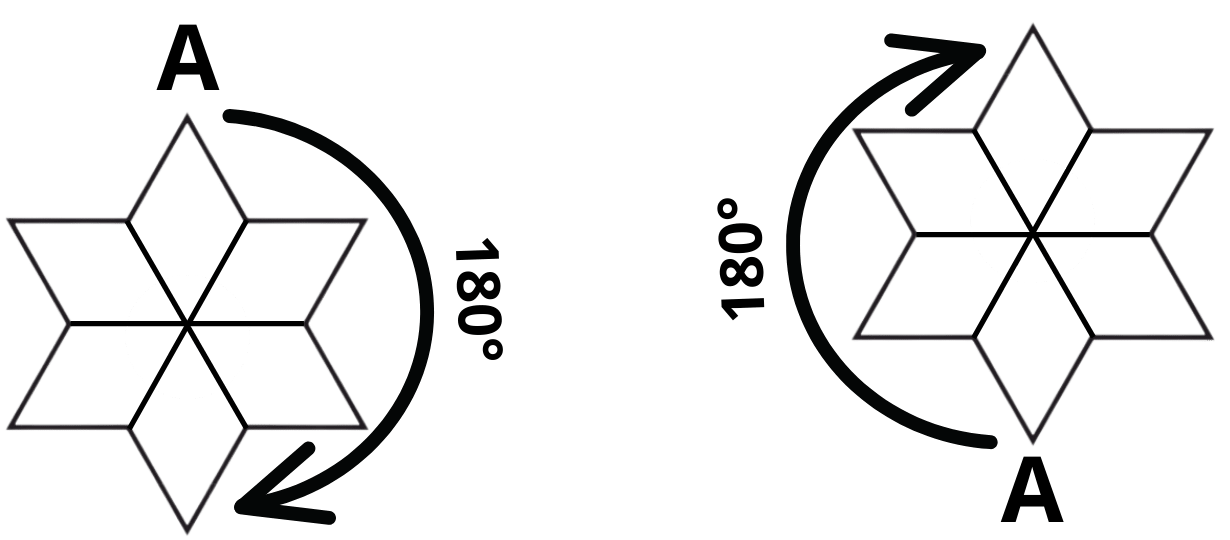
The figure rotates two times to produce symmetrical shapes at $180^\circ $.
The figure will rotate at $360^\circ $.
The rotation for $360^\circ $ is given as follows,
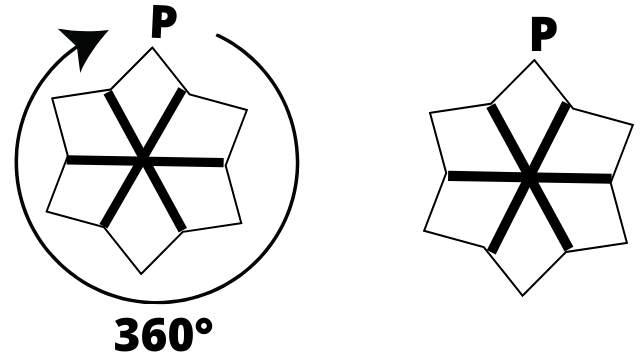
The figure rotates one time to produce symmetrical shapes at $360^\circ $.
Some other angles at which the given figure can rotate are $240^\circ $, $300^\circ $ and so on.
7. Can we have a rotational symmetry of order more than 1 whose angle of rotation is:
i. $45^\circ $
Ans: Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure. Order of rotational symmetry is the number of times a figure can be rotated $360^\circ $ to produce the similar figures. Order of symmetry can be calculated by dividing $360^\circ $ by the measure of the given angle.
On dividing $360^\circ $ by $45^\circ $, we get,
$\dfrac{{360^\circ }}{{45^\circ }} = 8$
Therefore, if the angle of rotation is $45^\circ $ then the symmetry of order is possible. This is because we obtain a whole number of divisions. Also, the order of rotation would be 8.
ii. $17^\circ $
Ans: Rotational symmetry or radial symmetry is the symmetry which is caused when an object, if rotated about its own axis, gives back the same figure. Order of rotational symmetry is the number of times a figure can be rotated $360^\circ $ to produce the similar figures. Order of symmetry can be calculated by dividing $360^\circ $ by the measure of the given angle.
On dividing $360^\circ $ by $17^\circ $, we get,
$\dfrac{{360^\circ }}{{17^\circ }} = 22.18^\circ $
Therefore, if the angle of rotation is $17^\circ $ then the symmetry of order is not possible. This is because we do not obtain a whole number of divisions.
NCERT Solutions for Class 7 Maths Chapter 12 Symmetry Exercise 12.3
Opting for the NCERT solutions for Ex 12.3 Class 7 Maths is considered as the best option for the CBSE students when it comes to exam preparation. This chapter consists of many exercises. Out of which we have provided the Exercise 12.3 Class 7 Maths NCERT solutions on this page in PDF format. You can download this solution as per your convenience or you can study it directly from our website/ app online.
Vedantu in-house subject matter experts have solved the problems/ questions from the exercise with the utmost care and by following all the guidelines by CBSE. Class 7 students who are thorough with all the concepts from the Maths textbook and quite well-versed with all the problems from the exercises given in it, then any student can easily score the highest possible marks in the final exam. With the help of this Class 7 Maths Chapter 12 Exercise 12.3 solutions, students can easily understand the pattern of questions that can be asked in the exam from this chapter and also learn the marks weightage of the chapter. So that they can prepare themselves accordingly for the final exam.
Besides these NCERT solutions for Class 7 Maths Chapter 12 Exercise 12.3, there are plenty of exercises in this chapter which contain innumerable questions as well. All these questions are solved/answered by our in-house subject experts as mentioned earlier. Hence all of these are bound to be of superior quality and anyone can refer to these during the time of exam preparation. In order to score the best possible marks in the class, it is really important to understand all the concepts of the textbooks and solve the problems from the exercises given next to it.
Do not delay any more. Download the NCERT solutions for Class 7 Maths Chapter 12 Exercise 12.3 from Vedantu website now for better exam preparation. If you have the Vedantu app in your phone, you can download the same through the app as well. The best part of these solutions is these can be accessed both online and offline as well.
Class 7 Maths Chapter 12: Exercises Breakdown
CBSE Class 7 Maths Chapter 12 Other Study Materials
Chapter-Specific NCERT Solutions for Class 7 Maths
Given below are the chapter-wise NCERT Solutions for Class 7 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Important Related Links for NCERT Class 7 Maths
Access these essential links for NCERT Class 7 Maths, offering comprehensive solutions, study guides, and additional resources to help students master language concepts and excel in their exams.
