NCERT Solutions For Class 7 Maths Chapter 12 Algebraic Expressions in Hindi - 2025-26
FAQs on NCERT Solutions For Class 7 Maths in Hindi Chapter 12 Algebraic Expressions (2025-26)
1. Where can I find accurate, step-by-step NCERT Solutions for Class 7 Maths Chapter 12 (Algebraic Expressions) for the 2025-26 session?
You can find detailed and accurate NCERT Solutions for Class 7 Maths Chapter 12 on Vedantu's platform. These solutions are prepared by subject matter experts and provide a step-by-step guide to solving every problem in the textbook. They are fully aligned with the latest CBSE 2025-26 syllabus, ensuring you understand the correct methods to answer questions in your exams.
2. What is the correct method for adding two algebraic expressions, for example, (7x + 5y) and (2x - 3y), as per the NCERT textbook?
According to the method in the NCERT textbook, you should add algebraic expressions by combining like terms. Here is the step-by-step process for the example:
Step 1: Write the expressions to be added: (7x + 5y) + (2x - 3y).
Step 2: Group the like terms together. Like terms are those that have the same variables raised to the same power. Here, group the 'x' terms and the 'y' terms: (7x + 2x) + (5y - 3y).
Step 3: Add or subtract the coefficients of the like terms: (7+2)x + (5-3)y.
Step 4: Simplify to get the final answer: 9x + 2y.
3. How do I find the value of an algebraic expression like 3a + 5b - 2 when a=2 and b=1?
To find the value of an algebraic expression for given values of variables, you need to substitute the values into the expression and then simplify. The NCERT Solutions explain this method as follows:
Step 1: Start with the given expression: 3a + 5b - 2.
Step 2: Substitute the given values for each variable. Replace 'a' with 2 and 'b' with 1: 3(2) + 5(1) - 2.
Step 3: Perform the multiplication first: 6 + 5 - 2.
Step 4: Perform the addition and subtraction from left to right: 11 - 2 = 9. Therefore, the value of the expression is 9.
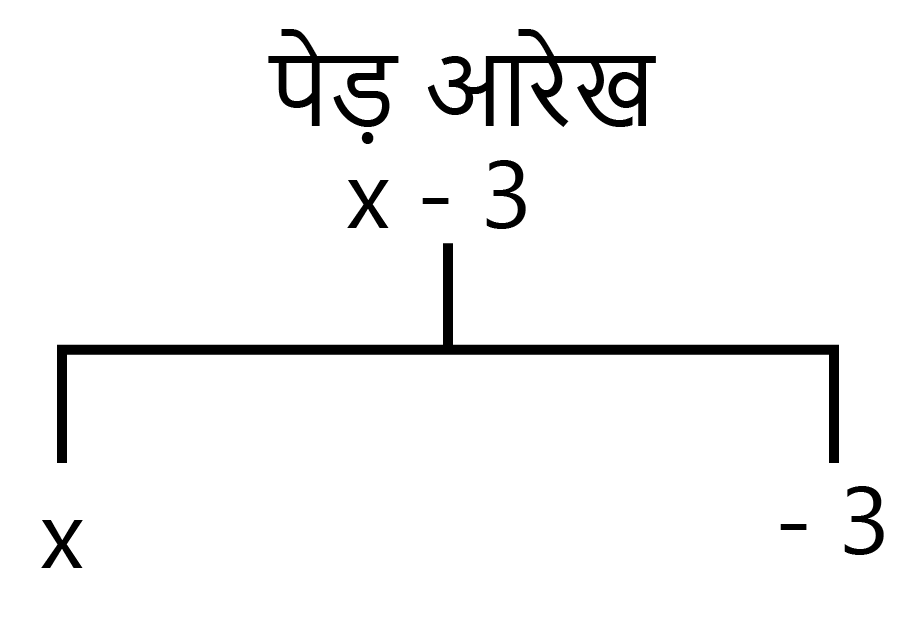
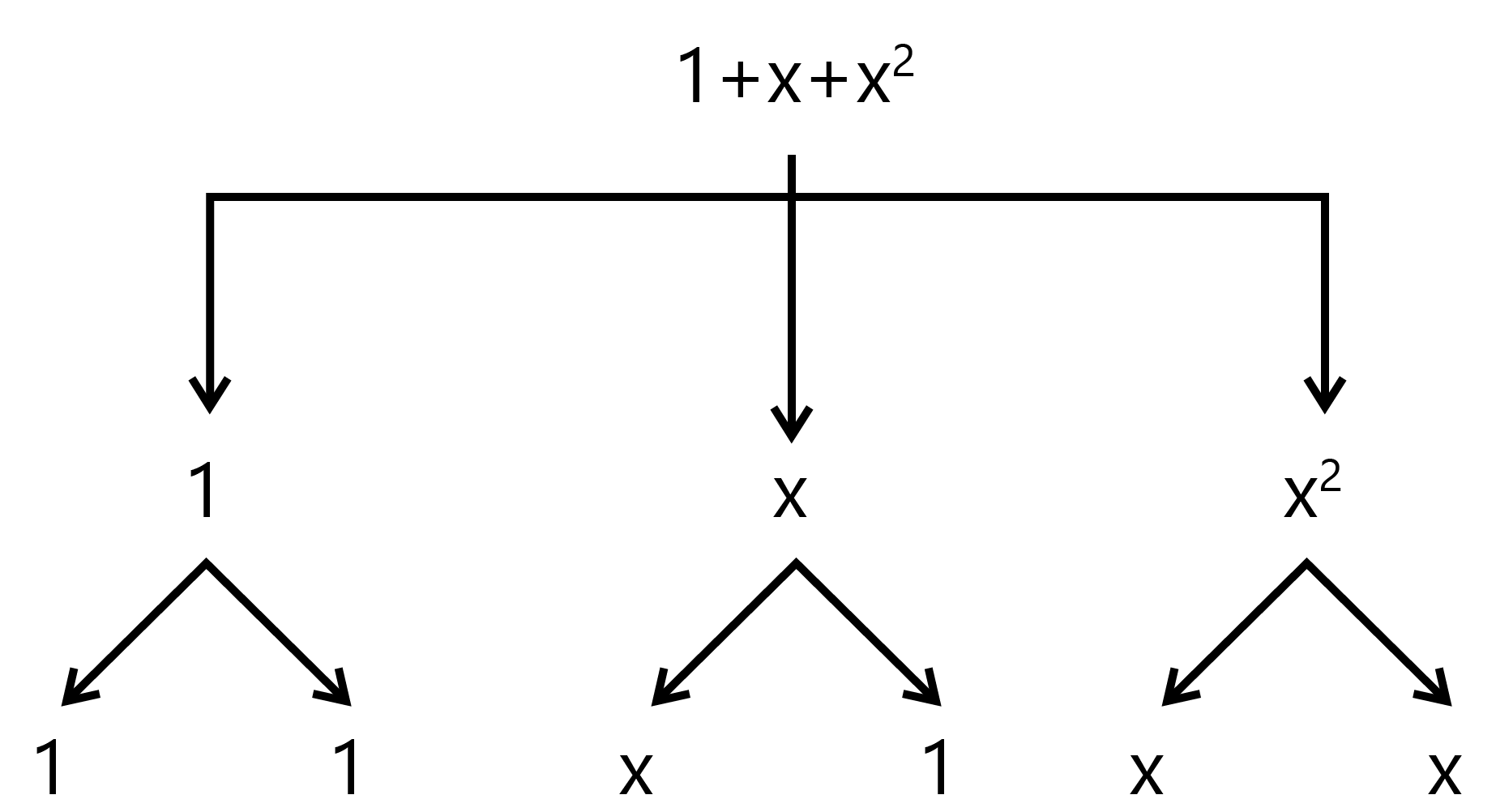
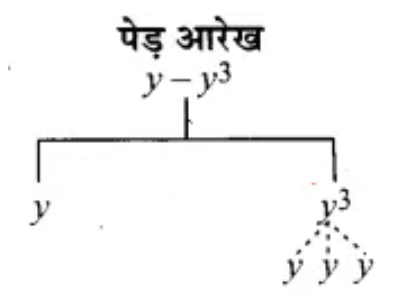
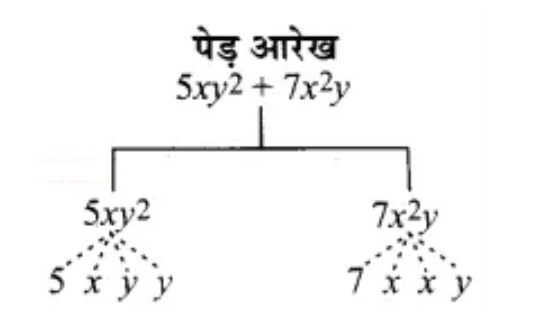
4. What is the difference between a term and a coefficient in an algebraic expression, with an example from Chapter 12?
In an algebraic expression, terms are the individual parts of the expression that are separated by addition (+) or subtraction (-) signs. The coefficient is the numerical factor of a term. For example, in the expression 8xy - 5x:
- The terms are 8xy and -5x.
- In the term 8xy, the coefficient is 8.
- In the term -5x, the coefficient is -5.
5. Why is it crucial to identify and group 'like terms' before performing addition or subtraction in algebraic expressions?
It is crucial to group like terms because addition and subtraction are only possible for terms that represent the same type of quantity. Think of variables as objects: '3x' could represent 3 apples and '4y' could represent 4 bananas. You can't add them to get '7xy' (7 apple-bananas). However, if you have '3x' (3 apples) and '2x' (2 apples), you can combine them to get '5x' (5 apples). Grouping like terms (e.g., all 'x' terms together, all 'y' terms together) ensures you are combining only those quantities that can be mathematically combined, which is the fundamental rule for simplifying expressions.
6. What is a common mistake students make when subtracting one algebraic expression from another, for instance, subtracting (a - b) from (2a + b)?
A very common mistake is forgetting to change the sign of every term in the expression being subtracted. When subtracting (a - b) from (2a + b), the correct setup is (2a + b) - (a - b). The critical step is to apply the negative sign to both 'a' and '-b'. The expression becomes 2a + b - a - (-b), which simplifies to 2a + b - a + b. Many students incorrectly write 2a + b - a - b, forgetting to change -b to +b. The correct answer after combining like terms is a + 2b.
7. How do the NCERT Solutions for Chapter 12 explain the classification of polynomials based on the number of terms?
The NCERT Solutions explain that polynomials can be classified based on how many non-zero terms they contain:
A monomial is an expression with only one term (e.g., 7x, or 4y²).
A binomial is an expression with two unlike terms (e.g., 2a + 3b, or x² - 4).
A trinomial is an expression with three unlike terms (e.g., x + y + 7, or a² + 2ab + b²).
An expression with more than one term with non-zero coefficients and variables having non-negative integral exponents is generally called a polynomial.
8. How does understanding algebraic expressions in Chapter 12 help in solving practical problems?
Understanding algebraic expressions is a foundational skill in mathematics because it allows us to translate real-world problems into a mathematical format that can be solved. For instance, if you want to calculate the perimeter of a rectangle whose length is 5 units more than its width ('w'), you can express the length as w + 5. The perimeter can then be written as the algebraic expression 2(w + (w+5)). By simplifying this expression to 4w + 10, you create a general formula to find the perimeter for any given width. This skill is essential for building formulas and solving word problems in geometry, finance, and science.