NCERT Solutions Class 7 Maths Exercise 2.1 Solutions for Chapter 2: Fractions and Decimals

1. Which of the drawings (a) to (d ) show: 

(i) $2 \times \dfrac{1}{5} $ 

(ii) $2 \times \dfrac{1}{2} $

(iii) $3 \times \dfrac{2}{3}$   

(iv) $3 \times \dfrac{1}{4}$

(a)

(b)

(c)

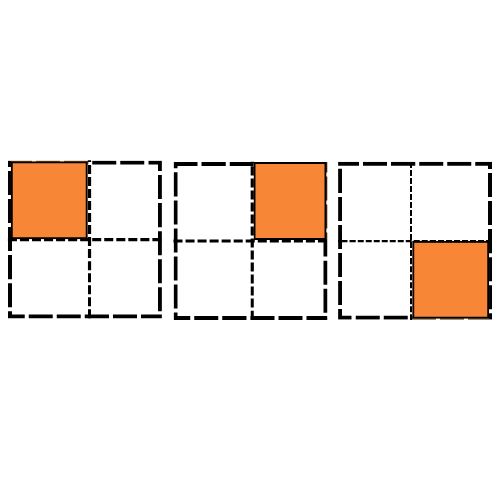
(d)

Ans:

(i) Given: $2 \times \dfrac{1}{5} $

We need to find which figure represent  the above expression.

We can write it as  

$2 \times \dfrac{1}{5} = \dfrac{1}{5} + \dfrac{1}{5}$

Fig(d)  represents two figures in which each figure  have\[1\] shaded part out of \[5\] equal parts .

So, we have $\dfrac{1}{5}$shaded part from both figures.

$ \Rightarrow \dfrac{1}{5} + \dfrac{1}{5} = 2 \times \dfrac{1}{5} $

Hence, Fig (d) represents $2 \times \dfrac{1}{5} $.

(ii) Given: $2 \times \dfrac{1}{2} $

We need to find which figure represent  the above expression.

We can write it as  

$2 \times \dfrac{1}{2} = \dfrac{1}{2} + \dfrac{1}{2}$

Fig(b) represents two figures in which each figure have 1 shaded part out of 2 equal parts.

So, we have $\dfrac{1}{2}$ shaded part from both figures.

$ \Rightarrow \dfrac{1}{2} + \dfrac{1}{2} = 2 \times \dfrac{1}{2}$

Hence, Fig(b) represents $2 \times \dfrac{1}{2}$.

(iii) Given: $3 \times \dfrac{2}{3}$

We need to find which figure represent  the above expression.

We can write it as  

$3 \times \dfrac{2}{3} = \dfrac{2}{3} + \dfrac{2}{3} + \dfrac{2}{3}$

Fig(a)  represents three figures in which each figure have \[2\] shaded parts out of \[3\]equal  parts .

So, we have $\dfrac{2}{3}$ shaded part from each figure.

$ \Rightarrow \dfrac{2}{3} + \dfrac{2}{3} + \dfrac{2}{3} = 3 \times \dfrac{2}{3}$

Hence, Fig (a) represents $3 \times \dfrac{2}{3}$.

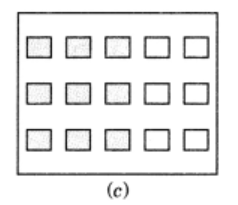
(iv) Given: $3 \times \dfrac{1}{4}$

We need to find which figure represent  the above expression.

We can write it as  

$3 \times \dfrac{1}{4} = \dfrac{1}{4} + \dfrac{1}{4} + \dfrac{1}{4}$

Fig(c)  represents three figures in which each figure have \[1\] shaded part out of \[4\] equal parts .

So, we have $\dfrac{1}{4}$ shaded part from each figure.

$ \Rightarrow \dfrac{1}{4} + \dfrac{1}{4} + \dfrac{1}{4} = 3 \times \dfrac{1}{4}$

Hence, Fig (c) represents $3 \times \dfrac{1}{4}$.

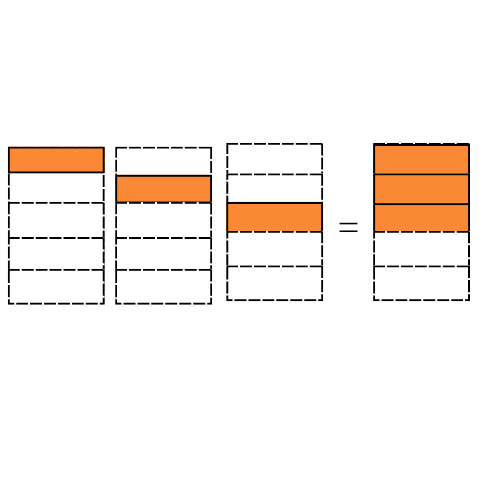
2. Some pictures (a) to (c) are given below. Tell which of them show:

(i)$3 \times \dfrac{1}{5} = \dfrac{3}{5}$         (ii) $2 \times \dfrac{1}{3} = \dfrac{2}{3}$       (iii) $3 \times \dfrac{3}{4} = 2\dfrac{1}{4}$

(a)

(b)

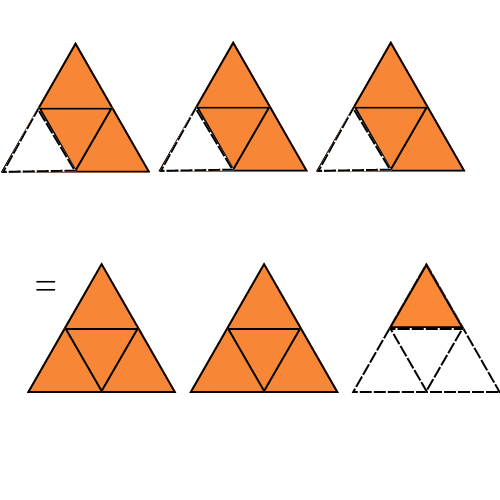
(c)

Ans: (i)Given:  $3 \times \dfrac{1}{5} = \dfrac{3}{5} $

We need to find which figure represent  the above expression.

We can write it as  

 $3 \times \dfrac{1}{5} = \dfrac{3}{5} = \dfrac{1}{5} + \dfrac{1}{5} + \dfrac{1}{5} $

Fig(c)  represents three figures in which each figure have  $1 $ shaded part out of  $5 $ equal parts .

So, we have $\dfrac{1}{5}$ shaded part from each figure.

 $ \Rightarrow \dfrac{1}{5} + \dfrac{1}{5} + \dfrac{1}{5} = 3 \times \dfrac{1}{5} = \dfrac{3}{5} $

Hence, Fig (c) represents  $3 \times \dfrac{1}{5} = \dfrac{3}{5} $.

(ii) Given:  $2 \times \dfrac{1}{3} = \dfrac{2}{3} $

We need to find which figure represent  the above expression.

We can write it as  

 $2 \times \dfrac{1}{3} = \dfrac{2}{3} = \dfrac{1}{3} + \dfrac{1}{3} $

Fig(a) represents two figures in which each figure have 1 shaded part out of  $3 $equal parts.

So, we have $\dfrac{1}{3} $ shaded part from both figures.

 $ \Rightarrow \dfrac{1}{3} + \dfrac{1}{3} = 2 \times \dfrac{1}{3} = \dfrac{2}{3} $

Hence, Fig(a) represents  $2 \times \dfrac{1}{3} = \dfrac{2}{3} $.

(iii) Given:  $3 \times \dfrac{3}{4} = 2\dfrac{1}{4} $

We need to find which figure represent  the above expression.

We can write it as  

 $ \Rightarrow 3 \times \dfrac{3}{4} = \dfrac{3}{4} + \dfrac{3}{4} + \dfrac{3}{4} $

Fig(b)  represents three figures in which each figure have  $3 $ shaded parts out of  $4 $ equal  parts .

So, we have $\dfrac{3}{4} $ shaded part from each figure.

 $ \Rightarrow \dfrac{3}{4} + \dfrac{3}{4} + \dfrac{3}{4} = 3 \times \dfrac{3}{4} $

Hence, Fig (b) represents  $3 \times \dfrac{3}{4} = 2\dfrac{1}{4} $.

3. Multiply and reduce to lowest form and convert into a mixed fraction:

(i)  $7 \times \dfrac{3}{5} $

Ans: Given:  $7 \times \dfrac{3}{5} $

We need to convert the given expression into a mixed fraction.

 Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $\Rightarrow 7 \times \dfrac{3}{5}  $ 

 $= (\dfrac{7}{1}) \times (\dfrac{3}{5}) $  

 $ = \dfrac{7 \times 3}{5 \times 1}$   

 $= \dfrac{21}{5}$   

 $= 4\dfrac{1}{5}  $  $ \text{(because multiplication of fraction rule)} $

(ii)  $4 \times \dfrac{1}{3} $

Ans: Given:  $4 \times \dfrac{1}{3} $

We need  to convert given expression  into mixed fraction.

Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $\Rightarrow 4 \times \dfrac{1}{3} $  

 $ = \dfrac{4 \times 1}{3}   $

 $= \dfrac{4}{3}   $

 $ = 1\dfrac{1}{3} $   $ \text{(because multiplication of fraction rule)} $

(iii)  $2 \times \dfrac{6}{7} $

Ans: Given:  $2 \times \dfrac{6}{7} $

We need  to convert given expression  into mixed fraction.

Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $\Rightarrow 2 \times \dfrac{6}{7} $  

  $ = \dfrac{{2 \times 6}}{7} $  

  $ = \dfrac{12}{7}   $

  $ = 1\dfrac{5}{7}   $ $ \text{(because multiplication of fraction rule)} $

(iv)  $5 \times \dfrac{2}{9} $

Ans: Given:  $5 \times \dfrac{2}{9} $

We need to convert the given expression into a mixed fraction.

Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $\Rightarrow 5 \times \dfrac{2}{9} $  

 $  = \dfrac{5 \times 2}{9}   $

  $ = \dfrac{10}{9}   $

  $ = 1\dfrac{1}{9}  $   $ \text{(because multiplication of fraction rule)} $

(v)  $\dfrac{2}{3} \times 4$

Ans: Given:  $\dfrac{2}{3} \times 4  $

We need  to convert given expression  into mixed fraction.

Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $ \Rightarrow \dfrac{2}{3} \times 4   $

   $= \dfrac{{2 \times 4}}{3} $ 

   $= \dfrac{8}{3}   $

  $ = 2\dfrac{2}{3}  $ $ \text{(because multiplication of fraction rule)} $

(vi)  $ \dfrac{5}{2} \times 6 $

Ans: Given:  $5 \times \dfrac{2}{6} $

We need to convert the given expression into a mixed fraction.

Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $\Rightarrow \dfrac{5}{2} \times 6$   

   $= 5 \times 3  $

   $ = 15 $  $ \text{(because multiplication of fraction rule)} $

(vii)  $11 \times \dfrac{4}{7} $

Ans: Given:  $11 \times \dfrac{4}{7} $

We need  to convert given expression  into mixed fraction.

Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $\Rightarrow 11 \times \dfrac{4}{7}  $ 

  $ = \dfrac{11 \times 4}{7} $  

   $= \dfrac{44}{7} $  

  $ = 6\dfrac{2}{7} $ $ \text{(because multiplication of fraction rule)} $

(viii)  $20 \times \dfrac{4}{5} $

Ans: Given:  $20 \times \dfrac{4}{5} $

We need  to convert given expression  into mixed fraction.

Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $\Rightarrow 20 \times \dfrac{4}{5}  $ 

   $= \dfrac{20 \times 4}{5}  $ 

  $ = 4 \times 4  $ 

  $ = 16 $ $ \text{(because multiplication of fraction rule)} $

(ix)  $13 \times \dfrac{1}{3} $

Ans: Given:  $13 \times \dfrac{1}{3} $

We need  to convert given expression  into mixed fraction.

Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $\Rightarrow 13 \times \dfrac{1}{3}  $ 

  $ = \dfrac{13 \times 1}{3}  $ 

  $= \dfrac{13}{3}$   

  $ = 4\dfrac{1}{3} $  $ \text{(because multiplication of fraction rule)} $

(x)  $15 \times \dfrac{3}{5} $

Ans: Given : $15 \times \dfrac{3}{5} $

We need  to convert given expression  into mixed fraction.

Multiplication of Fraction rule is given by

Product of fraction  $ =  $(product of numerator)/(product of denominator)

 $\Rightarrow 15 \times \dfrac{3}{5}$   

   $ = \dfrac{{15 \times 3}}{5}$    

   $ = 3 \times 3$ 

   $ = 9 $  $ \text{(because multiplication of fraction rule)} $

4. Shade:

(i) $\dfrac{1}{2}$

of the circles in box

(ii) $\dfrac{2}{3}$

of the triangles in box

(iii) $\dfrac{3}{5}$

of the squares in box                                                 

(a)

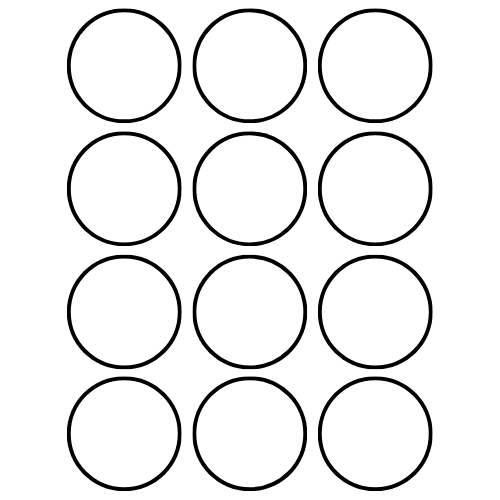
(b)

(c)

Ans:

(i) Given: \[12\] circles in the box.

We need to shade $\dfrac{1}{2}$of the circles in the box.

As we know , there are \[12\] circles in the box.

$ \Rightarrow \dfrac{1}{2}$ of the \[12\] circles

$= \dfrac{1}{2} \times 12 $  

 $= 6\,\,circles\,\, $

Hence, we have to shade any \[6\]circles in the box.

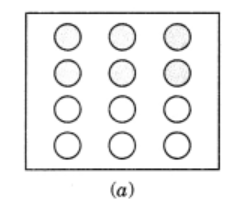
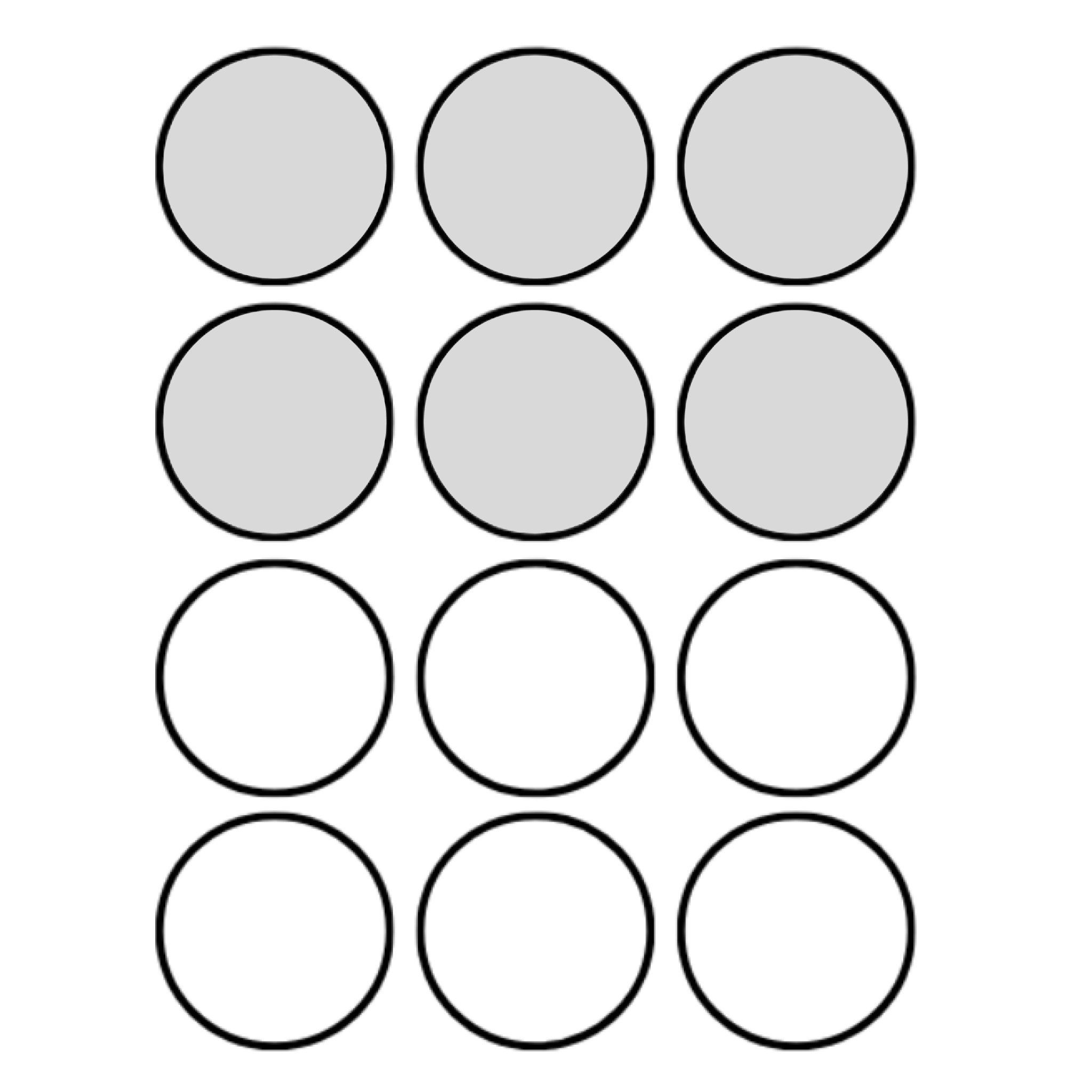
(ii) Given: \[9\] triangles in the box.

We need to shade $\dfrac{2}{3}\,$ of the triangles in the box.

As we know ,there are \[9\] triangles in the box.

$ \Rightarrow \dfrac{2}{3}\,\,of\,the\,\,9\,\,triangles   $

$ = \dfrac{2}{3} \times 9 $

$ = 6\,\,triangles   $

Hence, we have to shade any \[6\,\]triangles in the box.

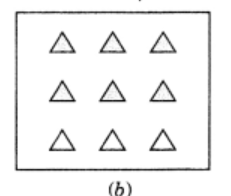
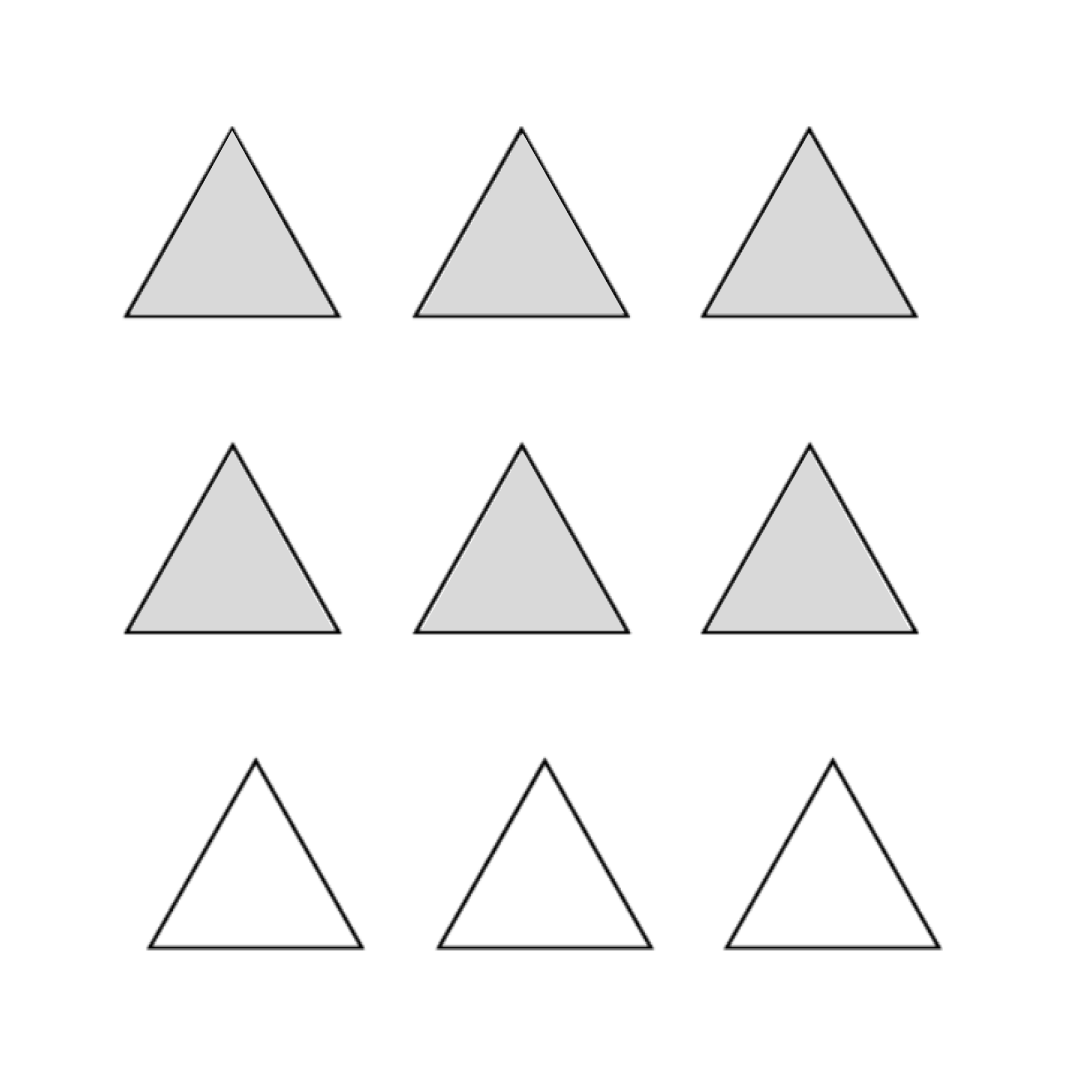
(iii) Given: \[15\] squares in the box.

We need to shade $\dfrac{3}{5}$ of the squares in the box.

As we know ,there are \[15\] squares in the box.

$ \Rightarrow \dfrac{3}{5}\,of\,the\,15\,\,squares   $

  $ = \dfrac{3}{5} \times 15   $ 

   $= \dfrac{3 \times 15}{5} $   

  $ = 3 \times 3   $

  $ = 9\,squares$

Hence, we have to shade any \[9\,\] squares in the box.

5. Find:

(a) $\dfrac{1}{2}\,\,$of (i) \[24\] (ii) \[46\]

Ans:

 (i) \[24\]

We need to find $\dfrac{1}{2}\,$of  \[24\].

Multiplying $\dfrac{1}{2}\,$by \[24\],we get 

$= \dfrac{1}{2} \times 24   $

 $ = 12$

(ii) \[46\]

We need to find $\dfrac{1}{2}\,\,$ of  \[46\].

Multiplying $\dfrac{1}{2}\,$ by \[46\],we get 

$   = \dfrac{1}{2} \times 46   $

$   = 23 $

(b) $\dfrac{2}{3}$ of  (i) \[18\] (ii) \[27\]

Ans: (i) \[18\]

We need to find $\dfrac{2}{3}$ of  \[18\].

Multiplying  $\dfrac{2}{3}$by \[18\],we get 

$ = \dfrac{2}{3} \times 18  $ 

$ = 2 \times 6   $

  $ = 12 $

(ii) \[27\]

We need to find $\dfrac{2}{3}$of  \[27\].

Multiplying $\dfrac{2}{3}$ by \[18\],we get 

$  = \dfrac{2}{3} \times 27   $

$  = 2 \times 9   $

$   = 18 $

(c)  $\dfrac{3}{4}$ of (i) \[16\] (ii) \[36\]

Ans: 

(i) \[16\]

We need to find $\dfrac{3}{4}$ of  \[16\].

Multiplying $\dfrac{3}{4}$ by \[16\],we get 

$= \dfrac{3}{4} \times 16   $

$ = 3 \times 4 $ 

$  = 12  $ 

(ii) \[36\] We need to find  $\dfrac{3}{4}$ of  \[36\].

Multiplying $\dfrac{3}{4}$by \[36\],we get 

$= \dfrac{3}{4} \times 36 $  

$= 3 \times 9   $

$  = 27$

(d) $\dfrac{4}{5}$ of (i) \[20\] (ii) \[35\]

Ans: 

(i) \[20\]

We need to find  $\dfrac{4}{5}$ of  \[20\].

Multiplying $\dfrac{4}{5}$ by \[20\],we get 

$= \dfrac{4}{5} \times 20$   

 $= 4 \times 4   $

 $= 16 $

(ii) \[35\]

We need to find $\dfrac{4}{5}$ of  \[35\].

Multiplying $\dfrac{4}{5}$ by \[35\],we get 

$ = \dfrac{4}{5} \times 35 $

$ = 4 \times 7 $  

$= 28$

6. Multiply and express as a mixed fraction:

(a) \[3 \times 5\dfrac{1}{5}\]

Firstly we need to convert the given mixed fraction into improper fraction.

We take \[5\dfrac{1}{5}\] and multiply \[5\] by \[5\] and add \[1\],we get 

\[ = (5 \times 5) + 1 = 26\]

Using \[26\] as numerator ,we get 

\[5\dfrac{1}{5} = \dfrac{{26}}{5}\]

Now , \[3 \times 5\dfrac{1}{5}\]\[ = 3 \times \dfrac{{26}}{5}\]

$ = \dfrac{3 \times 26}{5}   $

$ = \dfrac{78}{5}   $ 

And  convert it into mixed fraction ,firstly  divide \[78\] by \[5\] and take remainder\[(3)\]as numerator and quotient\[(15)\] as whole number,we get

\[ = 15\dfrac{3}{5}\]

(b) \[5 \times 6\dfrac{3}{4}\]

Firstly we need to convert the given mixed fraction into improper fraction.

We take \[6\dfrac{3}{4}\] and multiply \[6\] by \[4\] and add \[3\],we get 

\[ = (6 \times 4) + 3 = 27\]

Using \[27\] as numerator ,we get 

\[6\dfrac{3}{4} = \dfrac{27}{4}\]

Now , \[5 \times 6\dfrac{3}{4} = 5 \times \dfrac{27}{4}\]

$= \dfrac{5 \times 27}{4} $  

$  = \dfrac{135}{4}$

And convert it into mixed fraction ,firstly  divide \[135\] by \[4\] and take remainder\[(3)\]as numerator and quotient \[(33)\] as whole number,we get

\[ = 33\dfrac{3}{4}\]

(c) \[7 \times 2\dfrac{1}{4}\]

Firstly we need to convert the given mixed fraction into improper fraction.

We take \[2\dfrac{1}{4}\] and multiply \[2\] by \[4\]and add \[1\],we get 

\[ = (2 \times 4) + 1 = 9\]

Using \[9\]as numerator ,we get 

\[2\dfrac{1}{4} = \dfrac{9}{4}\]

Now , \[7 \times 2\dfrac{1}{4} = 7 \times \dfrac{9}{4}\]

\[ = \dfrac{{63}}{4}\] 

And  convert it into mixed fraction ,firstly  divide \[63\] by \[4\] and take remainder\[(3)\]as numerator and quotient \[(15)\] as whole number,we get

\[ = 15\dfrac{3}{4}\]

(d) \[4 \times 6\dfrac{1}{3}\]

 Firstly we need to convert the given mixed fraction into improper fraction.

We take \[6\dfrac{1}{3}\] and multiply \[6\] by \[3\]and add \[1\],we get 

\[ = (6 \times 3) + 1 = 19\]

Using \[19\] as numerator ,we get 

\[6\dfrac{1}{3} = \dfrac{{19}}{3}\]

Now , \[4 \times 6\dfrac{1}{3} = 4 \times \dfrac{{19}}{3}\]

$ = \dfrac{4 \times 19}{3} $  

$= \dfrac{76}{3}    $

And  convert it into mixed fraction ,firstly  divide \[76\] by \[3\] and take remainder \[(1)\]as numerator and quotient \[(25)\] as whole number,we get

\[ = 25\dfrac{1}{3}\]

(e) \[3\dfrac{1}{4} \times 6\]

Firstly we need to convert the given mixed fraction into improper fraction.

We take \[3\dfrac{1}{4}\] and multiply \[3\] by \[4\]and add \[1\],we get 

\[ = (3 \times 4) + 1 = 13\]

Using \[13\] as numerator ,we get 

\[3\dfrac{1}{4} = \dfrac{{13}}{4}\]

Now , \[3\dfrac{1}{4} \times 6 = \dfrac{{13}}{4} \times 6\]

$ = \dfrac{13 \times 3}{2}   $

$ = \dfrac{39}{2} $  

And  convert it into mixed fraction ,firstly  divide \[39\] by \[2\] and take remainder \[(1)\]as numerator and quotient \[(19)\] as whole number,we get

\[ = 19\dfrac{1}{2}\]

(f) \[3\dfrac{2}{5} \times 8\]

Firstly we need to convert the given mixed fraction into improper fraction.

We take \[3\dfrac{2}{5}\] and multiply \[3\] by \[5\]and add \[2\],we get 

\[ = (3 \times 5) + 2 = 17\]

Using \[17\] as numerator ,we get 

\[3\dfrac{2}{5} = \dfrac{{17}}{5}\]

Now , \[3\dfrac{2}{5} \times 8 = \dfrac{{17}}{5} \times 8\]

$ = \dfrac{17 \times 8}{5}  $ 

 $= \dfrac{136}{5} $ 

And convert it into mixed fraction ,firstly  divide \[27\] by \[5\] and take remainder \[(1)\]as numerator and quotient \[(27)\] as whole number,we get

\[ = 27\dfrac{1}{5}\]

7. Find:

(a) $\dfrac{1}{2}$ of  (i) \[2\dfrac{3}{4}\] (ii) \[4\dfrac{2}{9}\]

Ans:

(i) \[2\dfrac{3}{4}\]

We need to find $\dfrac{1}{2}$ of  \[2\dfrac{3}{4}\].

Firstly we need to convert the given mixed fraction into improper fraction.

We take \[2\dfrac{3}{4}\] and multiply \[2\] by \[4\]and add \[3\],we get 

\[ = (2 \times 4) + 3 = 11\]

Using \[11\] as numerator ,we get 

\[2\dfrac{3}{4} = \dfrac{{11}}{4}\]

Now, $\dfrac{1}{2} \times 2\dfrac{3}{4} = \dfrac{1}{2} \times \dfrac{{11}}{4}$

Using Multiplication of Fraction rule ,which  is given by

Product of fraction \[ = \](product of numerator)/(product of denominator) ,we get 

\[ = \dfrac{{11}}{8}\] 

And convert it into mixed fraction ,firstly  divide \[11\] by \[8\] and take remainder \[(3)\] as numerator and quotient \[(1)\] as whole number,we get

\[ = 1\dfrac{3}{8}\]

(ii) \[4\dfrac{2}{9}\]

We need to find $\dfrac{1}{2}$ of  \[4\dfrac{2}{9}\].

Firstly we need to convert the given mixed fraction into improper fraction.

We take \[4\dfrac{2}{9}\] and multiply \[4\] by \[9\] and add \[2\],we get 

\[ = (4 \times 9) + 2 = 38\]

Using \[38\] as numerator ,we get 

\[4\dfrac{2}{9} = \dfrac{{38}}{9}\]

Now, $\dfrac{1}{2} \times 4\dfrac{2}{9} = \dfrac{1}{2} \times \dfrac{38}{9}$

Using Multiplication of Fraction rule which  is given by

Product of fraction \[ = \](product of numerator)/(product of denominator),we get 

\[ = \dfrac{{19}}{9}\] 

And convert it into mixed fraction ,firstly  divide \[19\] by \[9\] and take remainder \[(1)\] as numerator and quotient \[(2)\] as whole number,we get

\[ = 2\dfrac{1}{9}\]

(b) $\dfrac{5}{8}$ of (i) \[3\dfrac{5}{6}\]  (ii) \[9\dfrac{2}{3}\]

Ans:

(i) \[3\dfrac{5}{6}\]

We need to find $\dfrac{5}{8}$ of  \[3\dfrac{5}{6}\].

Firstly we need to convert the given mixed fraction into improper fraction.

We take \[3\dfrac{5}{6}\] and multiply \[3\] by \[6\] and add \[5\],we get 

\[ = (3 \times 6) + 5 = 23\]

Using \[23\] as numerator ,we get 

\[3\dfrac{5}{6} = \dfrac{{23}}{6}\]

Now, $\dfrac{5}{8} \times 3\dfrac{5}{6} = \dfrac{5}{8} \times \dfrac{{23}}{6}$

Using Multiplication of Fraction rule which  is given by

Product of fraction \[ = \](product of numerator)/(product of denominator),we get 

\[ = \dfrac{{115}}{{48}}\] 

And convert it into mixed fraction ,firstly  divide \[115\] by \[48\] and take remainder \[(19)\] as numerator and quotient \[(2)\] as whole number,we get

\[ = 2\dfrac{{19}}{{48}}\]

(ii) \[9\dfrac{2}{3}\]

We need to find $\dfrac{5}{8}$ of  \[9\dfrac{2}{3}\].

Firstly we need to convert the given mixed fraction into improper fraction.

We take \[9\dfrac{2}{3}\] and multiply \[9\] by \[3\] and add \[2\],we get 

\[ = (9 \times 3) + 2 = 29\]

Using \[29\] as numerator ,we get 

\[9\dfrac{2}{3} = \dfrac{{29}}{3}\]

Now, $\dfrac{5}{8} \times 9\dfrac{2}{3} = \dfrac{5}{8} \times \dfrac{{29}}{3}$

Using Multiplication of Fraction rule which  is given by

Product of fraction \[ = \](product of numerator)/(product of denominator),we get 

\[ = \dfrac{{145}}{{24}}\] 

And convert it into mixed fraction ,firstly  divide \[145\] by \[24\] and take remainder \[(1)\] as numerator and quotient \[(6)\] as whole number,we get

\[ = 6\dfrac{1}{{24}}\]

8.  Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidya consumed $\dfrac{2}{5}$of the water. Pratap consumed the remaining water.

(i) How much water did Vidya drink?

(ii) What fraction of the total quantity of water did Pratap drink?

Ans:

Given: Total quantity of water in bottle = \[5\] litres

(i) We know, Vidya consumed =  $\dfrac{2}{5}$ of  \[5\] litres

$ \Rightarrow \dfrac{2}{5} \times 5   $

  $ = 2   $ 

Therefore, Vidya drank 2 litres of water from the bottle.

(ii) We know , Pratap consumed the remaining fraction of water .

So, Pratap consumed \[ = (1 - \dfrac{2}{5})\] part of bottle

                                      \[ = \dfrac{{5 - 2}}{3}\]

                                      \[ = \dfrac{3}{5}\] part of bottle

Pratap consumed $\dfrac{3}{5}$ of \[5\] litres water \[ = \dfrac{3}{5} \times 5\]                                           

                                                            \[ = 3\] litres

Therefore, Pratap drank $\dfrac{3}{5}$ part of the total quantity of water.

Conclusion

NCERT Solutions of Class 7th Maths Chapter 2 Exercise 2.1 Fractions and Decimals act as your guide, helping you understand different types of fractions, perform operations on them, and conquer decimals. Mastering these concepts with practice using the solutions strengthens your math foundation and prepares you for future challenges.

NCERT Solution Class 7 Maths Chapter 2 - Fractions and Decimals Other Exercises

CBSE Class 7 Maths Chapter 2 Other Study Materials

Chapter-Specific NCERT Solutions for Class 7 Maths

Given below are the chapter-wise NCERT Solutions for Class 7 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Related Links for NCERT Class 7 Maths

Access these essential links for NCERT Class 7 Maths, offering comprehensive solutions, study guides, and additional resources to help students master language concepts and excel in their exams.