Master Class 9 Lines and Angles Exercise 6.1 Solutions with Clear Step by Step Guidance
NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles
FAQs on NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles
1. What are NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles Exercise 6.1, and how do they help in CBSE exam preparation?
NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles Exercise 6.1 provide stepwise explanations for each textbook problem as per CBSE 2025–26 syllabus. They help students understand core concepts like types of angles, properties of lines, and reasoning for angle calculation, which improves accuracy in board exams.
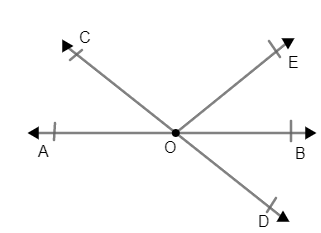
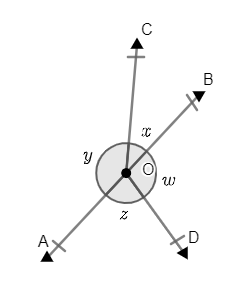
2. How should you solve stepwise problems involving vertically opposite angles in Class 9 Maths Chapter 6?
Begin by identifying intersecting lines and the pairs of vertically opposite angles. Use the property that vertically opposite angles are always equal, write equations for all angles, and solve for unknowns using algebraic steps as given in the NCERT Solutions.
3. What are the key points to remember from NCERT Solutions of Chapter 6 Lines and Angles in Class 9 Maths?
- A line segment joins two endpoints.
- Intersecting lines cut at one point; parallel lines never meet.
- Vertically opposite angles are equal.
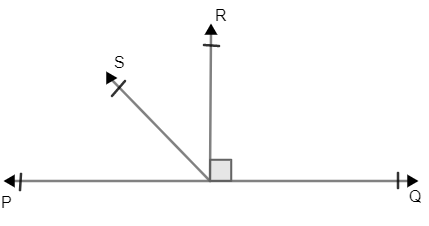
- Complementary angles sum to 90°, supplementary to 180°.
- Understand each angle type: acute, right, obtuse, straight, and reflex.
4. Why is understanding pairs of angles important for solving NCERT Class 9 Maths Chapter 6 questions?
Pairs of angles—such as linear pairs, supplementary, and complementary angles—form the basis for determining unknown angles when lines intersect. Mastering these concepts allows students to solve geometry questions systematically, as required by CBSE board marking schemes.
5. How can the NCERT Solutions for Class 9 Maths Chapter 6 Exercise 6.1 improve conceptual clarity in geometry?
Stepwise NCERT solutions for Exercise 6.1 enhance conceptual clarity by showing logical progressions, using justified properties, and providing visual explanations. This stepwise clarity is essential for both board exams and competitive entrance preparation.
6. What types of errors should be avoided when solving Lines and Angles NCERT questions?
- Avoid misidentifying the type of angle (e.g., mistaking obtuse for reflex).
- Always check that the sum of angles at a point or on a straight line is correct (e.g., 180° or 360°).
- Carefully distinguish between complementary and supplementary angles.
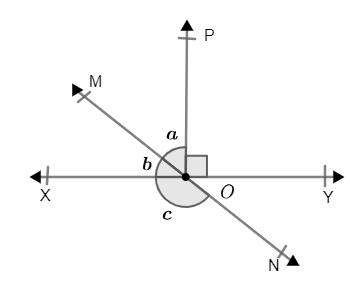
7. In Class 9 Maths Chapter 6, how do you apply the concept of linear pair of angles to prove lines are straight?
For two angles forming a linear pair, their sum is exactly 180°. If you can show that adjacent angles add up to 180° at a given point, you can confirm that the angles are formed on a straight line, using the linear pair axiom taught in NCERT Solutions.
8. What is the significance of Exercise 6.1 in building foundational knowledge for higher-level geometry?
Exercise 6.1 introduces the basic language and properties of lines and angles, which are prerequisites for advanced topics like triangles, quadrilaterals, and theorem proofs in later chapters of the Class 9 Maths NCERT book.
9. Which common misconceptions occur when working with complementary and supplementary angles in Chapter 6?
- Confusing complementary (sum = 90°) and supplementary angles (sum = 180°).
- Assuming all angle pairs formed by intersecting lines are either right or equal, rather than checking the actual measures and definitions.
10. How do the NCERT Solutions for Exercise 6.1 align with the CBSE Class 9 board marking scheme?
Solutions follow the CBSE 2025–26 pattern by providing all steps for full marks, logical reasoning, and correct usage of terminology, ensuring students present their work as expected by examiners in both short and descriptive questions.
11. What steps are recommended if you are unable to solve a sums-based question in Exercise 6.1?
Re-examine the diagram and identify all given and unknown angles, recall properties from the NCERT Solutions (such as those about pairs and types of angles), write stepwise equations for sums, and double-check calculation and logic before finalizing the answer.
12. How does practicing NCERT Solutions for Class 9 Maths Chapter 6 Lines and Angles benefit you in competitive exams beyond board tests?
Mastery of basic geometric concepts and logical reasoning as practiced through NCERT Solutions lays a strong foundation for competitive exams like Olympiads, NTSE, and even JEE/NEET basics, as these exams test core understanding, accuracy, and reasoning skills in mathematics.
13. What are the main learning objectives covered in NCERT Solutions Class 9 Exercise 6.1?
- Correct identification and drawing of line segments, rays, and types of angles.
- Application of vertically opposite, linear pair, and other angle properties to solve problems.
- Development of logical reasoning and proof-writing skills as per CBSE standards.
14. Can different methods be used to solve angle sum problems in Chapter 6 NCERT Solutions?
Yes, some problems may be solved using alternate properties or methods, such as direct calculation, algebraic substitution, or geometric properties, as shown by alternate solutions in the NCERT Solutions for Class 9 Maths Chapter 6.
15. Why is it important to thoroughly practice all questions in NCERT Maths Class 9 Chapter 6 Lines and Angles?
Practicing all NCERT Solutions ensures you cover every question pattern likely to appear in the CBSE 2025–26 exam, develop speed and accuracy, and minimize conceptual errors, leading to strong foundational skills for higher mathematics.




















 Watch Video
Watch Video