NCERT Solutions for Class 9 Maths In Hindi Chapter 8 Quadrilaterals

प्रशावली 8.1

1. एक चतुर्भुज के कोण \[\mathbf{3}\text{ }:\text{ }\mathbf{5}:\text{ }\mathbf{9}\text{ }:\text{ }\mathbf{13}\]के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।

उत्तर: हम जानते हैं कि चतुर्भुज के कोणों का योग \[=360{}^\circ \]

इसलिए, \[3x+5x+9x+13x=360{}^\circ \]

या, \[30x=360{}^\circ \]

या\[,~x=12{}^\circ \]

इसलिए, \[3x=36{}^\circ ,~5x=60{}^\circ ,~9x=108{}^\circ \] और \[13x=156{}^\circ \]

2. यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।

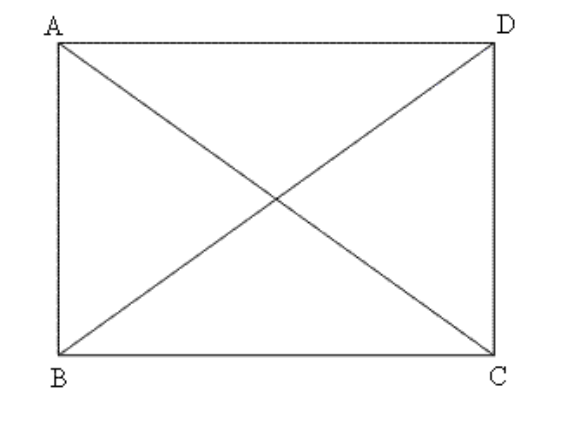
उत्तर: इस समांतर चतुर्भुज के दोनों विकर्ण बराबर हैं।

इसलिए, \[\Delta ABC\cong \Delta ADC\cong \Delta ABD\cong \Delta BCD\]

इसलिए, \[\angle A=\angle B=\angle C=\angle D=90{}^\circ \]

यहाँ पर चारों कोण समकोण हैं, इसलिए दिया गया समांतर चतुर्भुज एक आयत है।

3. दर्शाइए कि यदि के चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।

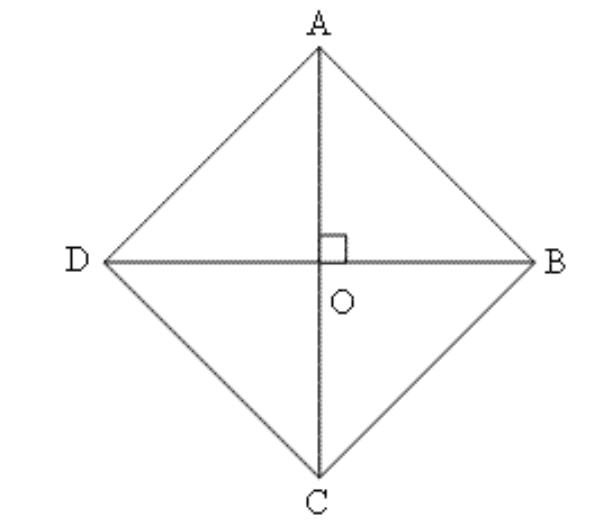
उत्तर: चतुर्भुज \[ABCD\] में विकर्ण \[AC\] और \[BD\] एक दूसरे को समकोण पर समद्विभाजित करते हैं। सिद्ध करना है \[AB\text{ }=\text{ }BC\text{ }=\text{ }CD\text{ }=\text{ }AD\]

\[\Delta AOB\] और \[\Delta AOD\] में

\[DO\text{ }=\text{ }OB\] (\[O\]मध्य बिंदु है)

\[AO\text{ }=\text{ }AO\] (साझा भुजा)

\[\angle AOB\text{ }=\angle AOD\] (समकोण)

इसलिए, \[\Delta AOB\cong \Delta AOD\]

इसलिए, \[AB\text{ }=\text{ }AD\]

इसी तरह \[AB\text{ }=\text{ }BC\text{ }=\text{ }CD\text{ }=\text{ }AD\] भी सिद्ध किया जा सकता है, जिसका मतलब है कि \[ABCD\] एक समचतुर्भुज है।

4. दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।

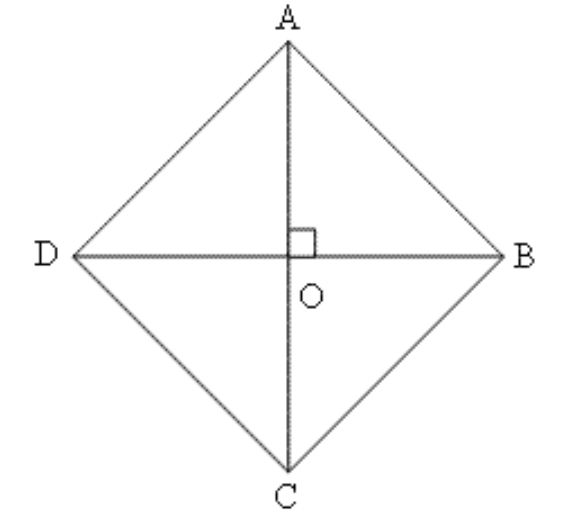
उत्तर: दी गई आकृति में मान लीजिए \[\angle DAB\text{ }=\text{ }90{}^\circ \]

इसलिए, \[\angle DAO\text{ }=\angle BAO\text{ }=\text{ }45{}^\circ \]

इसलिए, \[\angle AOD\text{ }=\text{ }90{}^\circ \]

\[DO\text{ }=\text{ }AO\] (समान कोणों की सामने की भुजाएँ)

इसी तरह \[AO\text{ }=\text{ }OB\text{ }=\text{ }OC\] भी सिद्ध किया जा सकता है। इससे सिद्ध होता है कि वर्ग के विकर्ण बराबर होते हैं।

5. दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर समद्विभाजित करें, तो वह एक वर्ग होता है।

उत्तर: इस प्रश्न के लिए पिछ्ले प्रश्न वाली फिगर का इस्तेमाल करते हैं।

यदि \[DO\text{ }=\text{ }AO\]

तो \[\angle DAO\text{ }=\angle BAO\text{ }=\text{ }45{}^\circ \]

(बराबर भुजाओं के सामने के कोण बराबर होते हैं)

इससे पता चलता है कि चारों कोण समकोण हैं। इसलिए यह एक वर्ग है।

6. एक समांतर चतुर्भुज \[\mathbf{ABCD}\] का विकर्ण \[\mathbf{AC}\] कोण \[\mathbf{A}\] को समद्विभाजित करता है।दर्शाइए कि

1. यह \[\angle C\] को भी समद्विभाजित करता है।

2. \[ABCD\] एक समचतुर्भुज है।

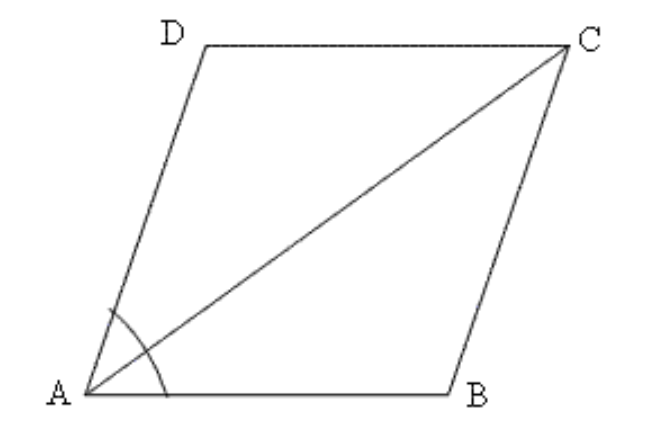
उत्तर\[:~\Delta ADC\] और \[\Delta CBA\] में

\[\angle DAC\text{ }=\angle BCA\] (एकांतर कोण)

\[\angle DCA\text{ }=\angle BAC\] (एकांतर कोण)

\[\angle DAC\text{ }=\angle BAC\] (दिया गया है)

इसलिए, \[\angle DCA\text{ }=\angle DAC\]

इसलिए, \[DA\text{ }=\text{ }DC\]

इसलिए, \[ABCD\] समचतुर्भुज सिद्ध हुआ

7. ABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC कोणों \[\mathbf{A}\] और C दोनों को समद्विभाजित करता है तथा विकर्ण \[\mathbf{BD}\] कोणों \[\mathbf{B}\] और \[\mathbf{D}\] दोनों को समद्विभाजित करता है।

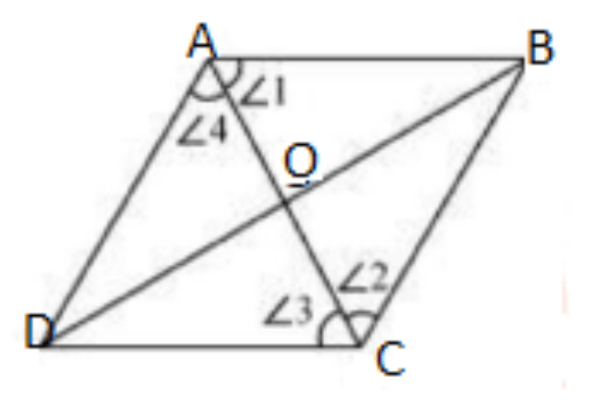
उत्तर: ABCDएक समचतुर्भुज है

 \[\Delta AOD\] में और \[\Delta AOB\]

\[AO\text{ }=\text{ }AO\] (साझा भुजा)

\[AD\text{ }=\text{ }AB\] (समचतुर्भुज की भुजाएँ बराबर होती हैं)

\[DO\text{ }=\text{ }OB\] (समतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।)

इसलिए, \[\Delta AOD\cong \Delta AOB\]

इसलिए, \[\angle DAO\text{ }=\angle BAO\]

इसी तरह निम्नलिखित को सिद्ध किया जा सकता है:

$\angle DCO = \angle BCO$

$\angle ADO =\angle CDO $

$ \angle ABO =\angle CBO $

8. ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि

1. \[\mathbf{ABCD}\] एक वर्ग है

2. विकर्ण \[\mathbf{BD}\] दोनों कोणों \[\mathbf{B}\] और \[\mathbf{D}\] को समद्विभाजित करता है।

उत्तर: \[ABCD\] एक समांतर चतुर्भुज है जिसमें विकर्ण \[AC\] कोण \[\angle DAB\] को समद्विभाजित करता है।

\[\Delta ADC\] और \[\Delta ABC\] में

\[\angle DAC\text{ }=\angle BAC\] (विकर्ण इन कोणों को समद्विभाजित कर रहा है)

\[AC\text{ }=\text{ }AC\] (साझा भुजा)

\[AD\text{ }=\text{ }BC\] (समांतर चतुर्भुज की समांतर भुजाएँ आपस में बराबर होती हैं)

इसलिए, \[\Delta ADC\cong \Delta ABC\]

इसलिए, \[\angle DCA\text{ }=\angle BCA\]

इससे सिद्ध होता है कि \[AC\] कोण \[\angle DCB\] को भी समद्विभाजित करता है।

अब मान लीजिए कि एक अन्य विकर्ण \[DB\] विकर्ण \[AC\] को \[O\] पर काटता है।

चूँकि यह एक समांतर चतुर्भुज है इसलिए विकर्ण \[DB\] और \[AC\] परस्पर समद्विभाजक हैं।

\[\Delta AOD\] और \[\Delta BOD\] में

\[\angle DAO\text{ }=\angle DCO\] 

(समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं इसलिए उनके आधे भी बराबर होंगे।)

\[AO\text{ }=\text{ }CO\] और \[DO\text{ }=\text{ }DO\]

इसलिए \[\Delta AOD\cong \Delta BOD\]

इसलिए, \[\angle DOA\text{ }=\angle DOB=90{}^\circ \]

चूँकि विकर्ण एक दूसरे पर लम्ब हैं इसलिए यह एक समचतुर्भुज है।

9. समांतर चतुर्भुज \[\mathbf{ABCD}\] के विकर्ण \[\mathbf{ED}\] पर दो बिंदु \[\mathbf{P}\] और \[\mathbf{Q}\] इस प्रकार स्थित हैं कि \[\mathbf{DP}\text{ }=\text{ }\mathbf{BQ}\] है।दर्शाइए कि

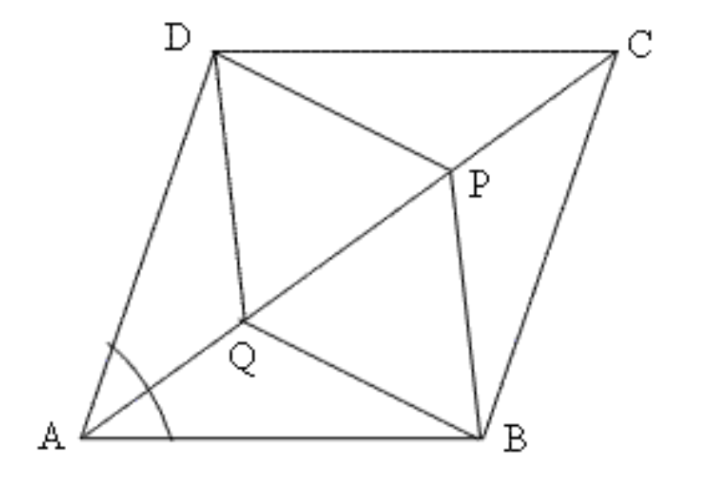
 $i)\mathbf{\Delta APD}\cong \mathbf{\Delta CQB}$

 $ii)\mathbf{AP}\text{ }=\text{ }\mathbf{CQ}$

 $iii)\mathbf{\Delta AQB}\cong \mathbf{\Delta CPD}$

 $iv)\mathbf{AQ}\text{ }=\text{ }\mathbf{CP} $

\[APCQ\] एक समांतर चतुर्भुज है।

उत्तर: \[\Delta APD\] और \[\Delta CQB\] में

\[DP\text{ }=\text{ }BQ\] (दिया गया है)

\[AD\text{ }=\text{ }BC\] (सम्मुख भुजाएँ)

\[\angle DAP\text{ }=\angle BCQ\] (सम्मुख कोण के आधे भी बराबर होंगे।)

इसलिए\[,\text{ }\Delta APD\cong \Delta CQB\]

इसलिए, \[AP\text{ }=\text{ }CQ\] सिद्ध हुआ

अब\[,\text{ }\Delta AQB\] और \[\Delta CPD\] में

\[AB\text{ }=\text{ }CD\] (समुख भुजाएँ)

\[DP\text{ }=\text{ }BQ\] (दिया गया है)

\[\angle BAQ\text{ }=\angle DCP\] (सम्मुख कोण के आधे भी बराबर होंगे।)

इसलिए, \[\Delta AQB\cong \Delta CPD\]

इसलिए, \[AQ\text{ }=\text{ }CP\] सिद्ध हुआ

इसलिए\[\angle DPA\text{ }=\angle BQP\] 

(सर्वांगसम त्रिभुज \[APD\] और \[CQB\] के संगत कोण)

\[\Delta DQP\] और \[\Delta BQP\] में

\[\angle DPQ\text{ }=\angle BQP\] (पिछले प्रमाण से)

\[DP\text{ }=\text{ }BQ\] (दिया गया है)

\[PQ\text{ }=\text{ }PQ\] (साझा भुजा)

इसलिए\[,\text{ }\Delta DQP\cong \Delta BQP\]

इसलिए, \[\angle QDP\text{ }=\angle QBP\]

बराबर सम्मुख भुजाओं और बराबर सम्मुख कोणों से यह सिद्ध होता है कि \[APCQ\] एक समांतर चतुर्भुज है।

10. ABCD एक समांतर चतुर्भुज है तथा \[\mathbf{AP}\] और \[\mathbf{CQ}\] शीर्षों \[\mathbf{A}\] और \[\mathbf{C}\] से विकर्ण \[\mathbf{BD}\] पर क्रमश: लम्ब हैं। दर्शाइए कि

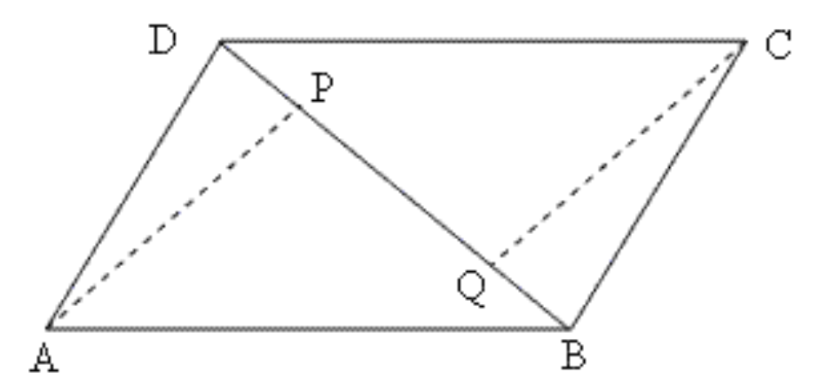
$   i)\Delta APB\cong \Delta CQD $

$   ii)AP\text{ }=\text{ }CQ $

उत्तर\[:~\Delta APB\] और \[\Delta CQD\] में

\[\angle ABP\text{ }=\angle CDQ\] (एकांतर कोण)

\[AB\text{ }=\text{ }CD\]

\[\angle APB\text{ }=\angle CQD\] (समकोण)

इसलिए, \[\Delta APB\cong \Delta CQD\]

इसलिए, \[AP\text{ }=\text{ }CQ\]

11. \[\mathbf{\Delta }\text{ }\mathbf{ABC}\] और \[\mathbf{\Delta DEF}\] में, \[\mathbf{AB}\text{ }=\text{ }\mathbf{DE},\text{ }\mathbf{AB}\text{ }||\text{ }\mathbf{DE},\text{ }\mathbf{BC}\text{ }=\text{ }\mathbf{EF}\] और \[\mathbf{BC}\text{ }||\text{ }\mathbf{EF}\] है। शीर्षों \[\mathbf{A},\text{ }\mathbf{B}\] और \[\mathbf{C}\] को क्रमश: शीर्षों \[\mathbf{D},\text{ }\mathbf{E}\], और \[\mathbf{F}\] से जोड़ा जाता है। दर्शाइए कि

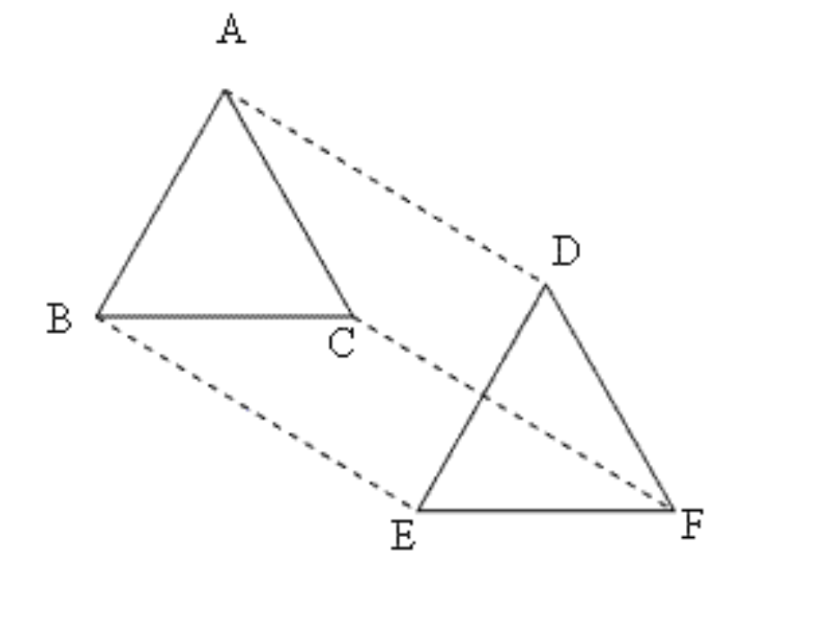
1. चतुर्भुज \[\mathbf{ABED}\] एक समांतर चतुर्भुज है।

2. चतुर्भुज \[\mathbf{BEFC}\] एक समांतर चतुर्भुज है।

3. \[\mathbf{AD}\text{ }||\text{ }\mathbf{CF}\] और \[\mathbf{AD}\text{ }=\text{ }\mathbf{CF}\] है।

4. \[\mathbf{AC}\text{ }=\text{ }\mathbf{DF}\] है।

5. \[\mathbf{\Delta ABC}\cong \mathbf{\Delta DEF}\] है।

उत्तर: \[\Delta ABC\] और \[\Delta DEF\] में

\[AB\text{ }=\text{ }DE\] (दिया गया है)

\[BC\text{ }=\text{ }EF\] (दिया गया है)

\[\angle \] \[ABC\text{ }=\angle DEF\] (\[AB||DE\] और \[BC||EF\] हैं)

इसलिए, \[\Delta ABC\cong \Delta DEF\]

चतुर्भुज \[ABED\] में

$ AB = ED $

AB||ED 

इसलिए, \[ABED\] एक समांतर चतुर्भुज है (सम्मुख भुजाएँ समांतर और बराबर हैं)

इसलिए, \[BE||AD\text{ }...............\left( 1 \right)\]

इसी तरह ACFD समांतर चतुर्भुज सिद्ध किया जा सकता है।

इसलिए\[,\text{ }BE||CF\text{ }.............\text{ }\left( 2 \right)\]

समीकरण \[(1)\]और \[(2)\]से यह सिद्ध होता है कि:

\[AD||CF\]

इसलिए\[,\text{ }AD\text{ }=\text{ }CF\]

इसी तरह हम सिद्ध कर सकते हैं:

\[AC\text{ }=\text{ }DF\] और \[AC||DF\]

12. ABCD एक समलंब है, जिसमें \[AB\text{ }||\text{ }DC\] और \[AD\text{ }=\text{ }BC\] है। दर्शाइए कि

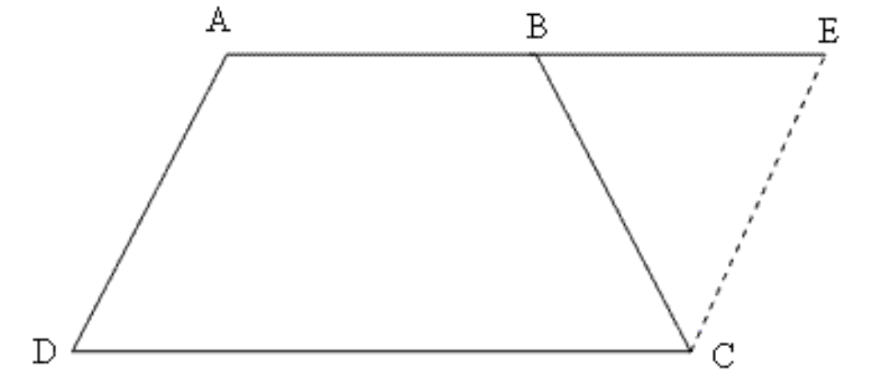
1. $\angle A=\angle B  $

2. $\angle C=\angle D  $

3. \[\Delta ABC\cong \Delta BAD\]

4. विकर्ण  AC  विकर्ण  BD है।

उत्तर: \[\Delta BCE\] में

\[EC\text{ }=\text{ }AD\] (समांतर चतुर्भुज की सम्मुख भुजाएँ)

\[AD\text{ }=\text{ }BC\] (दिया गया है)

इसलिए\[,\text{ }BC\text{ }=\text{ }EC\]

इसलिए, \[\angle CBE\text{ }=\angle CEB\]

\[\angle CBE\text{ }+\angle CBA\text{ }=\text{ }180{}^\circ \] (कोणों का रैखिक युग्म)

\[\angle CEB\text{ }+\angle DAB\text{ }=\text{ }180{}^\circ \] (समांतर चतुर्भुज के आसन्न कोण)

\[\angle CBE\text{ }=\angle CEB\] रखने पर यह स्पष्ट हो जाता है

\[\angle DBA\text{ }=\angle CBA\]

अब, \[\angle DAB\text{ }+\angle CDA\text{ }=\text{ }180{}^\circ \] (आसन्न कोण)

और, \[\angle CBA\text{ }+\angle DCB\text{ }=\text{ }180{}^\circ \] (आसन्न कोण)

चूँकि \[\angle DBA\text{ }=\angle CBA\] इसलिए यह स्पष्ट है \[\angle CDA\text{ }=\angle DCB\]

\[\Delta ABC\] और \[\Delta BAD\] में

\[AB\text{ }=\text{ }AB\] (साझा भुजा)

\[AD\text{ }=\text{ }BC\] (दिया गया है)

\[\angle DBA\text{ }=\angle CBA\]

इसलिए\[,\text{ }\Delta ABC\cong \Delta BAD\]

प्रश्नावली 8.2

1. \[\mathbf{ABCD}\] एक चतुर्भुज है जिसमें \[\mathbf{P},\text{ }\mathbf{Q},\text{ }\mathbf{R}\] और \[\mathbf{S}\] क्रमश: भुजाओं \[\mathbf{AB},\text{ }\mathbf{BC},\text{ }\mathbf{CD}\] और \[\mathbf{DA}\] के मध्य बिंदु हैं। \[\mathbf{AC}\] उसका एक विकर्ण है। दर्शाइए कि

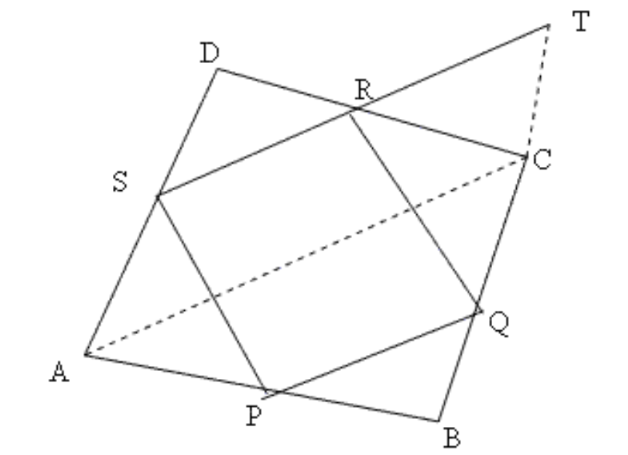
1. \[\mathbf{SR}\text{ }||\text{ }\mathbf{AC}\] और \[\mathbf{SR}\text{ }=~\frac{\mathbf{1}}{\mathbf{2}}~\mathbf{AC}\] है।

2. \[\mathbf{PQ}\text{ }=\text{ }\mathbf{SR}\] है।

3. \[\mathbf{PQRS}\] एक समांतर चतुर्भुज है।

उत्तर: भुजा \[SR\] को \[T\] तक बढ़ाईए ताकि \[CT\] और \[AS\] समांतर हो जाएँ

\[\Delta DSR\] और \[\Delta CRT\] में

\[DR\text{ }=\text{ }RC\] (\[R\] भुजा \[DC\] का मध्यबिंदु है)

\[\angle DRS\text{ }=\angle TRS\] (सम्मुख कोण)

\[\angle DSR\text{ }=\angle RTC\] (\[ST\] के एकांतर कोण)

इसलिए, \[\Delta DSR\cong \Delta CRT\]

इसलिए\[,\text{ }SR\text{ }=\text{ }RT\]

\[ST\text{ }=\text{ }AC\] (सम्मुख भुजाएँ)

इसलिए\[,~SR=\frac{1}{2}AC\]

चूँकि \[DA\] और \[DC\] के मध्य बिंदुओं को SR स्पर्श करता है, मध्य बिंदु प्रमेय के अनुसार, \[SR||AC\]

इसी तरह \[AC\text{ }||\text{ }PQ\] को सिद्ध किया जा सकता है जिससे यह साबित होगा कि \[PQRS\] एक समांतर चतुर्भुज है।

2. \[\text{ }\mathbf{ABCD}\] एक समचतुर्भुज है, जिसमें \[\mathbf{P},\text{ }\mathbf{Q},\text{ }\mathbf{R}\] और \[\mathbf{S}\] क्रमश: भुजाओं \[\mathbf{AB},\text{ }\mathbf{BC},\] \[\mathbf{CD}\] और \[\mathbf{DA}\] के मध्य बिंदु हैं। दर्शाइए कि \[\mathbf{PQRS}\] एक आयत है।

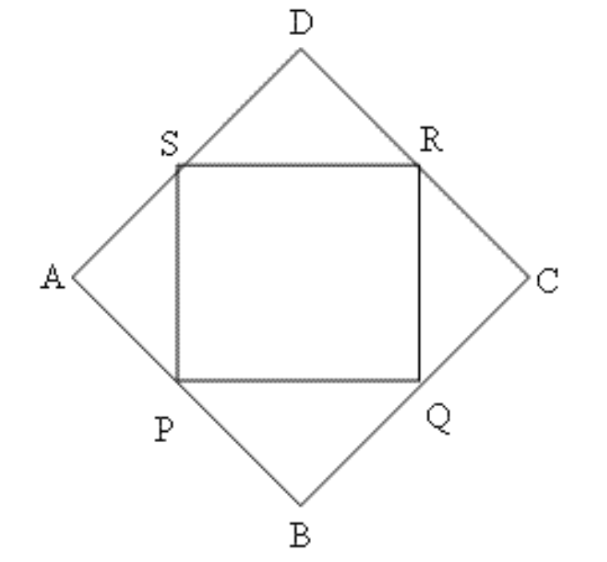
उत्तर: पिछले प्रश्न के हल की तरह हम यह सिद्ध कर सकते हैं कि \[PQRS\] एक समांतर चतुर्भुज है। उसके बाद इसे आयत सिद्ध करने के लिए हमें नीचे दी बात को सिद्ध करना होगा।

\[\angle S\text{ }=\angle R\text{ }=\angle Q\text{ }=\angle P\text{ }=\text{ }90{}^\circ \]

\[\Delta DSR,\text{ }\Delta CRQ,\text{ }\Delta BQP,\Delta APS\] में

\[DS\text{ }=\text{ }CR\text{ }=\text{ }BQ\text{ }=\text{ }AP\text{ }=\text{ }DR\text{ }=\text{ }CQ\text{ }=\text{ }BP\text{ }=\text{ }AS\] 

(समतुर्भुज की भुजाएँ समान होती हैं और \[PQRS\] इन भुजाओं के मध्य बिंदु हैं)

\[\angle DSR\text{ }=\angle DRS\text{ }=\angle CRQ\text{ }=\angle CQR\text{ }=\angle BQP\text{ }=\angle BPQ\text{ }=\angle APS\text{ }=\angle ASP\]

इसलिए, \[\Delta DSR\cong \Delta CRQ\cong \Delta BQP\cong \Delta APS\]

इसलिए, \[\angle SDR\text{ }=\angle CRQ\text{ }=\angle QBP\text{ }=\angle PAS\text{ }=\text{ }90\]

इसलिए, \[\angle DSR\text{ }+\angle DRS\text{ }=\text{ }90{}^\circ \]

या, \[\angle DSR\text{ }=\angle DRS\text{ }=\angle CRQ\text{ }=\angle CQR\text{ }=\angle BQP\text{ }=\angle BPQ\text{ }=\angle APS\text{ }=\angle ASP\]

चूँकि, \[\angle ASP\text{ }+\angle PSR\text{ }+\angle DSR\text{ }=\text{ }180{}^\circ \]

या, \[\angle PSR\text{ }=\text{ }180{}^\circ -\left( 45{}^\circ \text{ }+\text{ }45{}^\circ  \right)\text{ }=\text{ }90{}^\circ \]

इसी तरह, \[\angle S\text{ }=\angle R\text{ }=\angle Q\text{ }=\angle P\text{ }=\text{ }90{}^\circ \]

इसलिए, \[PQRS\] एक आयत है

3. \[\mathbf{ABCD}\] एक आयत है, जिसमें \[\mathbf{P},\text{ }\mathbf{Q},\text{ }\mathbf{R}\] और \[\mathbf{S}\] क्रमश: भुजाओं \[\mathbf{AB},\text{ }\mathbf{BC},\text{ }\mathbf{CD}\] और \[\mathbf{DA}\] के मध्य बिंदु हैं। दर्शाइए कि \[\mathbf{PQRS}\] एक समचतुर्भुज है।

उत्तर: \[\Delta APS\] और \[\Delta BPQ\] में

\[AP\text{ }=\text{ }PB\] (\[AB\] का मध्य बिंदु \[P\] है)

\[AS\text{ }=\text{ }BQ\] (बराबर भुजाओं के आधे भी बराबर होते हैं)

\[\angle PAS\text{ }=\text{ }\angle PBQ\] (समकोण)

इसलिए, \[\Delta APS\cong \Delta BPQ\]

इसलिए, \[PS\text{ }=\text{ }PQ\]

इसी तरह निम्नलिखित को सिद्ध किया जा सकता है:

$SR = QR $ 

$ QR =PQ $

इसलिए, \[PQ\text{ }=\text{ }QR\text{ }=\text{ }RS\text{ }=\text{ }SP\]

इसलिए, \[PQRS\] एक समचतुर्भुज है।

4. \[\mathbf{ABCD}\] एक समलंब है, जिसमें \[\mathbf{AB}\text{ }||\text{ }\mathbf{CD}\] है। साथ ही, \[\mathbf{BD}\] एक विकर्ण है और \[\mathbf{E}\] भुजा \[\mathbf{AD}\] का मध्य बिंदु है। \[\mathbf{E}\] से होकर एक रेखा \[\mathbf{AB}\] के समांतर खींची गई है, जो \[\mathbf{BC}\] को \[\mathbf{F}\] पर प्रतिच्छेद करती है। दर्शाइए कि \[\mathbf{F}\] भुजा \[\mathbf{BC}\] का मध्यु बिंदु है।

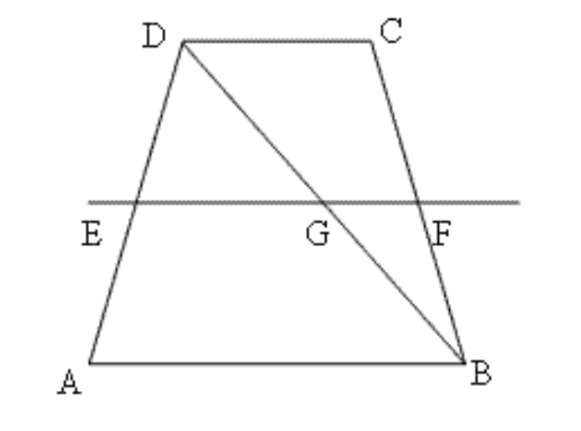
उत्तर: \[\Delta \text{ }ADB\] में,

\[DG\text{ }=\text{ }GB\]

हम जानते हैं कि त्रिभुज के आधार के समांतर और दूसरी भुजा के मध्य बिंदु से निकलने वाली भुजा उस त्रिभुज की तीसरी भुजा को समद्विभाजित करती है।

$AB || DC  $

$AB || EF $

इसलिए, \[EF\text{ }||\text{ }DC\]

इसलिए\[,\text{ }\Delta \text{ }ADB\] में

\[EG\text{ }||\text{ }AB\]

\[E\] भुजा \[AD\] का मध्य बिंदु है।

इसलिए, \[DB\] का मध्य बिंदु \[G\] है।

अब, \[\Delta \text{ }DCB\] में

\[GF\text{ }||\text{ }DC\]

\[BD\] का मध्य बिंदु \[G\] है।

इसलिए, \[BC\] का मध्य बिंदु \[F\] है।( मध्य बिंदु प्रमेय के अनुसार)

5. एक समांतर चतुर्भुज \[\mathbf{ABCD}\] में \[\mathbf{E}\] और \[\mathbf{F}\] क्रमश: भुजाओं \[\mathbf{AB}\] और \[\mathbf{CD}\] के मध्य बिंदु हैं। दर्शाइए कि रेखाखंड \[\mathbf{AF}\] और \[\mathbf{EC}\] विकर्ण \[\mathbf{BD}\] को समत्रिभाजित करते हैं।

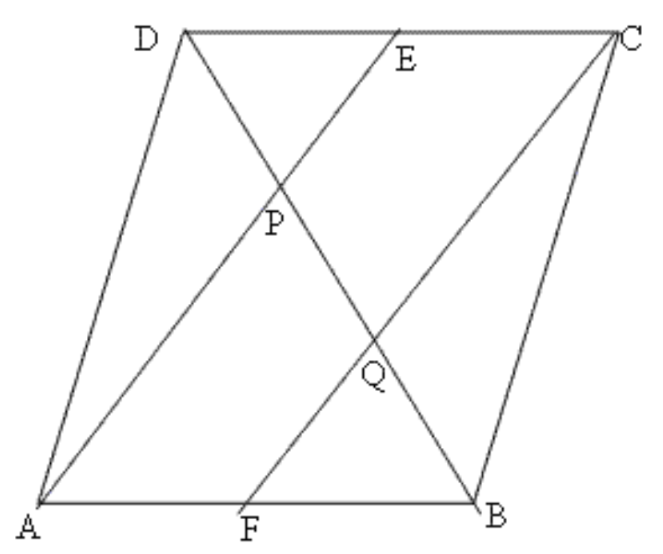
उत्तर: \[\Delta ADE\] और \[\Delta CBF\] में

\[AD\text{ }=\text{ }BC\] (समांतर चतुर्भुज की सम्मुख भुजाएँ)

\[BF\text{ }=\text{ }DE\] (समांतर चतुर्भुज की सम्मुख भुजाओं का आधा)

\[\angle ADE\text{ }=\angle CBF\] (सम्मुख कोण)

इसलिए, \[\Delta ADE\cong \Delta CBF\]

इसलिए, \[AE\text{ }=\text{ }CF\]

चतुर्भुज \[AECF\] में

\[EC\text{ }||\text{ }AF\] और \[EC\text{ }=\text{ }AF\]

\[AE\text{ }=\text{ }CF\]

इसलिए, \[AE\text{ }||\text{ }CF\]

इसलिए, \[AECF\] एक समांतर चतुर्भुज है।

\[\Delta \text{ }DQC\] में

\[PE\text{ }||\text{ }QC\] (\[AE\text{ }||\text{ }CF\] सिद्ध करते हुए पहले सिद्ध किया जा चुका है।)

\[DC\] का मध्य बिंदु \[E\] है।

इसलिए, \[DQ\] का मध्य बिंदु \[P\] है।

इसलिए, \[DP\text{ }=\text{ }PQ\]

\[\Delta \text{ }APB\] में

\[FQ\text{ }||\text{ }AP\]

\[AB\] का मध्य बिंदु \[F\] है।

इसलिए\[,\text{ }PQ\text{ }=\text{ }QB\]

इसलिए, \[DP\text{ }=\text{ }PQ\text{ }=\text{ }QB\] सिद्ध हुआ।

6. दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य बिंदुओं को मिलाने वाले रेखाखंड परस्पर समद्विभाजित करते हैं।

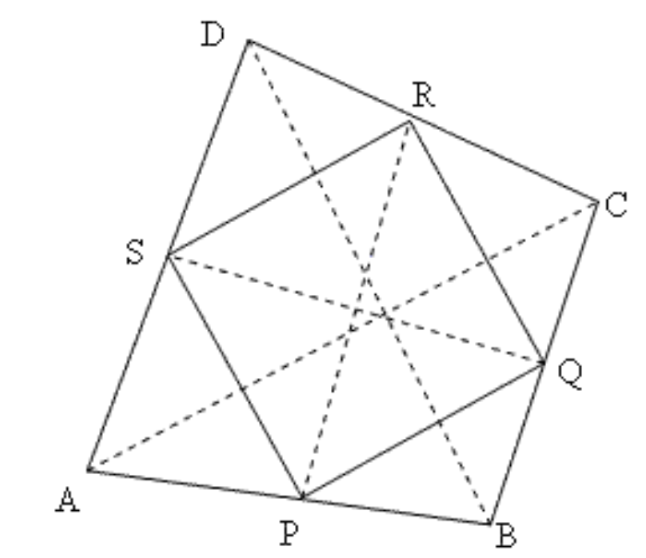
उत्तर: \[ABCD\] एक चतुर्भुज है जिसमें \[AB,\text{ }BC,\text{ }CD\] और \[AD\] के मध्य बिंदु क्रमश: \[P,\] \[Q,\text{ }R,\]और \[S\] हैं।

\[\Delta \text{ }ACD\] में

\[CD\] और \[AD\] के मध्यबिंदुओं को SR स्पर्श करता है।

इसलिए, \[SR\text{ }||\text{ }AC\]

इसी तरह निम्नलिखित को सिद्ध किया जा सकता है।

$ PQ ||AC $

$ QR || BD  $

$PS || BD  $

इसलिए, \[PQRS\] एक समांतर चतुर्भुज है।

\[PR\] और \[QS\] समांतर चतुर्भुज \[PQRS\] विकर्ण हैं, इसलिए दोनों एक दूसरे को समद्विभाजित करते हैं ।

7. \[\text{ }\mathbf{ABC}\] एक त्रिभुज है जिसका कोण \[\mathbf{C}\] समकोण है। कर्ण \[\mathbf{AB}\] के मध्य बिंदु M से होकर \[\mathbf{BC}\] के समांतर खींची गई रेखा \[\mathbf{AC}\] को \[\mathbf{D}\] पर प्रतिच्छेद करती है। दर्शाइए कि

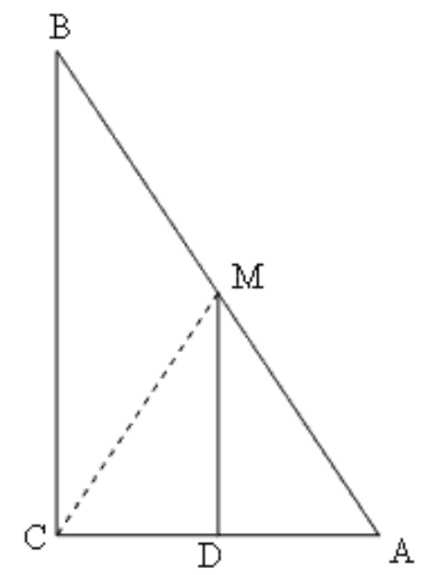
1. \[\mathbf{D}\] भुजा \[\mathbf{AC}\] का मध्य बिंदु है।

2. \[\mathbf{MD}\bot \mathbf{AC}\] है।

3. \[\mathbf{CM}\text{ }=\text{ }\mathbf{MA}\text{ }=~\frac{\mathbf{1}}{\mathbf{2}}~\mathbf{AB}\] है।

उत्तर: \[DM\text{ }||\text{ }BC\]

\[AB\] का मध्य बिंदु \[M\] है।

इसलिए, \[AC\] का मध्य बिंदु \[D\] है।(मध्य बिंदु प्रमेय के अनुसार)

\[\angle ACD\text{ }=\angle MDA\text{ }=\text{ }90{}^\circ \] (तिर्यक रेखा \[MD\] के एकांतर कोण)

अब, \[\Delta CDM\] और \[\Delta ADM\] में

$ CD = AD $

$  MD = MD$

$ \angle MDC =\angle MDA  $

इसलिए\[,\text{ }\Delta CDM\cong \Delta ADM\] (\[SAS\] प्रमेय के अनुसार)

इसलिए, \[MC\text{ }=\text{ }MA\]

\[MA=\frac{1}{2}AB\]

इसलिए, \[MC=MA=\frac{1}{2}AB\]

NCERT Solutions for Class 9 Maths  Chapter 8 Quadrilaterals In Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 9 Maths Chapter 8 solution Hindi medium is created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 9 Maths Chapter 8 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 9 Maths Chapter 8 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 9 Maths Quadrilaterals solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that. 

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 9 Maths Quadrilaterals in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 9 can download these solutions at any time as per their convenience for self-study purpose. 

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 9 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.