




Electric Charges and Fields - An Important Concept of Physics
The chapter Electric Charges and Fields notes down some of the most important concepts of electric charges and fields for NEET, JEE, and other competitive exams. In the Electric Charges and Fields chapter, students will study the basic properties of electric charge, conductors, and insulators, and some laws related to them.
The chapter on Electric Charges and Fields begins with the very basic definition of Coulomb’s law, Electrostatic Forces, Dielectric, Electric Field, and what are different charge distributions helpful in studying the chapter ahead. These concepts will lead us to a very important part of the chapter, i.eVector notations of Electric Field, Electric Lines of Forces, Energy Density, and Electric Dipole.
The concepts mentioned above will help us in studying the chapter deeply along with the hands-on practice of many important numerical problems that will help us in acing the exams.
In this article, we will cover the important concepts and topics with the Electric Charges and Fields formulas as well as Electric Charges and Fields solutions for numericals that will help students to revise and boost their preparations for NEET and JEE.
Important Topics of Thermal Physics
Electric Charges and properties
Coulomb's Law
Electric Field
Conductors and Insulators
Dielectric
Electric Lines of Forces
Electric Flux
Electric Dipole
Gauss's Law
Important Concepts of Thermal Physics
List of Important Formulae of Electric Charges and Fields
Solved Examples of Electric Charges and Fields
1. An electric dipole with a dipole moment $4 \times 10^{-9}$ C/m aligned at $30^{\circ}$ with the direction of a uniform electric field of magnitude $5 \times 10^{4}$N/C. Calculate the magnitude of torque acting on the dipole.
Sol:
Given,
Dipole moment p = $4 \times 10^{-9}$ C/m
E = $5 \times 10^{4}$N/C and angle = $30^{\circ}$
Torque = $\tau= \vec{p}\times \vec{E}$ = pEsin$\theta$
=$4 \times 10^{-9}$ $5 \times 10^{4}$ sin$30^{\circ}$
=$\times 10^{-4}$Nm is the correct answer.
Key point: Here, the formula of torque due to an electric dipole can be used directly.
2.Consider a uniform electric field E = $3 \times 10^{3}\hat{i}$N/C.
(a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane(b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
Sol:
Given,
(a) E = $3 \times 10^{3}\hat{i}$N/C, side of square = 10cm = 0.1m
Area of square = 0.01m2.
Since the plane of square is parallel to the yz plane and the area vector is also in this plane so the angle between E and area vector is zero.
$\phi$= $\vec{E}.\vec{S}$
= $\phi$= $ \phi$= $\vec{E}\vec{S}\cos\theta$
= $3 \times 10^{3} \times 0.01 \cos 0^{\circ}$
=30 Nm2/C.
(b) $\phi$= $\vec{E}.\vec{S}$
= $\phi$= $ \phi$= $\vec{E}\vec{S}\cos\theta$
=$3 \times 10^{3}\times 0.01 \cos 60^{\circ}$
= 15 Nm2/C
Key point: Here, the formula of electric flux can be used directly.
Previous Year Questions of Electric Charges and Fields
1. Two parallel infinite line charges with linear charge densities +$\lambda$ C/m and -$\lambda$ C/m are placed at a distance of 2R in free space. What is an electric charge field midway between the two line charges? (NEET 2019)
Zero
$\dfrac{2 \lambda}{\pi \varepsilon_{\circ}R}$ N/C
$\dfrac{\lambda}{\pi \varepsilon_{\circ}R}$ N/C
$\dfrac{\lambda}{2\pi \varepsilon_{\circ}R}$ N/C
Sol:
Given,
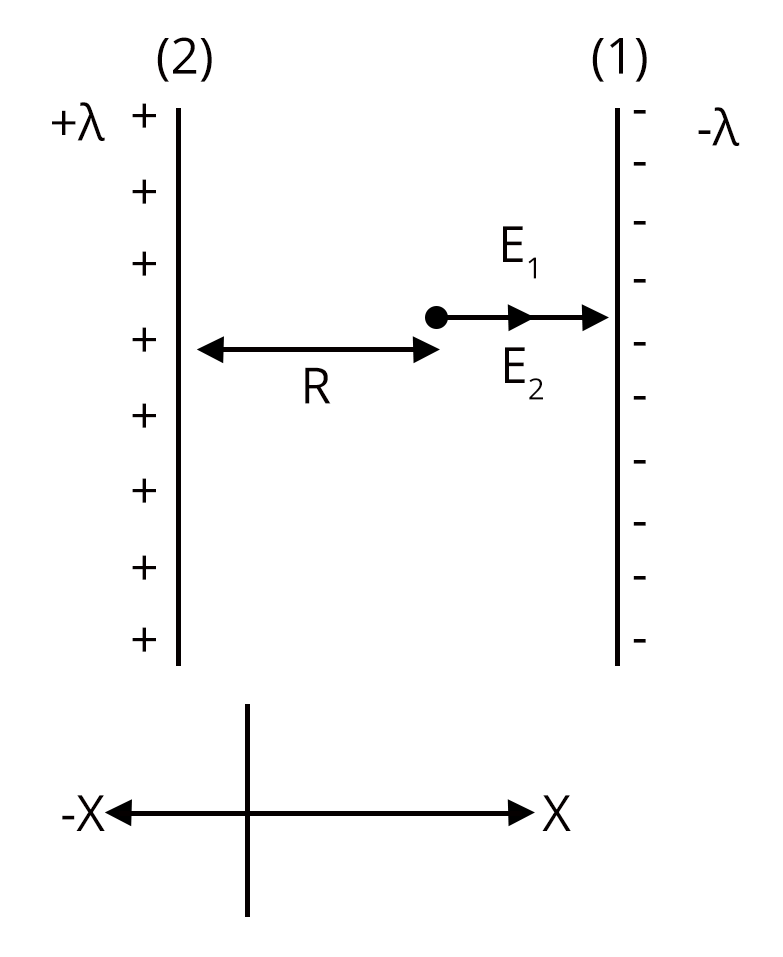
As one can clearly see the linear charge distribution of parallel plates and the direction of $\vec{E}$ by both the plates on each other so the electric field due to plate 1 having linear charge density -$\lambda$ is
$\vec{E_{1}}$ = $\dfrac{\lambda}{2\pi \varepsilon_{\circ}R}\hat{i}$ N/C
Similarly the electric field due to plate 2 having linear charge density +$\lambda$ is
$\vec{E_{2}}$ = $\dfrac{\lambda}{2\pi \varepsilon_{\circ}R}\hat{i}$ N/C
As the Electric Field follows the vector superposition principle so the net $\vec{E}$ = $\vec{E_{1}}$ +$\vec{E_{2}}$
= $\dfrac{\lambda}{2\pi \varepsilon_{\circ}R}\hat{i}$ + $\dfrac{\lambda}{2\pi \varepsilon_{\circ}R}\hat{i}$
=$\dfrac{\lambda}{\pi \varepsilon_{\circ}R}\hat{i}$
Which is option (c)
Trick: The relationship between the Electric Field having $\lambda$ as linear charge density is $\vec{E}$ = $\dfrac{\lambda}{2\pi \varepsilon_{\circ}R}$.
2. Two point charges A and B, having charges Q and -Q respectively, are placed at a certain distance apart and the force acting between them is F. If 25% charge of A is transferred to B, then the force between charges becomes: (NEET 2019)
F
9F/16
16F/9
4F/3
Sol:
Given,

We have been provided two point charges A and B having charges +Q and -Q separated by distance r having force F between them.
Hence F = $\dfrac{KQ^{2}}{r^{2}}$
Now 25% of the charge is transferred from A to B then the charge left on A
$Q_A^\bracevert$ = Q- $\dfrac{Q}{4}$ = $\dfrac{3Q}{4}$
Similarly the charge on B now is
$Q_B^\bracevert$ = - Q+ $\dfrac{Q}{4}$ = $\dfrac{-3Q}{4}$
So the new forces due to $Q_A^\bracevert$ and $Q_B^\bracevert$
$F^{\bracevert}$ = $\dfrac{\dfrac{(3Q)}{4}^{2}}{r^{2}}$
$F^{\bracevert}$ = 9/16 $\dfrac{KQ^{2}}{r^{2}}$
Which is option (b)
Trick: Here, the formula of electrostatic force between two charge particles can be used directly.
Practice Questions
1. A Conducting sphere of radius 10cm has an unknown Charge. If the Electric Field at a Point 20cm from the center of the sphere of magnitude 1.5×103 N/C is directed radially inwards, what is the net charge on the sphere?
(Ans: 6.67nC)
2. Four charges qA = 2 microcoulomb, qB = -5 microcoulomb,qC = 2 microcoulomb,qD = -5 microcoulomb are located at the corners of a square ABCD of side 10cm. What is the force on a charge of 1micro microcoulomb placed at the centre of a square?
(Ans: zero)
Conclusion
We conclude that the chapter electric charges and fields has many important concepts. In this article, we covered Electric Flux, Gauss’s Law and all other important concepts from the chapter along with solved and previous year questions. Students can test their knowledge with the help of practice questions.
FAQs on NEET Important Chapter - Electric Charges and Fields
1. Is Electric Charges and Fields important for the JEE/NEET exam?
Yes, the electric charges and fields chapter is one of the important chapters for JEE and NEET exams. It carries around 1-2 questions in NEET which carry around 2% marks. Due to the formula related questions from this chapter it becomes easy to solve and secure marks in the exams.
2. Is the electric charges and fields chapter tough?
No, the electric charges and fields chapter is easy to understand. If you understand the concepts discussed in this chapter, and practice related questions then you can successfully attempt the questions asked from this chapter in both NEET and JEE exams.
3. Can I crack NEET by solving the previous years’ questions?
According to experts, applicants who practice previous year's papers for JEE and NEET have a good probability of passing the exam. Anyway, practice is the key to success. Students must focus on solving methods and study conceptually along with the PYQ’s.























