




Electromagnetic Induction - An Important Concept for NEET
From previous chapters, we know that current produces magnetic fields. Is the reverse of this true? Can a magnetic field produce electric current? The answer is yes. For a very long time, electricity and magnetism were considered a separate field but it is now known that they are interrelated.
It is found that currents are produced in closed coils when placed in a varying magnetic field. The phenomenon in which current is induced by a changing magnetic field is known as Electromagnetic Induction. The current thus produced is called the induced current. If the current is produced, it must be due to some emf produced in the circuit, which is known as induced emf.
In this chapter, students will learn about the central principle of electromagnetic induction i.e. Faraday’s laws. Students will also learn about Lenz's law, which helps to predict the direction of induced current.
Going further in this chapter, students will also learn about the construction and working of devices based on electromagnetic induction such as power generators, dynamos, transformers, etc.
Now, let us move on to the important concepts and formulae related to the NEET exam along with a few solved examples.
Important Topics of Electromagnetic Induction
Electromagnetic Induction
Magnetic Flux
Faraday’s Law
Lenz’s Law
Motional Electromotive Force
Self-inductance
Mutual Inductance
Growth and Decay of Current in an L-R Circuit
Oscillations in L-C Circuit
Important Concepts of Electromagnetic Induction
List of Important Formulae
Solved Examples
1. The current in a long current carrying wire is I = 2t. A conducting loop is placed to the right of this wire. Find magnetic flux $\phi_B$ passing through the loop.
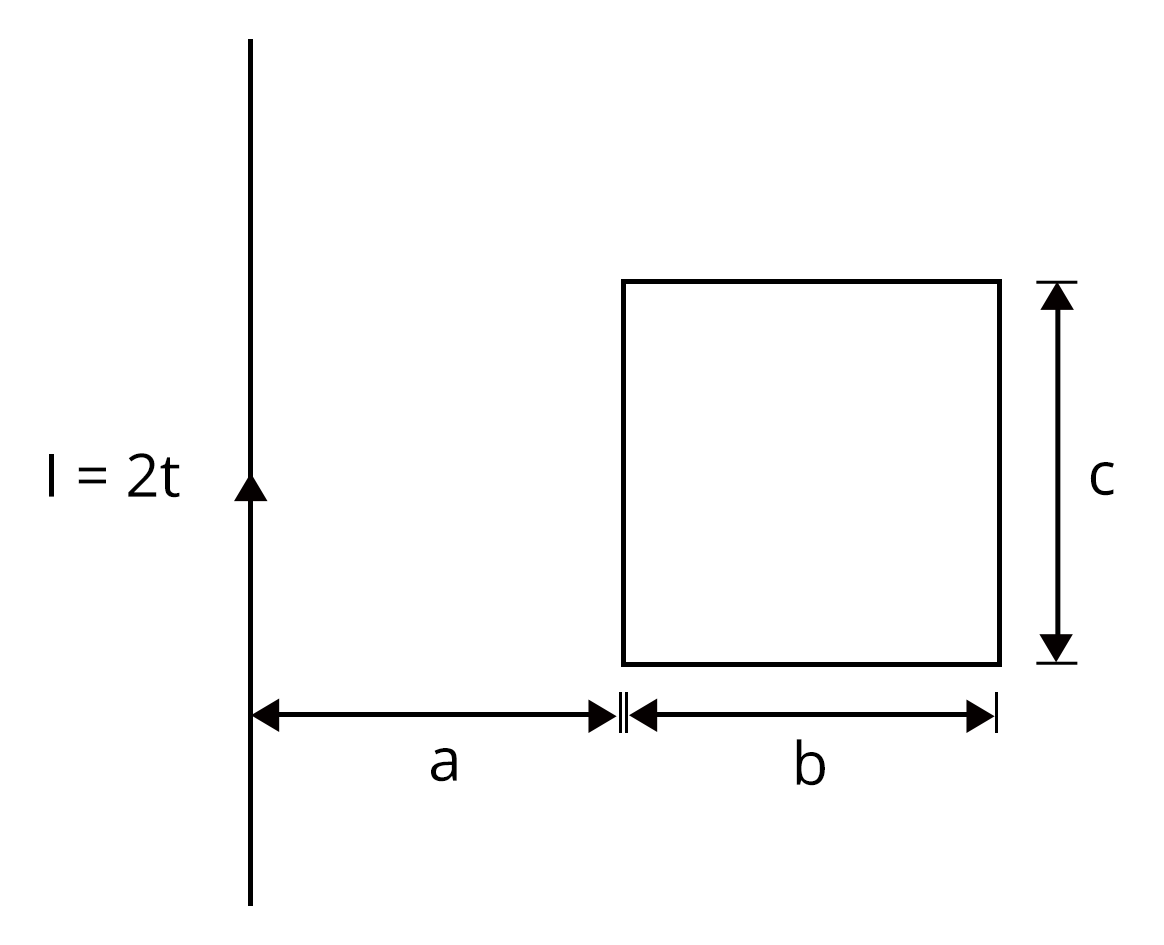
Sol:
In this situation, there is no motion of the conductor and the magnetic field changes with the distance from the current carrying conductor. So, the magnetic flux will be obtained by using an integration method.
Consider an element of thickness, dx at a distance x from the wire as shown in the figure.
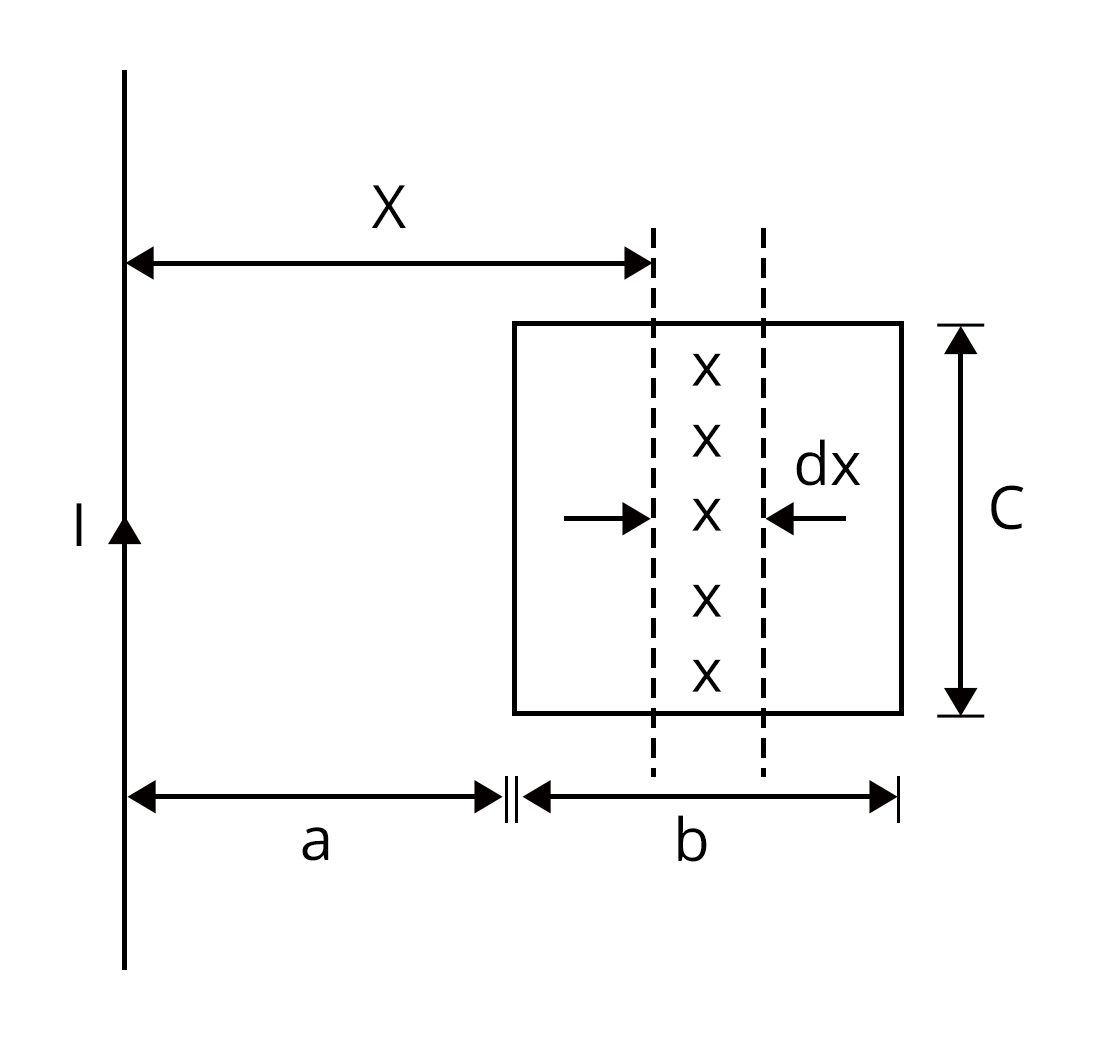
At distance, x magnetic field (B) is
$B = \dfrac{\mu_0}{2\pi}\dfrac{I}{x}$
Now, let us find the area of the strip
$dS = c(dx)$
Therefore, a small magnetic flux passing through the loop will be
$d\phi_B= BdS\cos0°$
$d\phi_B= \dfrac{\mu_0}{2\pi}\dfrac{I}{x}cdx$
The total magnetic flux is
$\phi_B= \int_{a}^{a+b} d\phi_B$
$\phi_B= \int_{a}^{a+b} \dfrac{\mu_0Ic}{2\pi}\dfrac{dx}{x}$
$\phi_B=\dfrac{\mu_0Ic}{2\pi}\ln\lgroup\dfrac{a+b}{a}\rgroup$
Also, it is given that I = 2t
$\phi_B=\dfrac{\mu_0Itc}{\pi}\ln\lgroup\dfrac{a+b}{a}\rgroup$
Hence, the magnetic flux passing through the loop is $\dfrac{\mu_0Itc}{\pi}\ln\lgroup\dfrac{a+b}{a}\rgroup$
Key point: In such cases where there is no motion and magnetic field is varying as a function of distance, the integration method comes in handy.
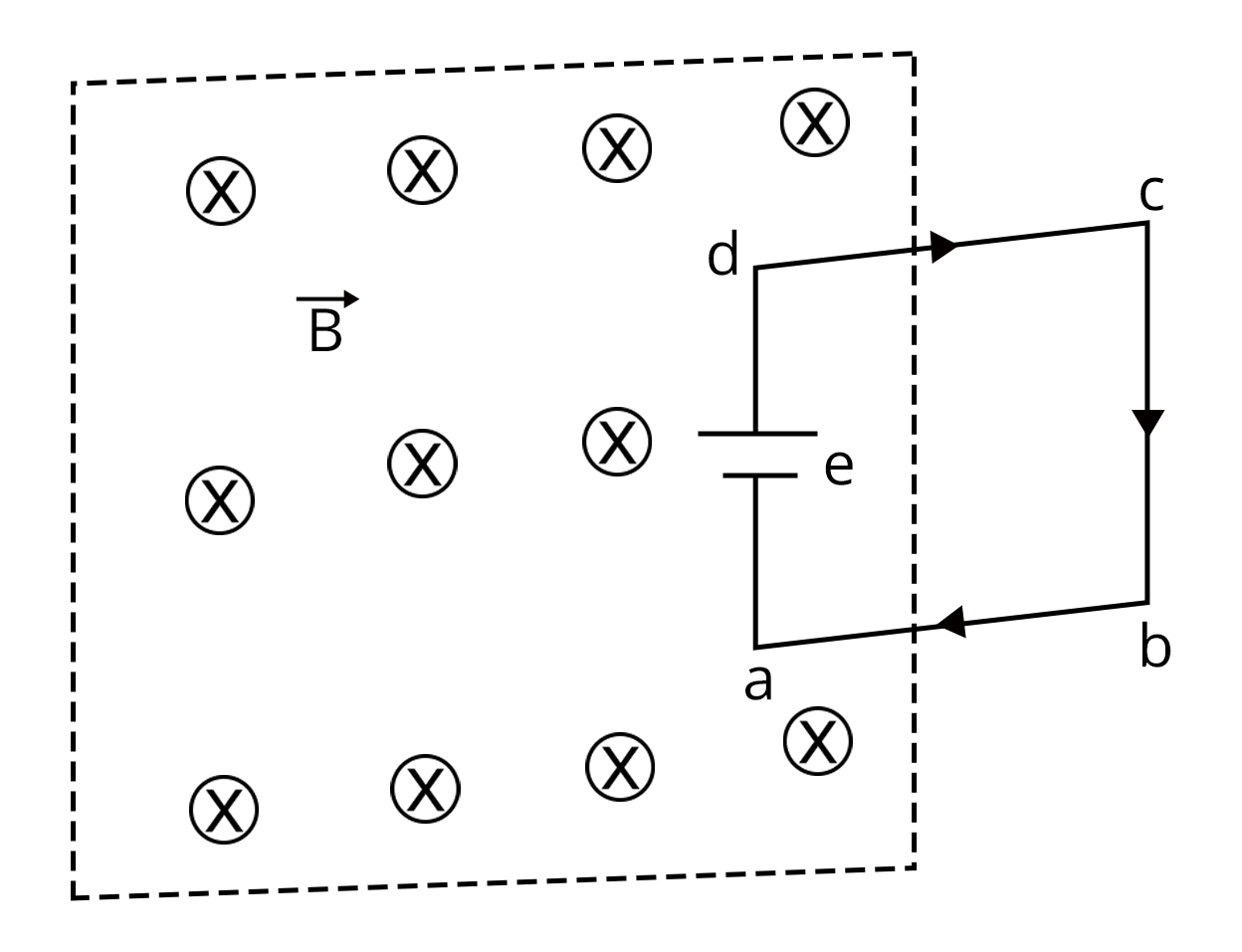
2. A square loop of side l having resistance R moves with constant velocity v, through a constant magnetic field as shown in figure. Find the magnitude and direction of induced current in the situation when
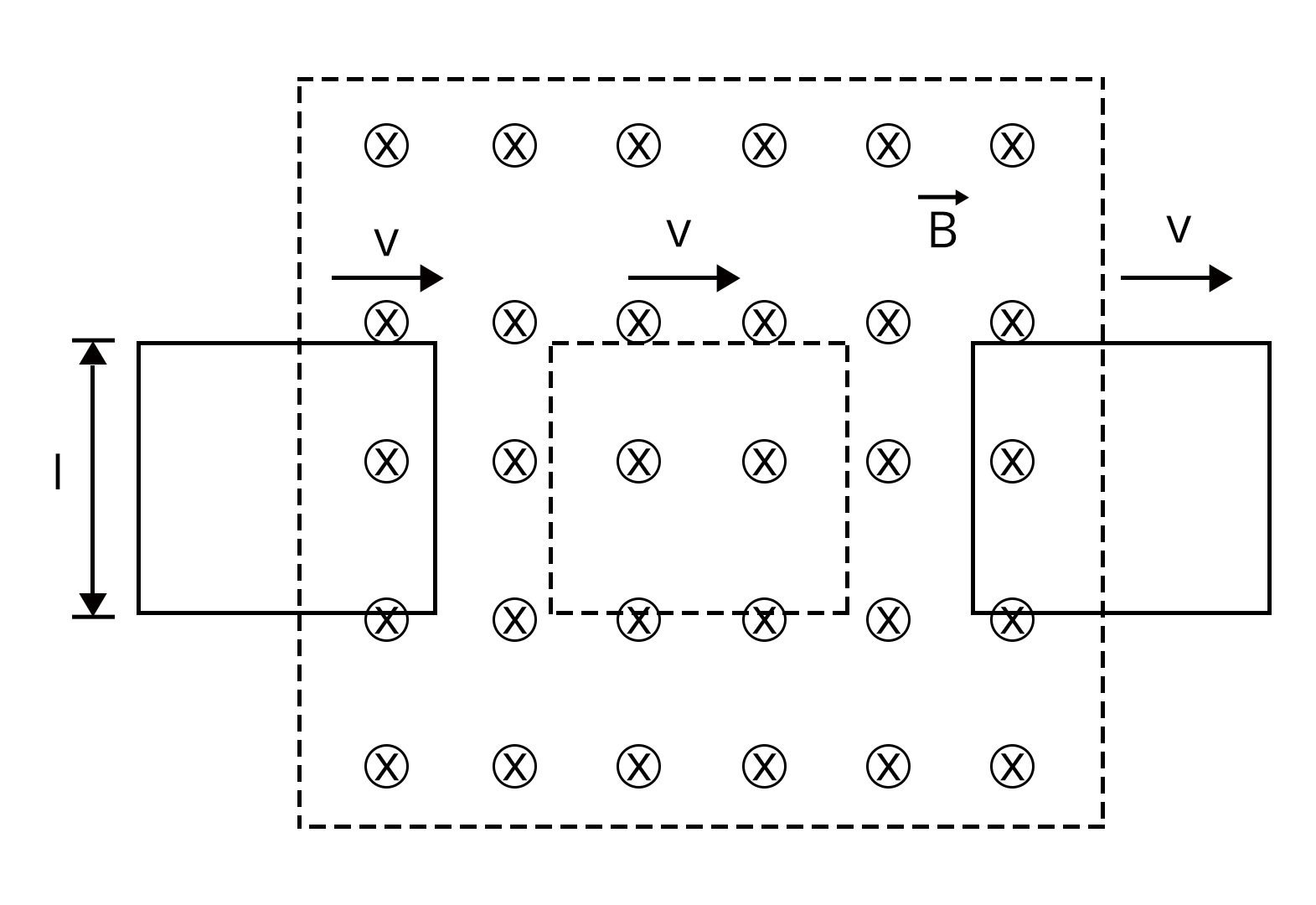
The loop enters into the magnetic field.
It is moving in a magnetic field.
It is coming out of the magnetic field.
Sol:
1. Here the side ad is outside the field. Therefore, no magnetic flux will be induced in side ad. Now, sides ab and cd are parallel to the velocity of the loop and no current is induced when the velocity is parallel to the velocity of the loop. So, the emf will only be induced in the side cb as shown in figure.
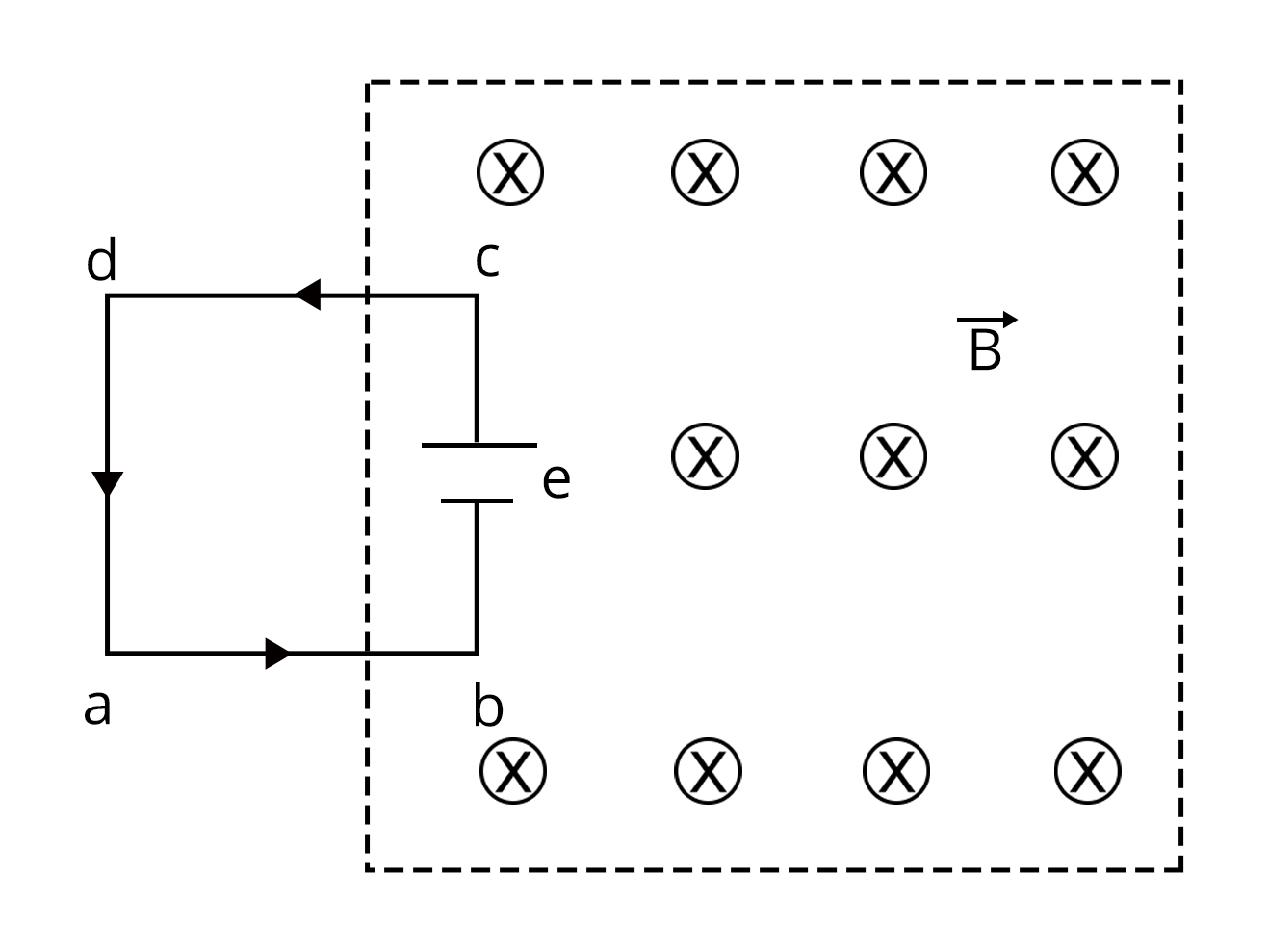
Hence, net emf induced will be $\varepsilon= Blv$
The current in the loop $I = \dfrac{\varepsilon}{R}$ = $\dfrac{Blv}{R}$. The current will be counterclockwise
2. When the loop is completely submerged in the field, there is no change in the flux w.r.t. time. So, there will not be an induction of current.
3. When the loop starts coming out of the magnetic field. The emf will be induced in side ad only. Using Lenz’s law, the direction of current will be clockwise.
Hence, the net emf induced will be $\varepsilon= Blv$
The current in the loop $I = \dfrac{\varepsilon}{R}$ = $\dfrac{Blv}{R}$.
Key Point: Always use Lenz’s law to find the direction of induced current.
Previous Year Questions from NEET Paper
1. The magnetic flux linked with a coil (in Wb) is given by the equation $\phi= 5t^2+3t+16$. The magnitude of induced emf in the coil at the fourth second will be (NEET 2020)
33 V
43 V
108 V
10 V
Sol:
The magnetic flux linked with the coil is given as
$\phi= 5t^2+3t+16$
The magnitude of the induced emf is
$e= \dfrac{\text{d}\phi}{\text{d}t} = e = \dfrac{d}{dt}5t^2+3t+16$
At t = 3s, $e_3$ = 33V,
At t = 4s, $e_4$ = 43V,
Therefore, the induced emf will be:
$e= e_4-e_3$ = 10 V
Hence, the correct answer is option (d)
Trick: The rate of change of magnetic flux is emf induced in the conductor.
2. A wheel with 20 metallic spokes, each 1 m long, is rotated with the speed of 120 rpm in a plane perpendicular to a magnetic field of 0.4 G. The induced emf between axle and rim of the wheel will be (1G = $10^{-4}$T) (NEET 2020)
$2.51 \times10^{-4} V$
$2.51 \times10^{-5} V$
$4.0 \times10^{-5} V$
$2.51 V$
Sol:
Given,
Magnetic field (B) = 0.4 G = $0.4 \times10^{-4} T$,
Frequency (f) = 120 rpm = $\dfrac{120}{60}$ rps = 2 Hz,
The induced emf between the axle and the rim of the wheel is given as
$|e|= \dfrac{1}{2}Bl^{2}\omega$
$|e|= \dfrac{1}{2}Bl^{2}(2\pi f)$ = $2.51 \times10^{-4} V$
Option (a) is the correct answer.
Trick: Rotational emf is given by $|e|= \dfrac{1}{2}Bl^{2}\omega$
Practice Questions
1. A coil formed by wrapping 50 turns of a wire in the shape of a square is positioned in a magnetic field so that the normal to the plane of the coil makes an angle of 30°, with the direction of the field. When the magnetic field is increased uniformly from 200 µT to 600 µT in 0.4 s, an emf of magnitude 80.0 mV is induced in the coil. What is the total length of the wire? (Ans. 272 m)
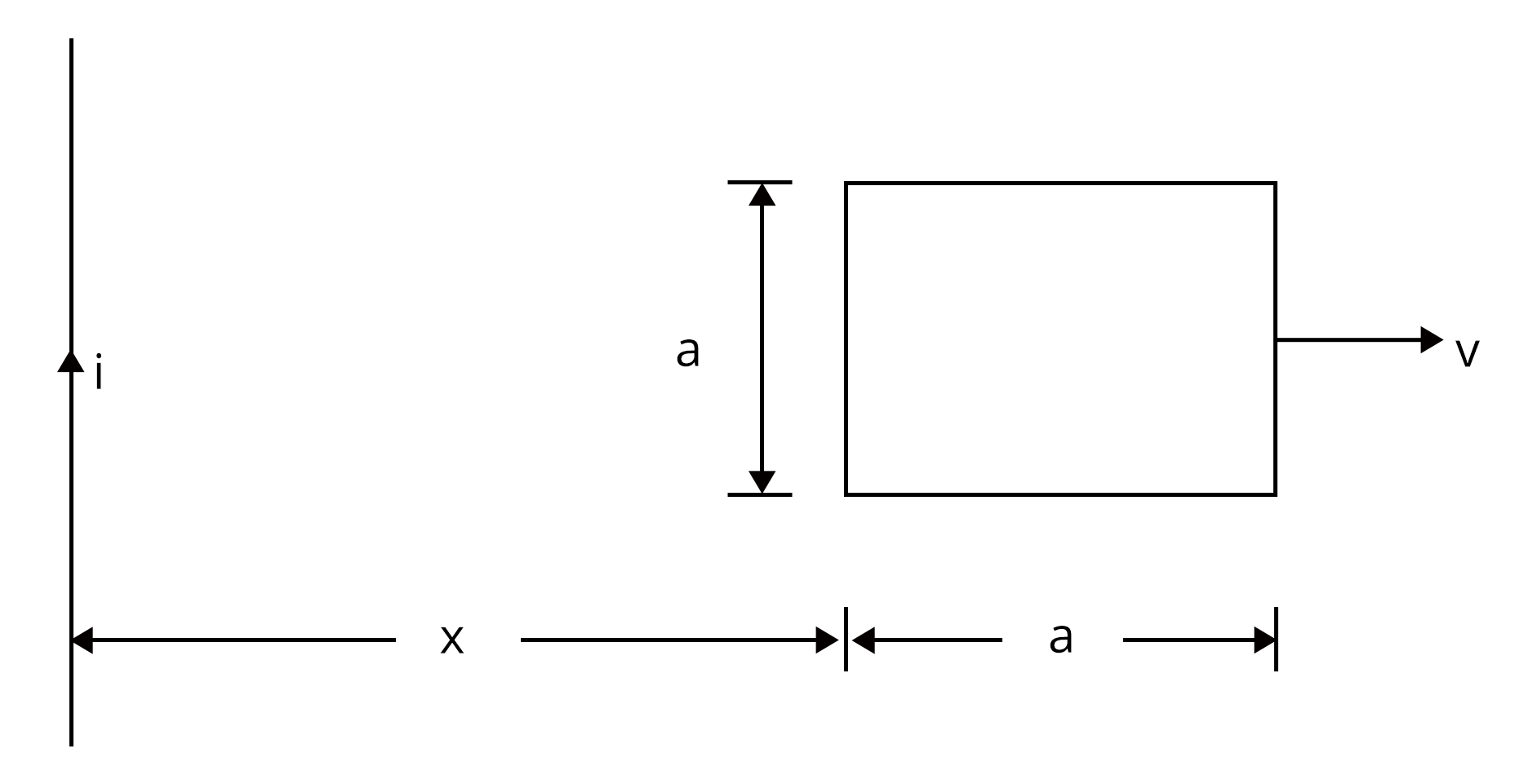
2. A square frame with side a and a long straight wire carrying a current i are located in the same plane as shown in the figure. The frame translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x. (Ans. $e = \dfrac{\mu_0}{4\pi}\dfrac{2ia^2v}{x(x+a)}$ )
Conclusion
In this article, we have provided important information regarding the chapter Electromagnetic Induction such as important concepts, formulae, etc. Students should work on more solved examples for securing good grades in the NEET 2026 exam.
FAQs on NEET Important Chapter - Electromagnetic Induction
1. What is the weightage of the Electromagnetic Induction in NEET?
Nearly 2-3 questions arise in the exam from this chapter almost every year. Hence, students should definitely lay more emphasis on the chapter of Electromagnetic Induction.
2. What are the key points that need to be practised for solving questions from Electromagnetic Induction?
Students should concentrate on understanding Faraday’s and Lenz’s law thoroughly while practising for solving questions from Electromagnetic Induction.
3. Are previous year questions enough for NEET?
To score 640+ in NEET, NCERT (both 11th and 12th) and previous year NEET papers are sufficient. Solving previous 10 years NEET examination papers offers a tremendous advantage because 6-7 questions with identical alternatives are guaranteed to be repeated every year.























