NEET Important Chapter - Electrostatic Potential and Capacitance

In this chapter we understand how we move the charge in this field and what amount of work is done to move the charge against this field and in what form the work done is stored in the system and what is electrostatic potential.

In this chapter we first define electrostatic potential and then potential due to  a point charge, system of charges, electric dipole and potential energy of charges and dipole in an external field. We got introduced to new concepts like equipotential surface, electrostatics of conductors, dielectric and polarization etc. and define electrostatic potential energy.

In this chapter students also get to learn about the capacitors and capacitance and the effect of dielectric medium on it and their combination circuits and electrostatic potential and capacitance all formulas.

Now, let us move on to the important concepts and formulae related to NEET 2022 exams along with a few solved examples.

Important Topics of Electrostatic Potential and Capacitance 

• Electrostatic Potential and Capacitance Notes

• Equipotential Surface

• Capacitor and Capacitance

• Energy Stored in a Capacitor

• Series Combination of Capacitors

• Electrostatic Potential

• Capacitors in the Parallel Combination

• Parallel Plate Capacitor Derivation

• Potential Energy of System of Charges

Important Concepts of Electrostatic Potential and Capacitance

List of Important Formulae

Solved Examples 

1. A parallel plate capacitor with air between the plates has a capacitance of 8pF (1pF = $10^{-12}$ F. What will be the capacitance if the distance between the plates is reduced by half and the space between them is filled with a substance of dielectric constant 6?

Sol: 

Given, Capacitance, C = 8pF = $c = 8\times10^{-12}$F

As per the question In the first case, the parallel plates are at a distance ‘d’ and  

We know that air has dielectric constant, k = 1 so capacitance in first case

Capacitance - $c=\dfrac{A\varepsilon_0}{d}$

Here A = area of the plates

ϵo = permittivity of free space

Now, according to the question if the distance between the plates is halved then   

$d_1$= d/2

Given, dielectric constant of the substance,$K_1$ = 6

Hence, the capacitance of the capacitor-

$c_1=\dfrac{K_1A\varepsilon_0}{d_1} = \dfrac{12A\varepsilon_0}{d}$

By solving this we get 

C1 = 96 PF

Key point: If a parallel plate capacitor is placed in any medium with dielectric constant k then its capacitance is increased by k times.

2. A regular hexagon of the side 10 cm has a charge 5 µC at each of its vertices. Calculate the potential at the center of the hexagon.

Sol: The given figure shows a regular hexagon with charges at each vertex.

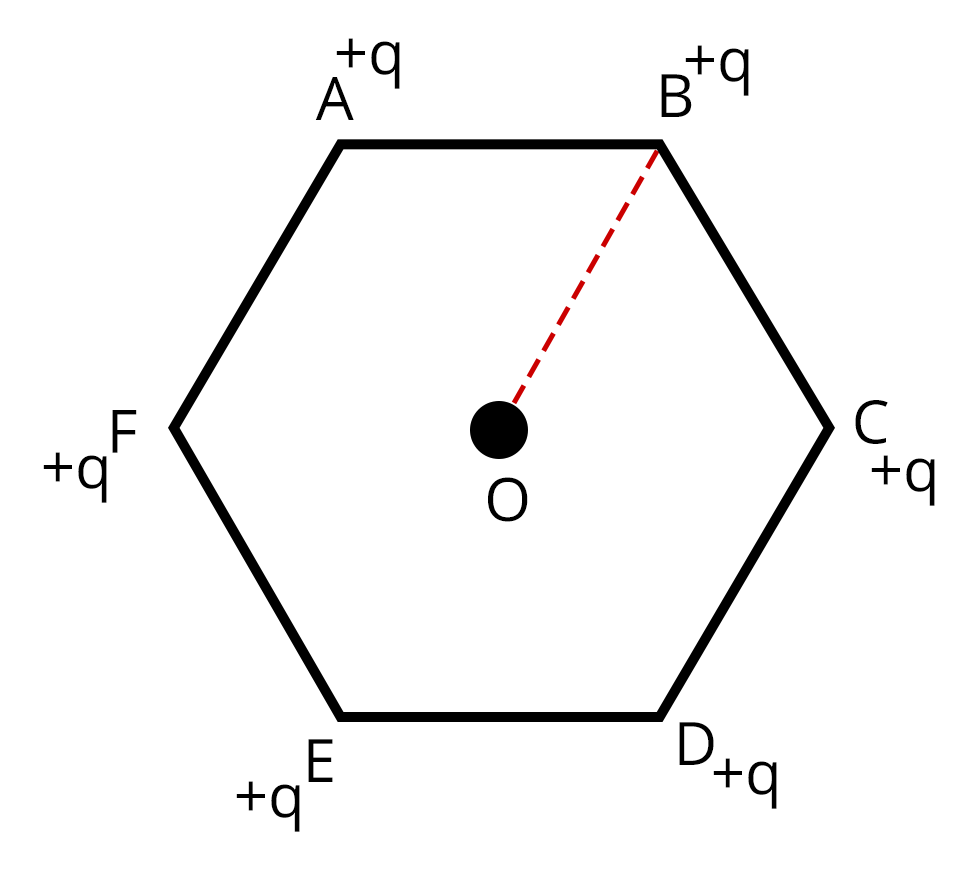
Here, given - q =  5 µC = $5\times10^{-6}$

AB =BC = CD = DE = EF = FA = side of hexagon = 10 cm.

By the diagram the distance of the vertices from the center O, r = 10 cm.

The electric potential at point O,

$V = \dfrac{6q}{4\pi\varepsilon_or}$

Here,​

$k = \dfrac{1}{4\pi\varepsilon_o}$

εo = Permittivity of free space and 

$V = \dfrac{6\times 9✕10^6✕5 ✕10^-6}{0.1} = 2.7 × 10^6 V.$

Trick: If we have symmetry in the shape then we just determine the potential due to a single charge and then multiply it with the total number of charges there are in the system.

Previous Year Questions from NEET Paper

1. The equivalent capacitance of the combination shown in the figure is- (NEET 2021)

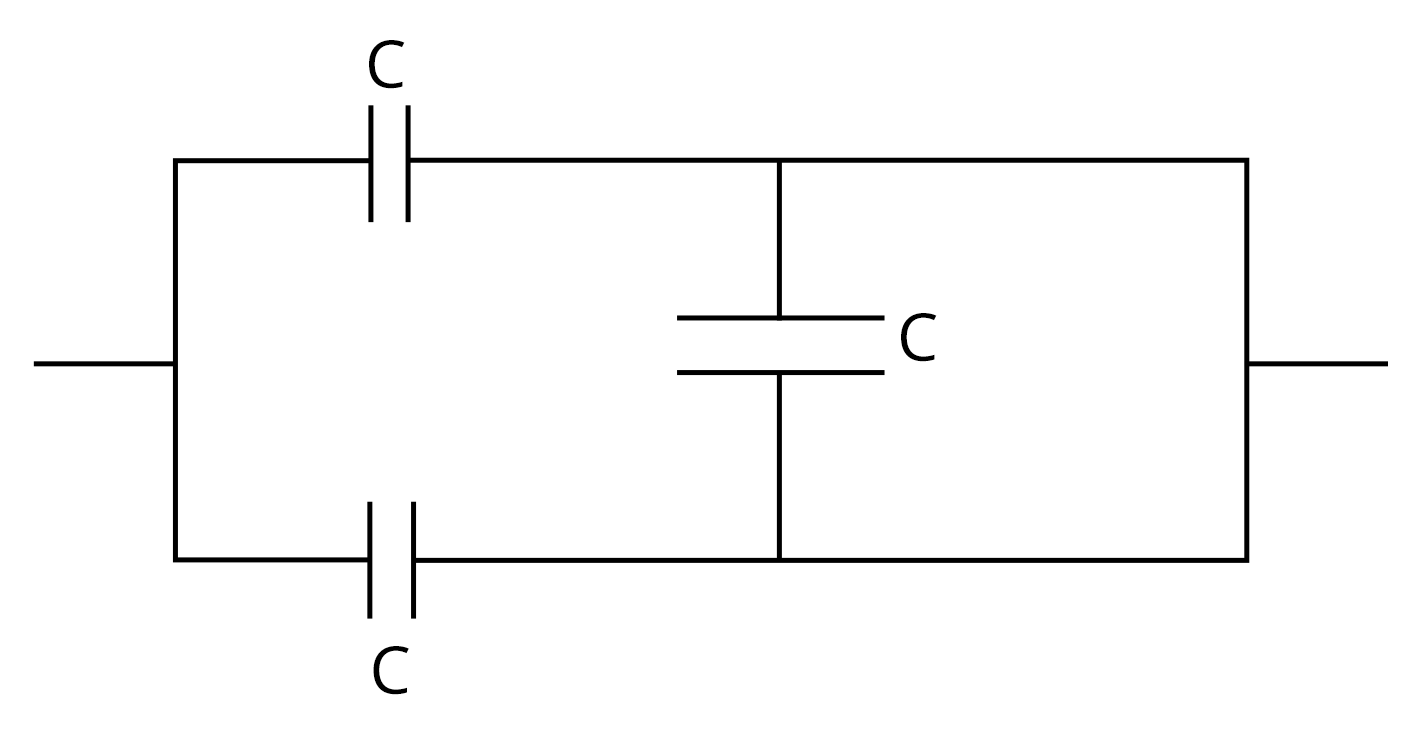
(a) 3C

(b) 2C

(c) C/2

(d) 3C/2

Sol: In the above figure the capacitor in the right side mesh is not contribute in the equivalent capacitance because there is same potential across the both terminal of the capacitor so no current flow through it therefore only capacitors which is in the left mesh is considered and they are in parallel combination so equivalent capacitance would be

Ceq = C + C = 2C

Option (b) is the correct option.

Key point - Current is flow due to potential difference.

2. In a certain region of pace ith volume 0.2 $m^{3}$ , the electric potential is found to be 5 V throughout. The magnitude of electric field in this region is (NEET 2021)

(a) zero

(b) 0.5 N/C

(c) 1 N/C

(d) 5 N/C

Sol: We know the relation between potential and electric field 

$E=-\frac{\text{d}V}{\text{d}r}$

In the given question potential is found to be 5 V throughout the volume (region) so change in potential is zero therefore electric field is also zero in this region.

Option (a) is the correct option.

Trick - Electric field is equal to the potential gradient with negative sign.

Practice Questions

1. If potential (in volts)in a region is expressed as V(,y,z) = 6y - y + 2yz, the electric field (in N/C) at point (1,1,0) is ? (Ans: -$-(6\hat{i}+5\hat{j}+2\hat{k})$)

2. Two capacitors with capacity $C_{1}$ and $C_{2}$ , when connected in series, have capacitance $C_{S}$ and when connected in parallel have capacitance $C_{P}$. find the relation between capacitances ? (Ans: $C_{P}$ $C_{S}$ = $C_{1}$ $C_{2}$)
   

Conclusion

In this article we have provided important information regarding the chapter electrostatic potential formula and capacitance such as important concepts, formulae, etc.. Students should work on more solved examples for securing good grades in the NEET exams.