NEET Important Chapter - Gravitation

The gravitation chapter covers the most important concepts for NEET, JEE and other competitive exams. In the Gravitation chapter, students will study the basic gravitation definition and Newton's law of gravitation.

The chapter on gravitation begins with the very basic definition of gravity, what is gravitation and Newton’s law of gravitation. Further, the chapter covers the concept of acceleration due to gravity and its variations with different parameters. These concepts will lead us to a very important part of the chapter i.e., planetary motion and Kepler's law. In this chapter, we will get to study many interesting and most important concepts such as gravitational constant, gravitational potential, satellites and terms related to satellites, weightlessness and Binding energy.

The concept of the gravitational field will help us in studying the gravitational potential and potential energy where we can see the resemblance with the electrostatic fields. In this article, we will solve many important numerical problems that will help us in acing the exams.

In this article, we will cover the important concepts and topics that will help students to revise and boost their preparations for NEET/JEE.

Important Topics of Gravitation

• Universal law of gravitation

• Acceleration due to gravity

• Variations of acceleration due to gravity

• Kepler’s laws of planetary motion

• Gravitation potential and gravitational potential energy

• Satellites

• Binding energy

• Weightlessness

Important Concepts of Gravitation

List of Important Formulae of Gravitation

Important Questions of Gravitation

1. The change in the value of g at a height h above the surface of the earth is the same as at a depth d below the surface of earth. When both d and h are much smaller then the radius of earth, then which of the following is correct?

1. d = 2h

2. d = h

3. d = $\tfrac{h}{2}$

4. d = $\tfrac{3h}{2}$

Answer: (a)

$\Delta g_{1} = \Delta g_{2}$

$ \Rightarrow g(\frac{2h}{R}) = g\frac{d}{R}$

$\Rightarrow d = 2h

2. The average density of the earth?

(a) is directly proportional to g

(b) is inversely proportional to g

(c) does not depend on g

(d) is a complex function of g

Answer: (a)

Average density of earth = $\frac{3g}{4\pi GR}$

So, Average density of the earth is directly proportional to g.

3. A satellite of the sun is in a circular orbit around the sun, midway between the sun and the earth. Then

(a) The period of the satellite is nearly 229 days

(b)The period of the satellite is nearly 129 days

(c) The speed of the satellite equal the escape velocity of the earth.

(d) The acceleration of the satellite is four times the acceleration of the Earth.

Answer: (b)

$T^{2}\alpha r^{3}$

$\frac{T_{1}}{T_{2}} = (\frac{r}{r/2}^{3/2})$

$\frac{365 days}{T}=2\sqrt{2; }\text{T}\frac{365 days}{2\sqrt{2}} days \Rightarrow 129 days$

4. When you move from equator to pole, the value of acceleration due to gravity (g)

1. Increases

2. Decreases

3. Remains the same

4. Increases then decreases

Answer: (a)

From equation: 

$g^{1} - g - \infty ^{2}R, cos^{2}\lambda$

Where $\lambda$ is the latitude which is $0^{0}$ at the equator and $90^{0}$ at the poles. Therefore $g^{1}$ is maximum at poles and minimum at equator. Hence value of g increases while going from the equator poles. 

5. The weight of the body at the centre of the earth is 

1. Zero

2. Infinite

3. Same as on the surface

4. None of these

Answer: (a)

Because g at centre of the earth is zero so weight = mg is also zero.

Solved Examples of Gravitation

1. An artificial satellite was moving in a circular orbit such that its total energy was 2Eo. Then, calculate the potential energy of the given satellite.

1. E0

2. 3 E0

3. 4 E0

4. -E0

Sol:

Given,

The total energy of the satellite=E=2 Eo

We know that the total energy of the satellite is given by=$E=-\dfrac {G{M_e}m} {2({R_e}+h)}$

Since, Re>>h, we get:

$E=-\dfrac {G{M_e}m} {2{R_e}}$

$E=-\dfrac {G{M_e}m} {2{R_e}}=2 {E_o}$

Now, the potential energy of the satellite is given by:

$U=-\dfrac {G{M_e}m}{R}=2 E=4 {E_o}$

Therefore, the potential energy of the satellite is 4 Eo. Hence, the right option is “c”.

Key Point: The relationship between the total energy and potential energy of the satellite is U=2E.

2. The height at which the acceleration due to gravity becomes $\dfrac {g}{5}$ in terms the radius of the earth R, is

1. $\dfrac {R}{3}$

2. 2R

3. $\dfrac {R}{4}$

4. $\dfrac {2R} {5}$

Sol:

Given,

Acceleration due to gravity at a height “h”=gh=$\dfrac {g}{5}$

Now, we are asked to determine the height h in terms of radius of earth. We know that, variation of acceleration due to gravity with height is given by:

${g_h}=g \left (1- \dfrac {2h}{R_e} \right )$

$\dfrac {g}{5}=g \left (1- \dfrac {2h}{R} \right )$

$h=\dfrac {2R} {5}$

Therefore, option “d” is the right answer.

Key point: Here, the formula of acceleration due to gravity with the variation of height can be used directly.

Previous Year Questions of Gravitation

1. Two stars of masses m and 2m at a distance d rotate about their common center of mass in free space. The period of revolution is: (JEE 2021)

1. $2 \pi \sqrt {\dfrac {d^3}{3Gm}}$

2. $\dfrac{1} {2 \pi} \sqrt {\dfrac {3Gm}{d^3}}$

3. $\dfrac{1} {2 \pi} \sqrt {\dfrac {d^3}{3Gm}}$

4. ${2 \pi} \sqrt {\dfrac {3Gm}{d^3}}$ 

Sol: 

Given,

Two stars of masses m and 2m are placed at a distance of d. Now, it is being said that they are rotating about their own axis in free space. We know that these two stars are able to rotate in a circular motion due to the force of attraction (gravitational attraction). Then we need to determine the center of mass for these two distances.

We know that, center of mass can be calculated by using below equation:

$C.O.M=\dfrac {{m_1}{x_1}+{m_2}{x_2}} {{m_1}+{m_2}}$

Let us assume that we are considering m as the initial position of the system then we get:

$C.O.M=\dfrac {{m}{(0)}+{2m}{d}} {{m}+{2m}}$

$C.O.M=\dfrac {2d}{3}$

So, now the force due to gravity acting between the two stars will be equal to the centripetal force acting towards the C.O.M. We write:

$\dfrac {Gm(2m)}{d^2}= m \left (\dfrac {2d}{3} \right ){\omega^2}$

${\omega^2}=\dfrac {3Gm}{d^3}$

$T=2\pi \sqrt {\dfrac {d^3}{3Gm}}$

Therefore, option A is the right answer.

Trick: The C.O.M is considered as a static point, thus the masses will always rotate about the same axis.

2. Consider two solid spheres of radii R1 = 1m, R2 = 2m and masses M1 and M2, respectively. The gravitational field due to sphere (1) and (2) are shown. The value of $\dfrac {M_1}{M_2}$ is : (JEE main 2020)

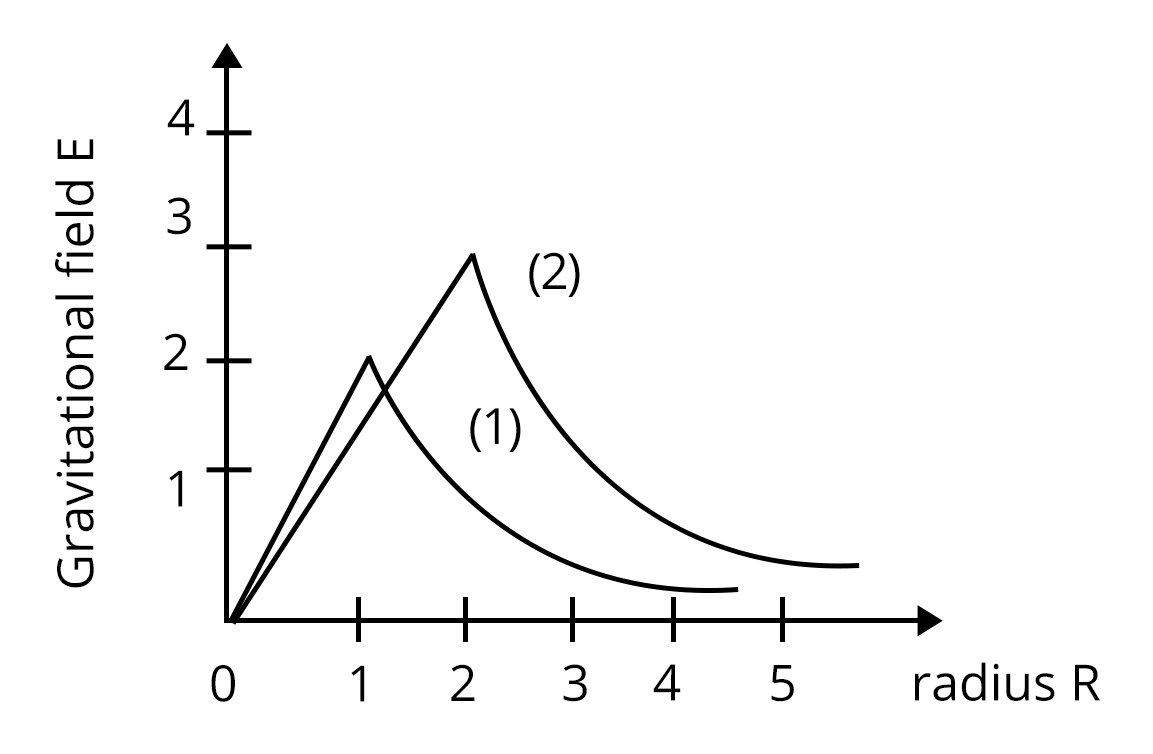
1. $\dfrac {2}{3}$

2. $\dfrac {1}{6}$

3. $\dfrac {1}{2}$

4. $\dfrac {1}{3}$

Sol:

Given,

The radii of the two spheres are R1 = 1m, R2 = 2m and masses M1 and M2, respectively. We are asked to determine the ratio of the masses. From the gravitational field equation, we know that:

$E=\dfrac {GM}{R^2}$

For given two spheres we get:

${E_1}=\dfrac {G{M_1}}{{R_1}^2}$

${E_2}=\dfrac {G{M_2}}{{R_2}^2}$

The ratio of masses will be:

$\dfrac {E_1}{E_2}=\dfrac {{M_1}{R_2}^2}{{M_2}{R_1}^2}$

$\dfrac {2}{3}=\dfrac {2^2}{1^2} \dfrac {M_1}{M_2}$

$\dfrac {M_1}{M_2}=\dfrac {1}{6}$

Therefore, the right answer is option b.

Trick: We used the graphs to know the value of gravitational fields instead of using the formula for determining the value of the gravitational field.

Practice Questions

1. A straight rod of length L extends from x = a to x = L + a. The gravitational force it exerts on a point mass 'm' at x = 0, if the mass per unit length of the rod is A + Bx2, is given by? 

Ans: $ GM\left [A\left (  \dfrac {1}{a}-\dfrac{1}{a+L}\right )+BL  \right ]$

2. If the Earth has no rotational motion, the weight of a person on the equator is W. Determine the speed with which the earth would have to rotate about its axis so that the person at the equator will weigh $\dfrac {3}{4}$ W. Radius of the Earth is 6400 km and g=10 m/s2.

Ans: $0.63 \times {10^-3} rad/sec$

Conclusion

We conclude that the chapter gravitation has many important concepts that will help us in scoring better marks in NEET and JEE. In this article, we covered gravitation introduction, principles of gravity and all other important concepts from the chapter along with solved and previous year questions. Students can test their knowledge with the help of practice questions.