NEET Important Chapter - Magnetism and Matter

Magnetism and matter is one of the easiest and smallest chapters in Physics for the NEET exam. In magnetism and matter, we deal with magnetic dipoles and their properties in detail along with earth’s magnetism. Students can easily score good marks from this chapter for the NEET 2022 exam compared to other chapters. 

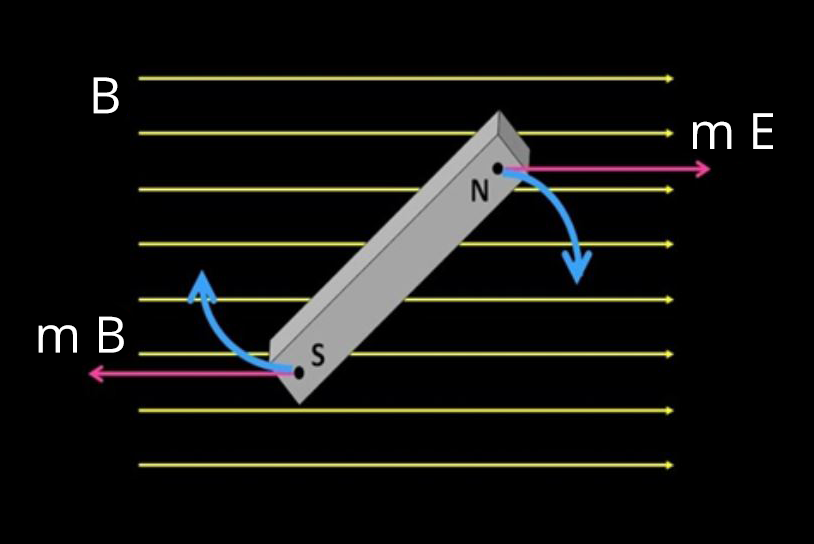
The magnetism and matter chapter starts with magnetic dipoles and calculating the dipole moment of a magnetic dipole. Various terms related to magnetism like magnetic field lines, magnetising field, the intensity of magnetisation, etc. are discussed in this chapter. The formula to calculate the torque and potential energy of a bar magnet placed in an external magnetic field is also studied in this chapter.

In this chapter, we also learn what are the three elements of the earth's  magnetic field. Materials are classified according to their magnetic properties like paramagnetic, diamagnetic and ferromagnetic. Curie's law and its equation are discussed in this chapter along with the hysteresis curve of ferromagnetic materials. 

Now, let us move on to the important concepts and formulae related to NEET exams from magnetism and matter along with a few solved examples.

Important Topics of Magnetism and Matter

• Magnetic dipole moment of a magnet

• Terms related to magnetism

• Elements of Earth’s Magnetic Field

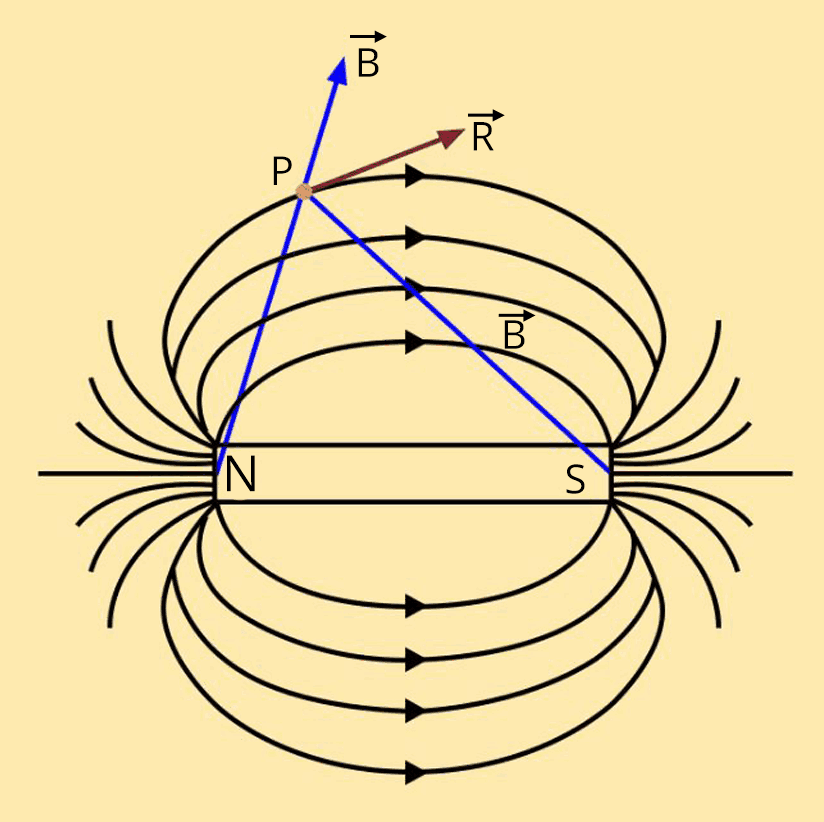
• Magnetic Dipole Moment

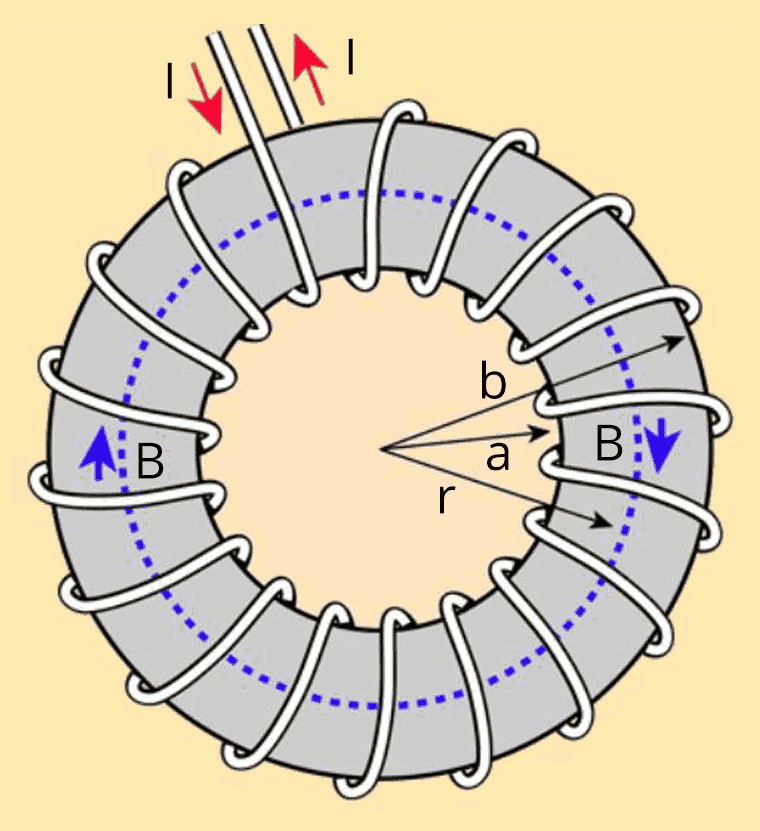
• Magnetic Materials

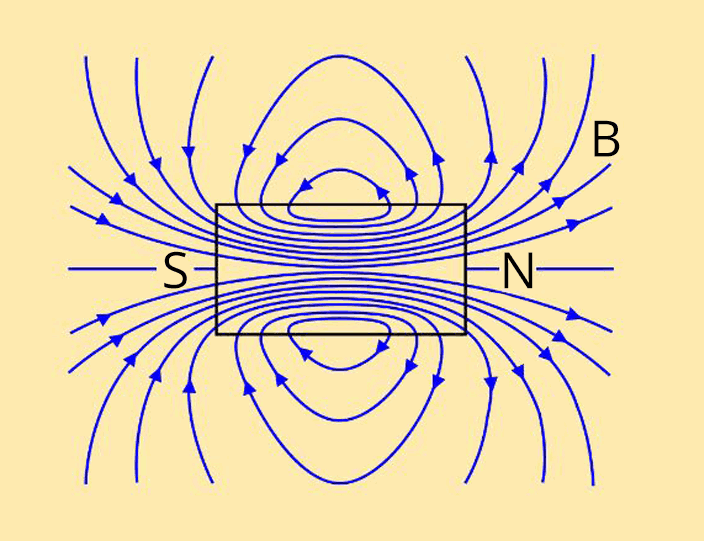
• Magnetic field lines and their properties 

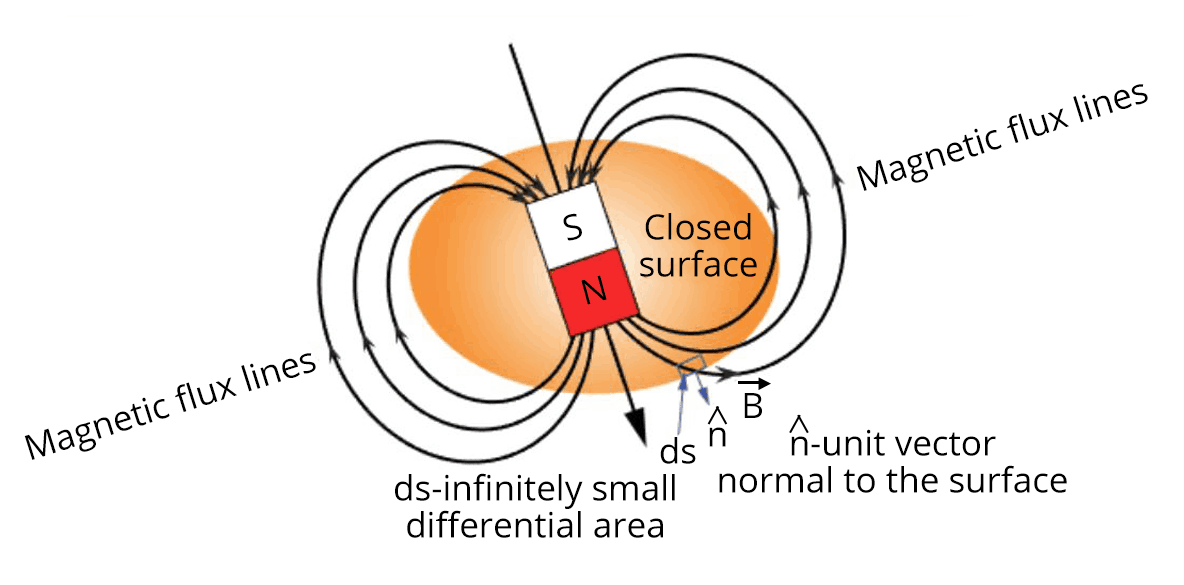
• Gauss’s Law of Magnetism

• Hysteresis curve

• Curie’s Law

Important Concepts of Magnetism and Matter

List of Important Formulae

Solved Examples 

1. A magnetic needle lying parallel to a magnetic field requires W  units of work to turn it through 60o. The torque required to maintain the needle in this position in terms of W will be

Sol:

The work done to rotate the magnetic needle when it is parallel to the magnetic field to an angle of 600 can be calculated using the formula given below.

$ W = MB(\cos\theta_1-\cos\theta_1)$

$ W= MB(\cos0^o-\cos60^o)$

$W= \dfrac{MB}{2}$....(1)

The torque required to maintain the needle can be calculated using the formula given by

$ \tau = MB\sin\theta$

$ \tau = MB\sin60^o$

$ \tau = \dfrac{\sqrt{3}MB}{2}$....(2)

Divide equation (2) by equation (1) to get the torque in terms of W.

$\dfrac{\tau}{W}=\dfrac{\dfrac{\sqrt{3}MB}{2}}{\dfrac{MB}{2}}$

$\tau=\sqrt{3}W$

Key Point: To maintain the needle placed in a magnetic field at a particular position, an equal and opposite torque experienced by the needle has to be applied to it.

2. If the angle of dip at two places are 300 and 450 respectively, then the ratio of the horizontal components of earth’s magnetic field at two places will be  

Sol:

Given:

The angle of dip of two places are θ1= 300 and  θ2=450

The horizontal component of earth’s magnetic field where θ1= 300 is given by

$B_{H1}=B\cos\theta_1$

$B_{H1}=B\cos(30^0)$

$B_{H1}=\dfrac{\sqrt{3}B}{2}$...(1)

Similarly, the horizontal component of earth’s magnetic field where θ1= 450 is given by

$B_{H2}=B\cos\theta_2$

$B_{H2}=B\cos(45^0)$

$B_{H2}=\dfrac{B}{\sqrt{2}}$....(2)

Divide equation (1) by equation (2) to obtain the ratio of horizontal components of earth’s magnetic field.

$\dfrac{B_{H1}}{B_{H2}}=\dfrac{\left(\dfrac{\sqrt{3}B}{2}\right)}{\left(\dfrac{B}{\sqrt{2}}\right)}$

$\dfrac{B_{H1}}{B_{H2}}=\dfrac{\sqrt{3}}{\sqrt{2}}$

Key Point: The horizontal component of earth’s magnetic field and dip angle is related by the formula. 

Previous Year Questions from NEET Paper

1. A magnetic needle suspended parallel to a magnetic field requires √3 J of work to turn it through 600. The torque needed to maintain the needle in this position will be (NEET 2012)

1. 2√3 J

2. 3 J

3. √3 J

4. 3/2 J

Sol: 

The work done to rotate the magnetic needle when it is parallel to the magnetic field to an angle of 600 can be calculated using the formula given below.

$ W = MB(\cos\theta_1-\cos\theta_1)$

$ W= MB(\cos0^o-\cos60^o)$

$\sqrt{3}= \dfrac{MB}{2}$....(1)

The torque required to maintain the needle can be calculated using the formula given by

$ \tau = MB\sin\theta$

$ \tau = MB\sin60^o$

$ \tau = \dfrac{\sqrt{3}MB}{2}$....(2)

Divide equation (2) by equation (1) to calculate the torque.

$\dfrac{\tau}{\sqrt{3}}=\dfrac{\dfrac{\sqrt{3}MB}{2}}{\dfrac{MB}{2}}$

$\tau=\sqrt{3}\times\sqrt{3}$

$\tau=3~\text{J}$

Therefore, correct option is option (b)

Trick: To maintain the needle placed in a magnetic field at a particular position, an equal and opposite torque experienced by the needle has to be applied to it.

2. An iron rod of susceptibility 599 is subjected to a magnetising field of 1200 Am-1. The permeability of the material of the rod is (NEET 2020)

1. 2.4𝜋 ✕ 10-5 TmA-1

2. 2.4𝜋 ✕ 10-7 TmA-1

3. 2.4𝜋 ✕ 10-4 TmA-1

4. 8 ✕ 10-5 TmA-1

Sol: 

The relative magnetic permeability of the material can be calculated using the formula given by

$\mu_r=1+\chi_m$

$\mu_r=1+599$

$\mu_r=600$

The permeability of the material is calculated by the following formula.

$\mu=\mu_r\mu_0$

$\mu=600\times4\pi\times10^{-7}$

$\mu=2.4\pi\times10^{-4}~TmA^{-1}$

Trick: The relative magnetic permeability is the ratio of magnetic permeability of the material to the magnetic permeability of free space or vacuum.

Practice Questions

1. When a piece of a ferromagnetic substance is put in a uniform magnetic field, the flux density inside it is four times the flux density away from the piece. The magnetic permeability of the material is   (Ans: 4)

2. A short bar magnet of magnetic moment 0.4 JT-1 is placed in a uniform magnetic field of 0.16 T. The magnet is in stable equilibrium when the potential energy is (Ans: 0.064J)

Conclusion

In this article, we have provided important information regarding the chapter Magnetism and Matter, such as important concepts, formulae, etc. Students should work on more solved examples along with  previous year question papers for scoring good grades in the NEET exams.