NEET Important Chapter - Moving Charges and Magnetism

The chapter moving charges and magnetism deals with the magnetic field produced by the current-carrying wire and the  magnetic force acting on a current-carrying wire and moving charge in a magnetic field. As far as the NEET exam is concerned, problems will be asked related to concepts discussed in the chapter.

The chapter moving charges and magnetism begins with the magnetic force acting on a charged particle moving in a magnetic field. Cyclotron which is a practical application of lorentz force is discussed in this chapter in detail. Biot-Savart law and Ampere’s law are very important concepts in this chapter. 

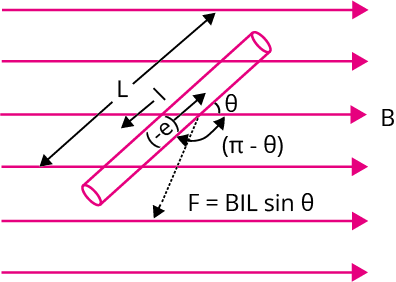
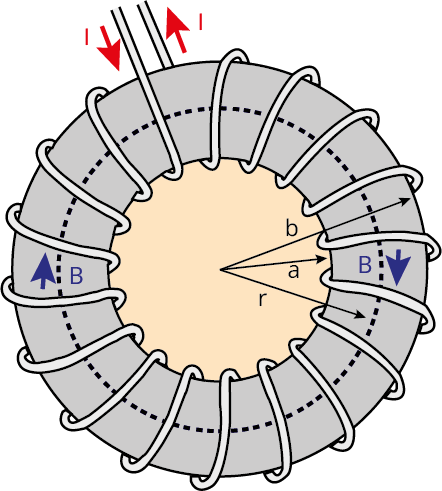
We also learn about the formula of magnetic effect of electric current and magnetic field produced due to a solenoid and toroid. Force acting on a current-carrying conductor placed in a  magnetic field and the force acting between two parallel straight conductors are also discussed in this chapter.

Now, let us move on to the important concepts and moving charges and magnetism  formulas related to the NEET 2022 exam from the chapter moving charge and magnetism along with a few solved examples.

Important Topics of Moving Charges and Magnetism

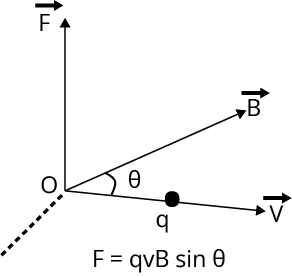
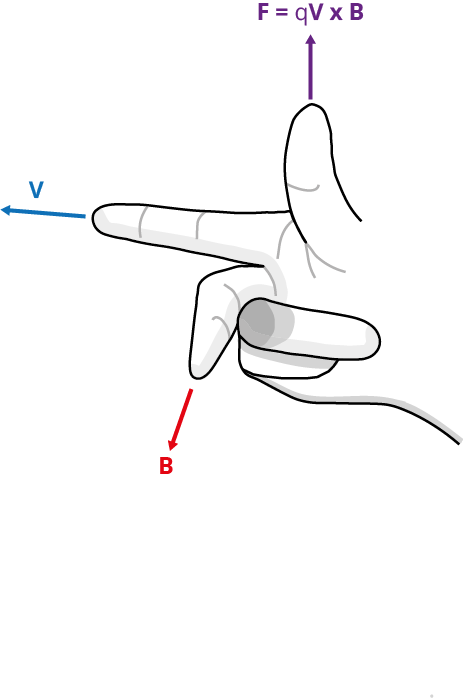
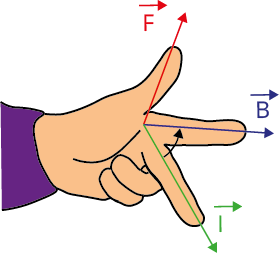
• Magnetic force on a moving charge in a magnetic field

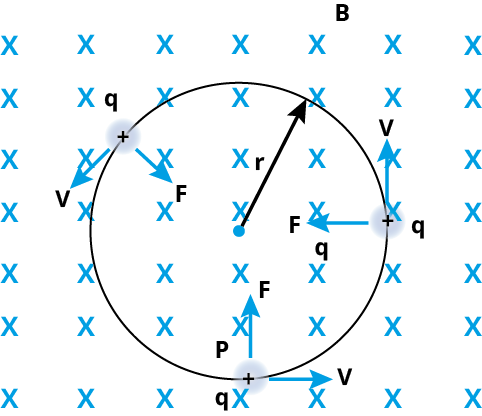
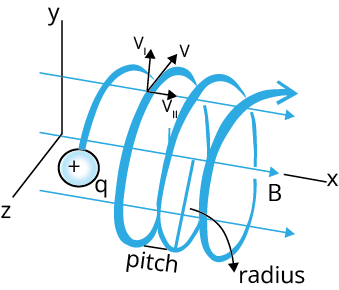
• Trajectory of a charge moving in a perpendicular magnetic field

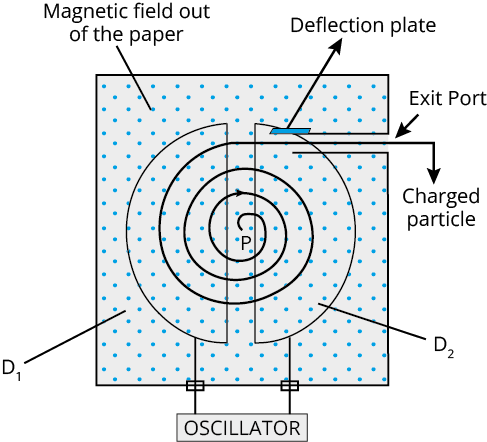
• Cyclotron

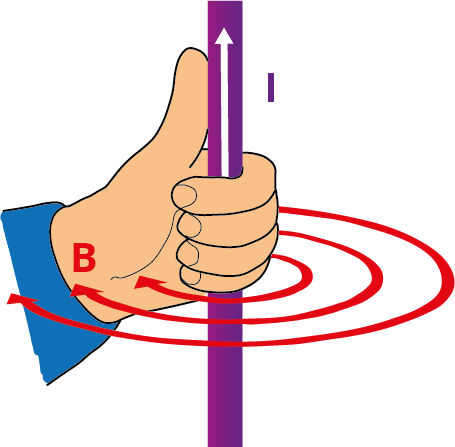
• Biot Savart Law

• Ampere’s Law

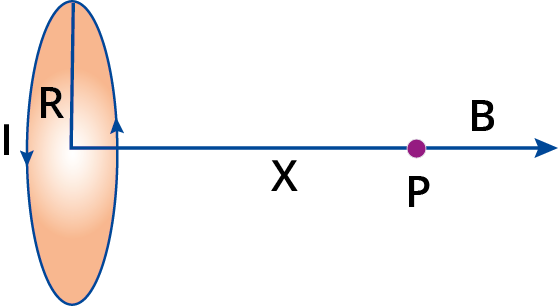
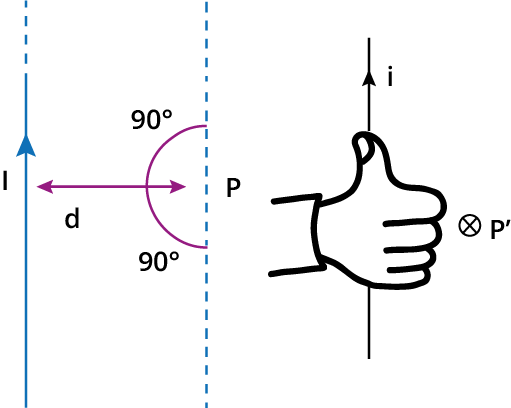
• Magnetic field due to a circular and straight wire

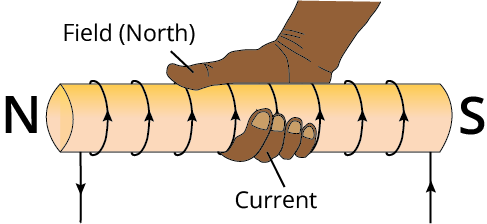
• Magnetic field due to a solenoid

• Force on a current-carrying conductor in a magnetic field.

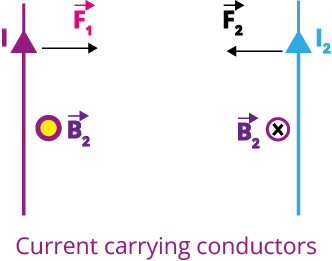
• Force between two parallel current-carrying conductors

Important Concepts of Moving Charges and Magnetism

List of Important Formulae

Solved Examples 

1. Two long parallel wires carrying equal current separated by 1 m, exert a force of 2✕10-7 N/m on one another. The current flowing through them is 

Sol: 

Let the Current passing through each wire be I

The force per unit length acting on each wire is given as 2✕10-7 N/m 

The formula to calculate the force exerted by wires on one another is given by,

$F=\dfrac{\mu_0}{4\pi}\dfrac{2I^2}{d}\times l$

$\dfrac{F}{l}=\dfrac{\mu_0}{4\pi}\dfrac{2I^2}{d}$

$2\times10^{-7}=\dfrac{2\times10^{-7}\times I^2}{1}$

$I=1\text{ A}$

Therefore, the total current flowing through them is 1 A.

Key Point: Force acting between two parallel current-carrying wires depend on the current passing through the wries and distance between them.

2. An alpha particle and proton travel with same velocity in a magnetic field perpendicular to the direction of their velocities, find the ratio of the radii of their circular path.

Sol:

Let the mass of the proton and alpha particle be ‘m’ and ‘4m’ respectively. The charge of the alpha particle is two times the charge of the proton.

The formula to calculate the radius of the circular path of proton is given by

$r=\dfrac{mv}{qB}$...(1)

The radius of the circular path of the alpha particle is given by,

$r'=\dfrac{(4m)v}{(2q)B}$

$r'=\dfrac{2mv}{qB}$....(2)

Divide equation (1) by equation (2) to obtain the ratio of radii of their circular path.

$\dfrac{r}{r'}=\dfrac{\left(\dfrac{mv}{qB}\right)}{\left(\dfrac{2mv}{qB}\right)}$

$\dfrac{r}{r'}=\dfrac{1}{2}$

Therefore, the ratio of the radii of thor circular path is 1:2

Key Point: Alpha particle is a He2+ nucleus and has mass four times the mass of a proton and charge equal to double the charge of proton

Previous Year Questions from NEET Paper

1. A 250 turn rectangular coil of length 2.1 cm and width 1.25 cm carries a current of 85 μA and subjected to magnetic field of strength 0.85 T. Work done for rotating the coil by 180o against the torque is (NEET 2017)

1. 4.55 μJ 

2. 2.3 μJ

3. 1.15 μJ

4. 9.1 μJ

Sol: 

The magnetic moment of the rectangular coil is calculated by the formula given below,

$ M=NAI$

$ M=250\times(2.1\times 10^{-2}\times1.25\times 10^{-2})\times85\times 10^{-6}$

$M= 5.58\times 10^{-6}$

Work done in rotating the rectangular coil can be calculated as follows,

$ W = MB(\cos\theta_1-\cos\theta_2)$

$ W = MB(\cos0^o-\cos180^o)$

$ \tau = 5.58\times 10^{-6}\times 0.85 \times(1+1)$

$W=9.1~\mu J$

Therefore, correct option is option (d)

Trick: Magnetic moment of rectangular coil is equal to the product of number of turns, area of the coil and the current passing through the coil.

2. An infinitely long straight conductor carries a current of 5 A as shown. An electron is moving with a speed of 105 m/s parallel to the conductor. The perpendicular distance between the electron and the conductor is 20 cm at an instant. Calculate the magnitude of the force experienced by the electron at that instant. (NEET 2021)

1. 4✕10-20 N

2. 8𝜋✕10-20 N

3. 4𝜋✕10-20 N

4. 8✕10-20 N
   
   

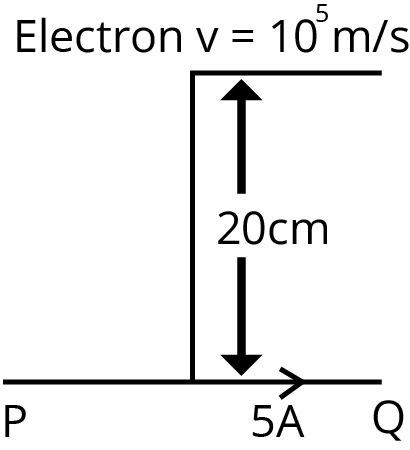
Sol: 

The magnetic field due to current carrying infinitely long straight conductor is given by,

$B=\dfrac{\mu_0I}{2\pi d}$

$B=\dfrac{4\pi\times 10^{-7}\times 5}{2\pi \times20\times10^{-2}}$

$B=5\times 10^{-6}~\text{T}$

The force acting on the electron is given by

$F=qvB$

$F=1.6\times 10^{-19}\times 10^{6}\times5\times 10^{-6}$

$B=8\times10^{-20}~N$

The correct answer is option (d).

Trick: The motion of a charged particle and the magnetic field produced by the infinitely long conducting wire is perpendicular to each other.

Practice Questions

1. A closely wound flat circular coil of 25 turns of wire has diamter of 10 cm which carries a current of 4 A. The flux density at the centre of the coil will be ? (Ans: 1.256✕10-3 T)

2. An electron is moving in a circular orbit of radius r makes n rotations per second. The magnetic field produced at the centre has magnitude_____ (Ans: μ0ne/2r)

Conclusion

In this article we have provided important information regarding the chapter moving charges and magnetism such as important concepts, formulae, etc.. Students should work on more solved examples along with  previous year question papers for scoring good grades in the NEET exam.