NEET 2024 Revision Notes for Electrostatic Potential and Capacitance

Electrostatic potential:

Electrostatic potential at a point can be physically interpreted as the work done by the field in displacing a unit positive charge from some reference point to the given point. Mathematically it is given by,

$V = \dfrac{W}{{{q_0}}}$

Potential at a point is analytically defined as a scalar function of position whose negative gradient at a point gives electric intensity

$\vec E =  - gradV =  - \vec \nabla V =  - \dfrac{{\partial V}}{{\partial x}}\hat i - \dfrac{{\partial V}}{{\partial y}}\hat j - \dfrac{{\partial V}}{{\partial z}}\hat k$

Potential at earth is assumed to be zero as it is a large conductor and its potential is approximately constant with respect to the given charge to it.

Potential Difference:

Potential difference is defined as the amount of work done in moving a unit positive charge from one point to another point. Mathematically,

${V_{ab}} =  - \int\limits_a^b {\vec E.d\vec r}$

Its value does not depend on frame of reference; hence it is an absolute quantity.

As the electric field is conservative, work done and hence potential difference between two points is path independent and depends only on the position of points.

${W_1} = {W_2} = {W_3}$

Electric Potential Due to a Point Charge: Electric potential at a point distance r from a point charge q is $V = \dfrac{q}{{4\pi {\varepsilon _0}r}}$

Electric Potential due to System of Charges: The electric potential at a point due to a system of charges is equal to the algebraic sum of the electric potentials due to individual charges at that point.

$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{{q_1}}}{{{r_1}}} + \dfrac{{{q_2}}}{{{r_2}}} + \dfrac{{{q_3}}}{{{r_3}}} + ......\dfrac{{{q_n}}}{{{r_n}}}} \right) = \dfrac{1}{{4\pi {\varepsilon _0}}}\sum\limits_{i = 1}^n {\dfrac{{{q_i}}}{{{r_i}}}} $

Electric Potential at any Point due to an Electric Dipole:

The electric potential at point P due to an electric dipole is $V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{p\cos \theta }}{{{r^2}}}$

Special cases : 

• Where the point P lies on the axial line of the dipole i.e, θ=${0^0}$.

$\therefore $$V = \dfrac{p}{{4\pi {\varepsilon _0}{r^2}}}$

• When the point P lies on the equatorial line of the dipole, i.e.,  $\theta  = {90^0}$

$\therefore $ V = 0.

Electric Potential due to Uniformly Charged Thin Spherical Shell:

Electric potential due to a uniformly charged spherical shell of uniform surface charge density σ and radius R at a point distant r from the centre of the shell is given as follows:

At a point outside the shell i.e.,  r >> R

$V = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{r}$

At a point on the surface of the shell i.e.,   r = R

$V = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{R}$

At a point inside the shell i.e.,  r << R

$V = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{R}$

Here, $q = 4\pi {R^2}\sigma $

Electric Potential on a Spherical Shell on Radius R

Variation of Electric Field and Potential of the Spherical Shell

Electric Potential due to a Uniformly Charged non Conducting Solid Sphere:

Electric potential due to a uniformly charged non-conducting solid sphere of uniform volume charge density ρ and radius R at a point distant r from the centre of sphere is given as follows:

At a point outside the sphere i.e.,   r > R

$V_{out} = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{r}$

At a point on the surface of the sphere i.e.,   r = R

$V_s = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{R}$

At a point inside the sphere i.e.,     r < R

$V_c = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{{q\left( {3{R^2} - {r^2}} \right)}}{{2{R^3}}}$

Here $q = \dfrac{4}{3}\pi {R^2}\rho $

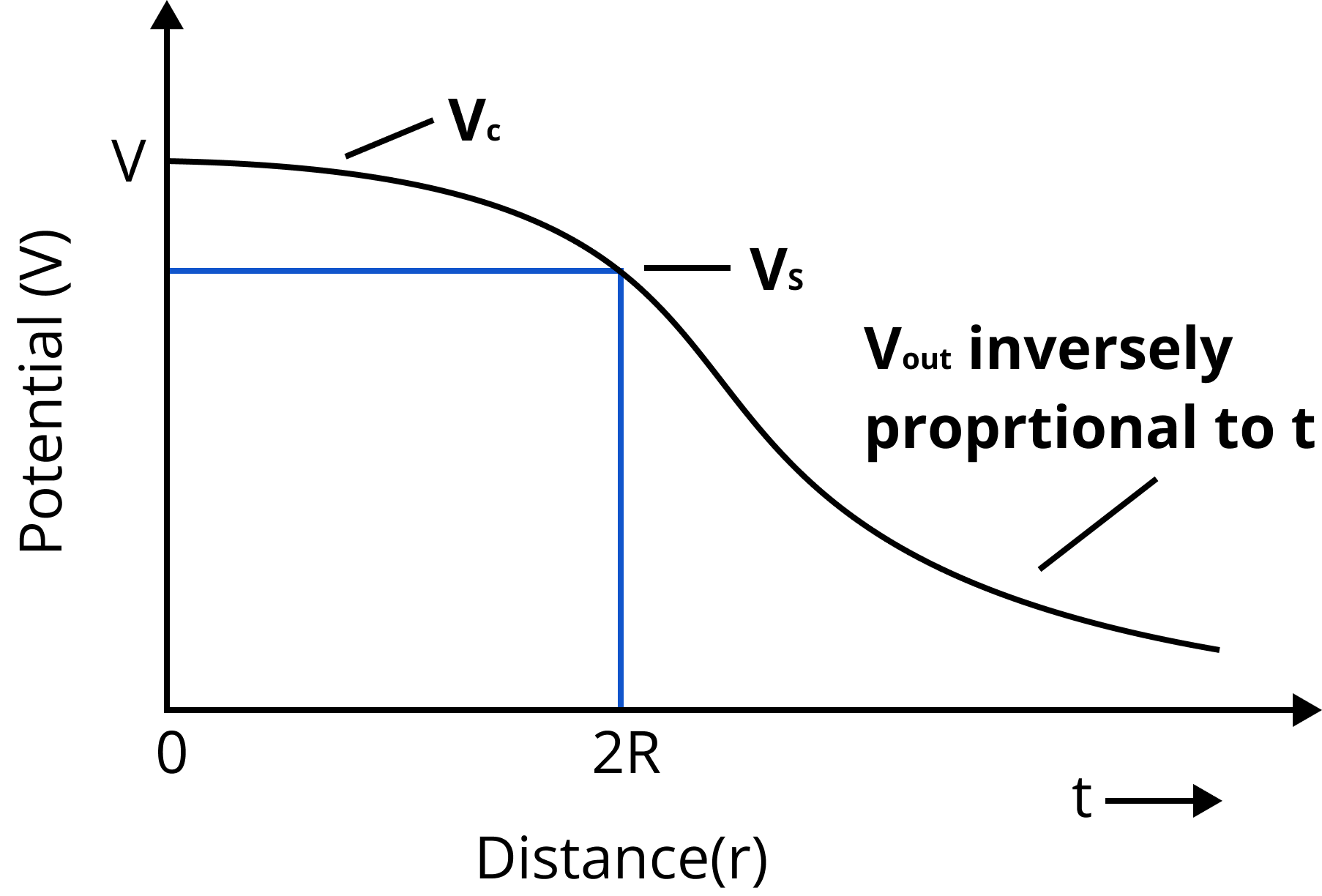
Variation of Potential and Radius for a Non-conducting Sphere

Equipotential Surfaces:

An equipotential surface is a surface with a constant value of potential at all points on the surface.

Electric field lines are always perpendicular in an equipotential surface.

Work done in moving an electric charge from one point to another on an equipotential surface is zero.

Two equipotential surfaces can never intersect one another.

Relationship between $\vec E$ and $\vec V$

$\vec E =  - \nabla V$

Where $\nabla V = \left( {\hat i\dfrac{\partial }{{\partial x}} + \hat j\dfrac{\partial }{{\partial y}} + \hat k\dfrac{\partial }{{\partial z}}} \right)$

-ve Sign shows that the direction of E is the direction of decreasing potential.

Electric Potential Energy:

Electric potential energy of a system of charges is the total amount of work done in bringing the various charges to their respective positions from infinitely large mutual separations.

The SI unit of electrical potential energy is joule.

Electric potential energy of a system of two charges is $U = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{{{q_1}{q_2}}}{{{r_{12}}}}$

Where ${r_{12}}$ is the distance between ${q_1}$ and ${q_2}$.

Electric potential energy of a system of n point charges 

$U = \dfrac{1}{{4\pi {\varepsilon _0}}}\sum\limits_{{\text{all pairs}}} {\dfrac{{{q_j}{q_k}}}{{{r_{jk}}}}} $

Note in this summation, we should include only one term for each pair of charges.

Conductors and Insulators

Those substances which can easily allow electricity to pass through them are called conductors. 

They have a large number of free-charge carriers that are free to move inside the material. Metals, human and animal bodies on earth are conductors. 

Those substances which do not allow electricity to pass through them are called insulators also called dielectrics.

Basic Electrostatics Properties of a Conductor:

Inside a conductor, the electric field is zero. 

At the surface of a charged conductor, the electric field must be normal to the surface at every point.

The interior of a conductor can have no excess charge in a static situation.

Electric potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface.

Electric field at the surface of a charged conductor

$\vec E = \dfrac{\sigma }{{{\varepsilon _0}}}\hat n$

Where $\sigma $ the surface is charge density and $\hat n$ is a unit vector normal to the surface in the outward direction.

Electrostatic Shielding: It is the phenomenon of protecting a certain region of space from the external electric field.

Dielectrics and Polarisation:

Dielectrics: Dielectrics are non-conducting substances. In contrast to conductors, they have no (or negligible number of) charge carriers.

Polar Molecule: A polar molecule is one in which the centres of positive and negative charges are separated (even when there is no external field). A polar molecule has a permanent dipole moment. Example: Water (${H_2}O$) and HCL.

The relationship between dielectrics and polarisation is given by $\vec{P}=\varepsilon_{o} \chi_{e} \vec{E}$ where $\vec{P}$ is polarisation, $\varepsilon_{o}$ is permittivity in free space, $\chi_{e}$ is called susceptibility of the dielectric medium which is equal to $\varepsilon_{r}-1$ where $\varepsilon_{r}$ is called dielectric constant and $\vec{E}$ is the electric field of the medium.

Non-polar Molecule: A nonpolar molecule is one in which the centres of positive and negative charges coincide. A nonpolar molecule has no permanent dipole moment. Example: Oxygen (${O_2}$ ) and Hydrogen (${H_2}$).

Polarisation: The dipole moment per unit volume is called polarisation and is denoted by P.

For, linear isotropic dielectrics $\overrightarrow P  = \chi \overrightarrow E $  where ${\chi _p}$  is a constant characteristic of the dielectric and is called the electric susceptibility of the dielectric medium.

Capacitance:

Capacitance (C) of a capacitor is the ratio of charge (Q) given and the potential (V) to which it is raised.

$C = \dfrac{Q}{V}$ 

The SI unit of capacitance is the farad (F).

1 millifarad(mF) = ${10^{ - 3}}$ farad

1 microfarad(Μf) = ${10^{ - 6}}$ farad

1 picofarad(pF) = ${10^{ - 12}}$ farad

Capacitance is a scalar quantity. The dimensional formula of capacitance is $\left[ {{M^{ - 1}}{L^{ - 2}}{T^4}{A^2}} \right]$ .

The Capacitance of Spherical Conductor:

Capacitance of a spherical conductor of radius R is $C = 4\pi {\varepsilon _0}R$. Taking earth to be a conducting sphere of radius 6400 km, its capacitance will be:

$C = 4\pi {\varepsilon _0}R = \dfrac{{6.4 \times {{10}^6}}}{{9 \times {{10}^9}}} = 711\mu F$ 

Capacitor:

A condenser or a capacitor is a device that stores electric charge. It consists of two conductors separated by an insulator or dielectric medium. The two conductors carry equal and opposite charges $\pm Q$ .

In an electrical circuit, a capacitor of fixed capacitance is represented but the symbol as shown in the figure:

Simple Capacitor

Variable Capacitor

Types of Capacitors:

Depending on their geometry, capacitors are classified as:

• Parallel plate capacitor

• Cylindrical capacitor

• Spherical capacitor

Parallel Plate Capacitor: It consists of two similar flat conducting plates, arranged parallel to one another, separated by a distance. Its capacitance is given by

$C = \dfrac{{{\varepsilon _0}A}}{d}$ (When air is between the plates)

$C = \dfrac{{K{\varepsilon _0}A}}{d}$ (When dielectric is between the plates)

Where A is the area of each plate and d is separation between the two plates.

When a dielectric slab of thickness t and dielectric constant K is introduced between the plates, then the capacitance of a parallel plate capacitor is given by

$C = \dfrac{{{\varepsilon _0}A}}{{d - t\left( {1 - \dfrac{1}{K}} \right)}}$ 

When a metallic conductor of thickness t is introduced between the plates, then capacitance of a parallel plate capacitor is given by: 

$C = \dfrac{{{\varepsilon _o}A}}{{d - t}}$ 

Cylindrical capacitor: It consists of two coaxial cylinders of same length.

Capacitance of an air filled cylindrical capacitor is

$C = \dfrac{{2\pi {\varepsilon _0}L}}{{\ln \left( {\dfrac{b}{a}} \right)}}$ 

Where a, b are the inner and outer radii and L is the length.

Spherical Capacitor: It consists of two concentric spherical shells.

Capacitance of an air filled spherical capacitor is

$C = 4\pi {\varepsilon _0}\dfrac{{ab}}{{b - a}}$ 

Where a, b are the inner and outer radii.

Grouping of Capacitors:

Capacitors in Series: For n capacitors connected in series, the equivalent capacitance ${C_s}$  is given by:

$\dfrac{1}{{{C_s}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ..... + \dfrac{1}{{{C_n}}}$ 

Capacitors in parallel: For n capacitors connected in parallel, the equivalent capacitance ${C_p}$  is given by

${C_p} = {C_1} + {C_2} + ..... + {C_n}$

When capacitors are connected in series, the charge through each capacitor is the same.

When capacitors are connected in parallel, the potential difference across each capacitor is the same.

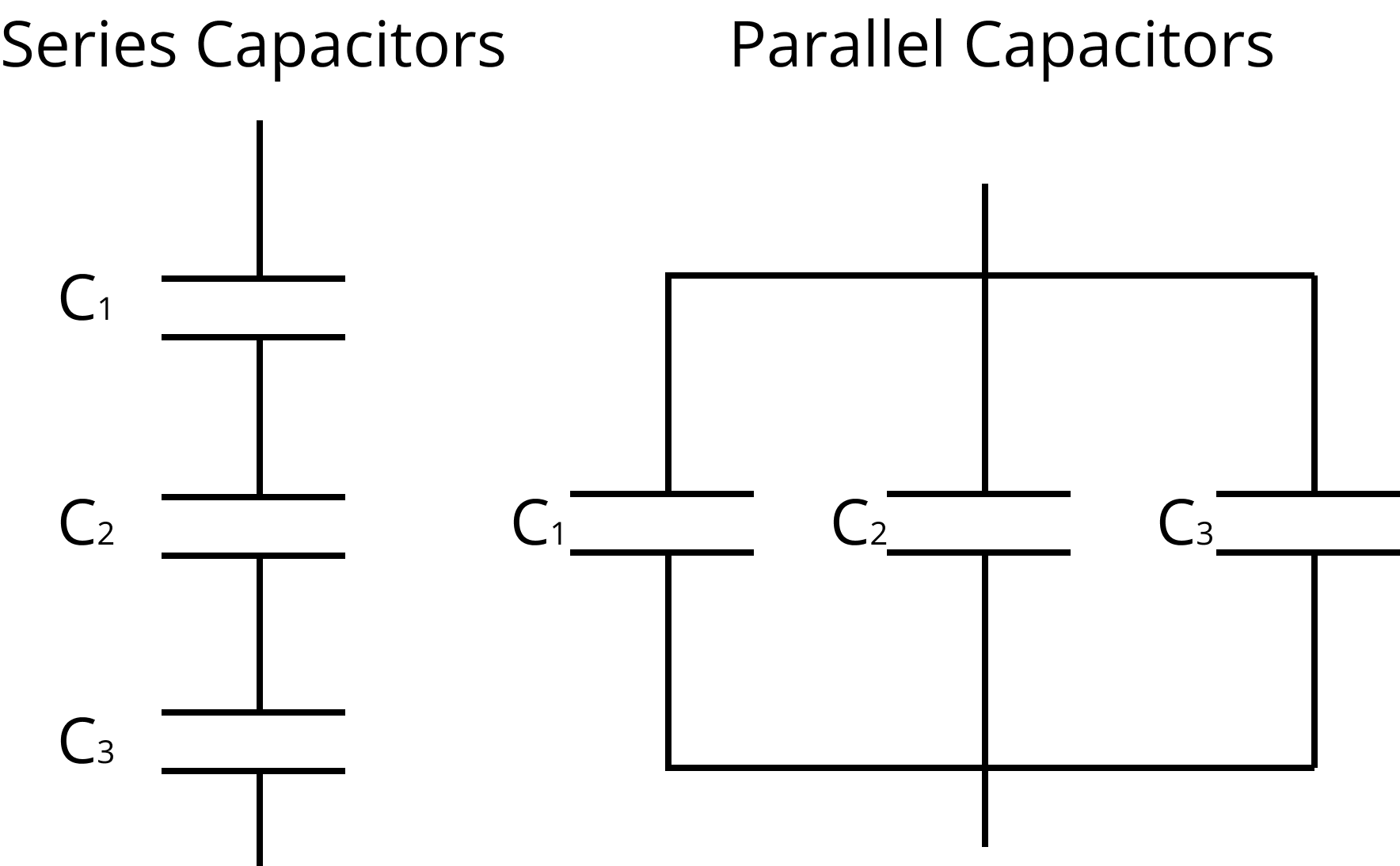
Series and Parallel Circuit

Energy Stored In a Capacitor:

Work done in charging a capacitor gets stored in the capacitor in the form of its electric potential energy and it is given by $U = \dfrac{1}{2}C{V^2} = \dfrac{1}{2}QV = \dfrac{1}{2}\dfrac{{{Q^2}}}{C}$ 

Energy Density:

The energy stored per unit volume in the electric field between the plates is called energy density (u).It is given by: 

$u = \dfrac{1}{2}{\varepsilon _0}{E^2}$

Sharing of Charges:

When two capacitors charged to different potentials are connected by a conducting wire, charge flows from the one at higher potential to the other at lower potential till their potentials become equal. The equal potential is called common potential. It is given by

$V = \dfrac{{{\text{Total charge}}}}{{{\text{Total capacity}}}} = \dfrac{{{Q_1} + {Q_2}}}{{{C_1} + {C_2}}} = \dfrac{{{C_1}{V_1} + {C_2}{V_2}}}{{{C_1} + {C_2}}}$ 

In sharing charges there is absolutely no loss of charge some energy is however, lost in the process in the form of heat etc which is given by ${U_1} - {U_2} = \dfrac{{{C_1}{C_2}{{({V_1} - {V_2})}^2}}}{{2({C_1} + {C_2})}}$

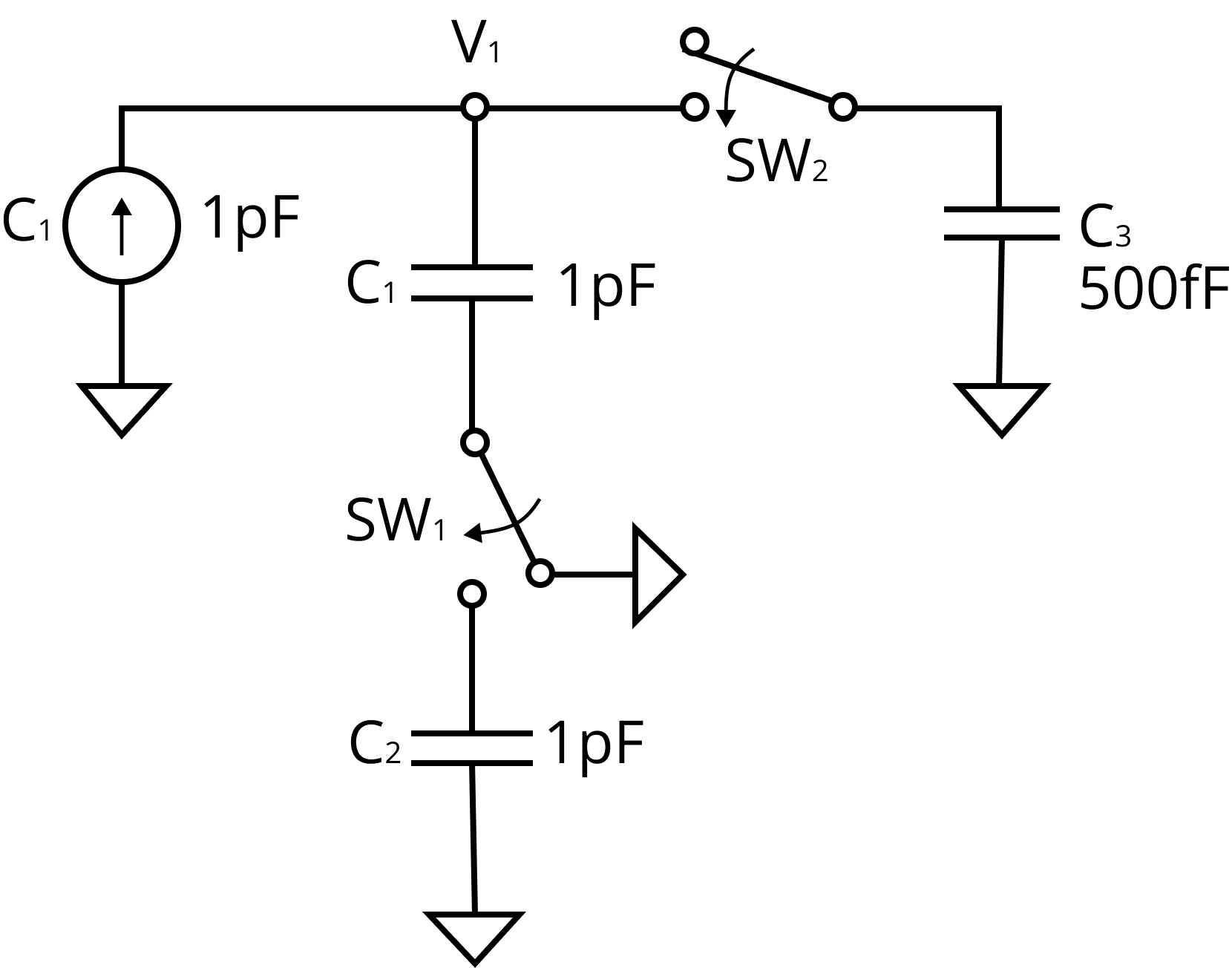
Sharing of charges in a capacitor

Effect of Dielectric:

When a dielectric slab of dielectric constant K is introduced between the plates of a charged parallel plate capacitor and the charging battery remains connected, then:

Potential difference between the plates remains constant  i.e.,  $V = {V_0}$

Capacitance increases  i.e., $C = K{C_0}$

Charge on a capacitor increases  i.e.,  $Q = K{Q_0}$

Electric field between the plates remains unchanged  i.e.,  $E = {E_0}$

Energy stored in a capacitor increases  i.e., $U = K{U_0}$

When a dielectric slab of dielectric constant K is introduced between the plates of a charged parallel plate capacitor and the charging battery is disconnected, then

Charge remains unchanged  i.e.,   $Q = {Q_0}$

Capacitance increases   i.e.,  $C = K{C_0}$

Potential difference between the plates decreases  i.e.,  $V = \dfrac{{{V_0}}}{K}$

Electric field between the plates decreases  i.e.,  $E = \dfrac{{{E_0}}}{K}$

Energy stored in the capacitor decreases  i.e.,  $U = \dfrac{{{U_0}}}{K}$

Where ${Q_0},{C_0},{V_0},{E_0}$ and ${U_0}$ represents the charge, capacitance, potential difference, electric field and energy stored in the capacitor of a charged air filled parallel plate capacitor.

Van De Graaff Generator:

A Vande Graaff generator consists of a large spherical conducting shell (a few metres in diameter).By means of a moving belt and suitable brushes, charge is continuously transferred to the shell and potential difference of the order of several million volts is built up which can be used for accelerating charged particles.

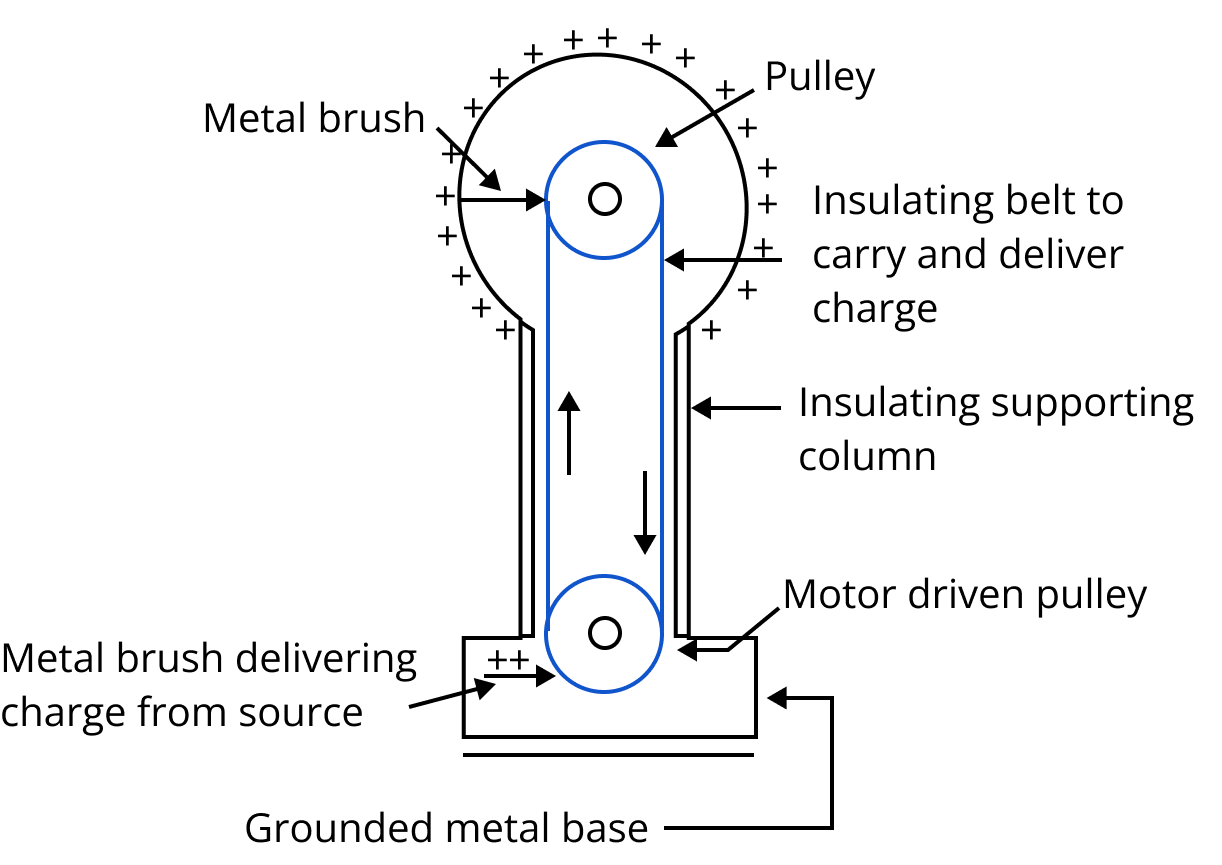
Parts of Van De Graff Generator

Points to Remember:

Electrostatic potential at a point can be physically interpreted as the work done by the field in displacing a unit positive charge from some reference point to the given point.

Potential difference is defined as the amount of work done in moving a unit positive charge from one point to another point.

Potential can be expressed and defined for a dipole, point charge and a system of charges, for uniformly spherical conducting and non-conducting shells.

An equipotential surface is a surface with a constant value of potential at all points on the surface. Work done in moving an electric charge from one point to another on an equipotential surface is zero.

Relationship between $\vec E$ and $\vec V$ $\vec E =  - \nabla V$

Electric potential energy of a system of charges is the total amount of work done in bringing the various charges to their respective positions from infinitely large mutual separations.

Those substances which can easily allow electricity to pass through them are called conductors. They have a large number of free-charge carriers that are free to move inside the material. Metals, human and animal bodies on earth are conductors. 

Those substances which do not allow electricity to pass through them are called insulators also called dielectrics.

• Electrostatic shielding: It is the phenomenon of protecting a certain region of space from the external electric field.

• Dielectrics: Dielectrics are non-conducting substances. In contrast to conductors, they have no (or negligible number of) charge carriers.

• Polar molecule: A polar molecule is one in which the centres of positive and negative charges are separated (even when there is no external field). A polar molecule has a permanent dipole moment. Example: Water (${H_2}O$) and HCL.

• Non-polar molecule: A nonpolar molecule is one in which the centres of positive and negative charges coincide. A nonpolar molecule has no permanent dipole moment. Example: Oxygen (${O_2}$ ) and Hydrogen (${H_2}$).

• Polarisation: The dipole moment per unit volume is called polarisation and is denoted by P.

Capacitance (C) of a capacitor is the ratio of charge (Q) given and the potential (V) to which it is raised.

A condenser or a capacitor is a device that stores electric charge. It consists of two conductors separated by an insulator or dielectric medium.

Types of capacitor are parallel, cylindrical, spherical capacitors.

Capacitors can be grouped either in series or in parallel in the circuit.

Work done in charging a capacitor gets stored in the capacitor in the form of its electric potential energy and it is given by $U = \dfrac{1}{2}C{V^2} = \dfrac{1}{2}QV = \dfrac{1}{2}\dfrac{{{Q^2}}}{C}$ 

The energy stored per unit volume in the electric field between the plates is called energy density (u).

Sharing of charges and effect of dielectric on capacitance

A Vande Graaff generator consists of a large spherical conducting shell (a few metres in diameter).By means of a moving belt and suitable brushes, charge is continuously transferred to the shell and potential difference of the order of several million volts is built up which can be used for accelerating charged particles.

Important Formulae:

$V = \dfrac{W}{{{q_0}}}$

$\vec E =  - gradV =  - \vec \nabla V =  - \dfrac{{\partial V}}{{\partial x}}\hat i - \dfrac{{\partial V}}{{\partial y}}\hat j - \dfrac{{\partial V}}{{\partial z}}\hat k$

${V_{ab}} =  - \int\limits_a^b {\vec E.d\vec r} $

$V = \dfrac{q}{{4\pi {\varepsilon _0}r}}$ (for a point charge)

$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{{q_1}}}{{{r_1}}} + \dfrac{{{q_2}}}{{{r_2}}} + \dfrac{{{q_3}}}{{{r_3}}} + ......\dfrac{{{q_n}}}{{{r_n}}}} \right) = \dfrac{1}{{4\pi {\varepsilon _0}}}\sum\limits_{i = 1}^n {\dfrac{{{q_i}}}{{{r_i}}}}$ (for a system of charges)

$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{p\cos \theta }}{{{r^2}}}$

Electric potential due to uniformly charged thin spherical shell:

$V = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{r}$ (Outside the shell)

$V = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{R}$ (At the surface)

$V = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{R}$ (Inside the shell)

Here, $q = 4\pi {R^2}\sigma $

Electric potential due to a uniformly charged non conducting solid sphere:

$V = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{r}$ (Outside)

$V = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{q}{R}$ (At the surface)

$V = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{{q\left( {3{R^2} - {r^2}} \right)}}{{2{R^3}}}$ (Inside)

Here $q = \dfrac{4}{3}\pi {R^2}\rho $

Relationship between $\vec E$ and $\vec V$

$\vec E =  - \grad Vv$

Where $\grad V = \left( {\hat i\dfrac{\partial }{{\partial x}} + \hat j\dfrac{\partial }{{\partial y}} + \hat k\dfrac{\partial }{{\partial z}}} \right)$

$U = \dfrac{1}{{4\pi {\varepsilon _0}^{}}}\dfrac{{{q_1}{q_2}}}{{{r_{12}}}}$

$U = \dfrac{1}{{4\pi {\varepsilon _0}}}\sum\limits_{{\text{all pairs}}} {\dfrac{{{q_j}{q_k}}}{{{r_{jk}}}}} $

$C = \dfrac{{{\varepsilon _0}A}}{d}$ (When air is between the plates)

$C = \dfrac{{K{\varepsilon _0}A}}{d}$ (When dielectric is between the plates)

$C = \dfrac{{2\pi {\varepsilon _0}L}}{{\ln \left( {\dfrac{b}{a}} \right)}}$ (for cylindrical capacitors)

$C = 4\pi {\varepsilon _0}\dfrac{{ab}}{{b - a}}$ (for spherical capacitors)

Capacitors in series: For n capacitors connected in series, the equivalent capacitance ${C_s}$  is given by:

$\dfrac{1}{{{C_s}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ..... + \dfrac{1}{{{C_n}}}$ 

Capacitors in parallel: For n capacitors connected in parallel, the equivalent capacitance ${C_p}$  is given by

${C_p} = {C_1} + {C_2} + ..... + {C_n}$

Energy stored in a capacitor: $U = \dfrac{1}{2}C{V^2} = \dfrac{1}{2}QV = \dfrac{1}{2}\dfrac{{{Q^2}}}{C}$ 

Energy density: $u = \dfrac{1}{2}{\varepsilon _0}{E^2}$

Sharing of charges: $V = \dfrac{{{\text{Total charge}}}}{{{\text{Total capacity}}}} = \dfrac{{{Q_1} + {Q_2}}}{{{C_1} + {C_2}}} = \dfrac{{{C_1}{V_1} + {C_2}{V_2}}}{{{C_1} + {C_2}}}$ 

Questions:

1) Two Capacitors are charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of resulting system is:

a) Decreases by a factor of 2

b) Remains the same

c) Increases by a factor of 2

d) Increases by a factor of 4

Answer: option a)

Solution:

When a capacitor is charged by a battery of potential v, the energy stored in the capacitor is $U = \dfrac{1}{2}C{V^2}$ .

When a battery is removed another identical uncharged capacitor is connected in parallel then common potential would be:

${V^1} = \dfrac{{CV}}{{C + C}} = \dfrac{V}{2}$ 

$\therefore $ Then the energy stored in the capacitor,

${U_f} = \dfrac{1}{2}(2C)\left( {\dfrac{V}{2}} \right) = \dfrac{1}{4}C{V^2}$ 

$\therefore $ From eqns. (i) and (ii)

${U_f} = \dfrac{{{U_i}}}{2}$  .

Thus the energy is reduced by the factor of 2 and option (a) is correct.

2) The electric potential V at any point x, y, z (all in metres) is given by $V = 4{x^2}$ V. Then which of the following statements is true about its potential?

a) Potential at y and z is 0.

b) Potential at point (1, 0, 2) has magnitude of 8

c) Potential at point (1, 0, 2) is $ - 8\widehat i$ $V{m^{ - 1}}$ 

d) All of them are true

Answer: Option a), b) and c) 

Solution:

Given: $V = 4{x^2}$ 

${E_x} =  - \dfrac{{\delta V}}{{\delta x}} =  - \dfrac{{\delta (4{x^2})}}{{\delta x}} =  - 8x$ 

Here as V is depending only on x its potential on y and z is always 0.

At x=1m, potential is:

$\overrightarrow V  =  - 8x =  - 8\widehat i$ $V{m^{ - 1}}$ 

Its magnitude would be $V = \sqrt {{{( - 8)}^2}}  = 8$ 

Thus, options a), b) and c) are true.       

Importance of Class 12 Physics NEET Electrostatic Potential and Capacitance

The chapter on Electrostatic Potential and Capacitance will define what an electric charge is along with the difference between positive and negative charges. Students will learn how to compare mass and charge and their properties to understand the core concepts of this chapter.

The chapter will also introduce new concepts related to point charge, dimensional formula, unit formula, and different methods of charging. Students will also find out what an electroscope is and its implications in the modern world.

The laws related to electricity will be explained using various mathematical tools and scientific derivations. Students will understand how these laws define something universal and can use them to solve fundamental problems in the NEET exam.

They will learn what an electric field is and how its intensity can be defined using various laws and fundamental principles. This chapter is very important as it builds a strong foundation of the concepts of electricity, electric charge, electric potential and capacitance. Comprehending these new concepts becomes a lot easier when you use Electrostatic Potential and Capacitance NEET notes.

Benefits of Vedantu’s Electrostatic Potential and Capacitance NEET Notes

These notes have been compiled by the experts by focusing on the objectives of scientific principles related to static electricity, electrostatic potential, and capacitance. You will find these simpler explanations of this chapter very useful to study and complete preparing this chapter.

The concepts related to electric charge, field intensity of electricity, electric field lines, and the motion of charged particles will be simplified for better comprehension. You will become skilled at using the scientific derivation and formulae of this chapter to solve conceptual NEET questions easily.

Use these notes to revise this chapter within a short span of time and prepare a stronghold on the concepts. Learn how the experts have explained them simply to grab the principles and their objectives faster.

Revise using these notes and save your precious time. Recall the laws, definitions, meaning, scientific derivations, etc. in no time by referring to these Electrostatic Potential and Capacitance NEET notes and become better at answering fundamental questions.

Download Electrostatic Potential and Capacitance Notes PDF

There is no need to worry about preparing concise notes on your own when you can easily download the PDF version of Electrostatic Potential and Capacitance revision notes. Get the best guidance and revision help from these notes and make your study sessions more productive. Master the techniques used by the experts to solve sample questions and score well in the NEET exam.

NEET Physics Revision Notes - Chapter Pages

Other Important Links