Work, Energy and Power: An Important Concept for NEET
This chapter of work, energy and power deals with the prior revision of all the concepts we studied in our lower grades to build the connection between the advanced parts of the same. In work, energy and power, we have already studied the formulae which describe physical entities like energy, force and work creating the basics of other derived quantities.
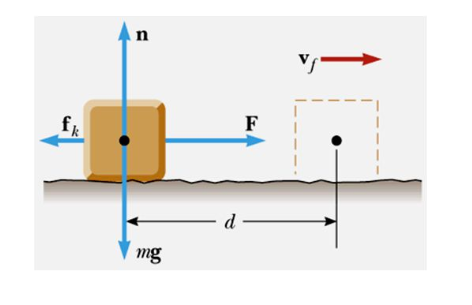
In Physics, work is defined as the scalar product of force and displacement which sometimes is also considered as the work done by a constant force.
W =
Or W=Fs
Here F is the force and s is the displacement whereas theta is the angle acting between both of them. This relation helps to understand the various related terms like the angle between force and displacement, and what is the nature of work associated with these two quantities.
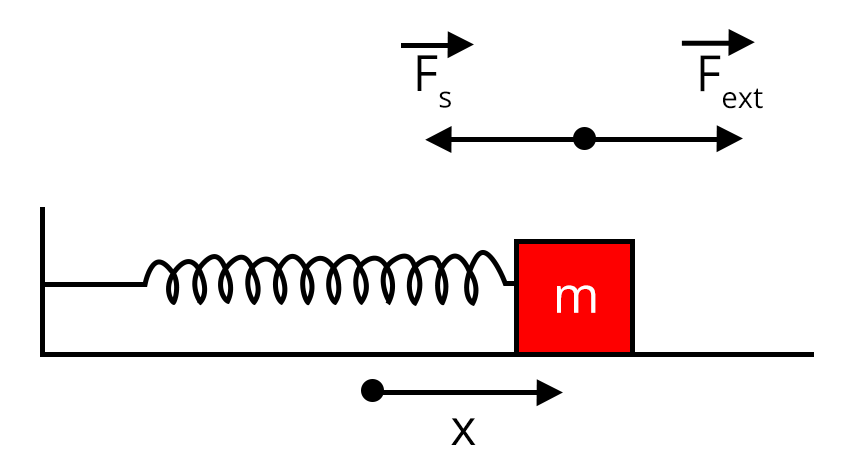
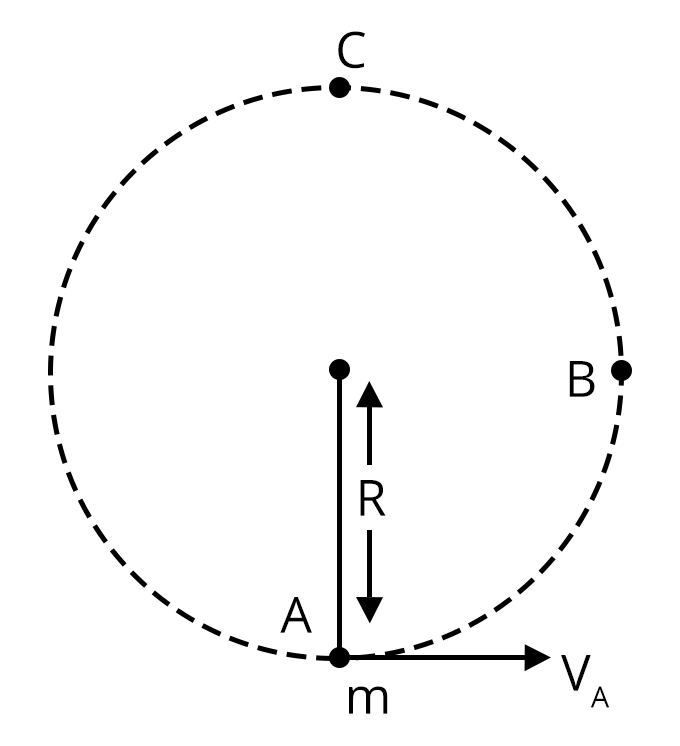
Moving further, the chapter brings into light the concepts of work done by variable force, the Work-Energy theorem and some other forms of energy. We have also studied the conservative and non-conservative forces and the stability of equilibrium when different forces act in the system, Gravitational Potential energy motion in the vertical circle, energy related to the spring system, etc.
Now, let us move on to the important concepts and formulae related to NEET exams along with a few solved examples.
Important Topics of Work, Energy and Power
Work and its unit
Work done by a Variable force
Work Energy Theorem
Conservative Forces
The potential energy of spring
Gravitational Potential Energy
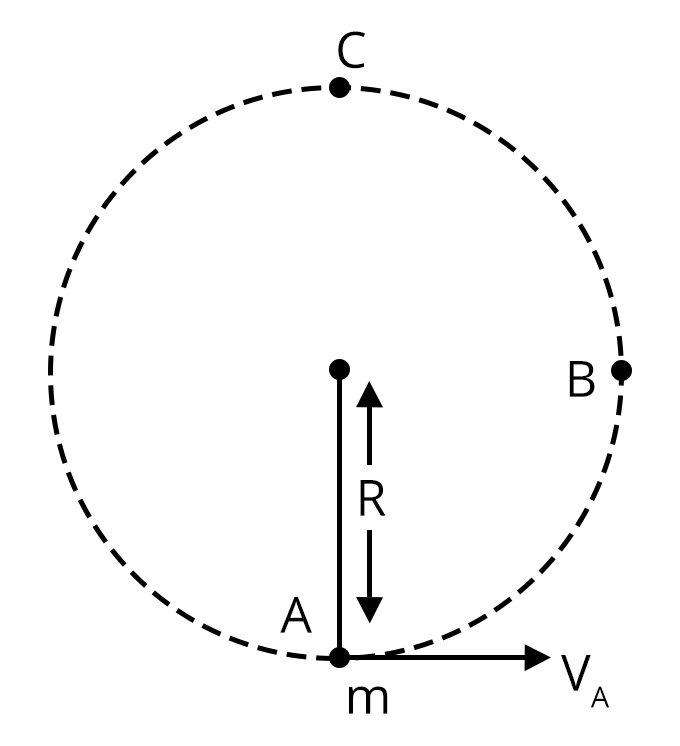
Vertical Circular Motion
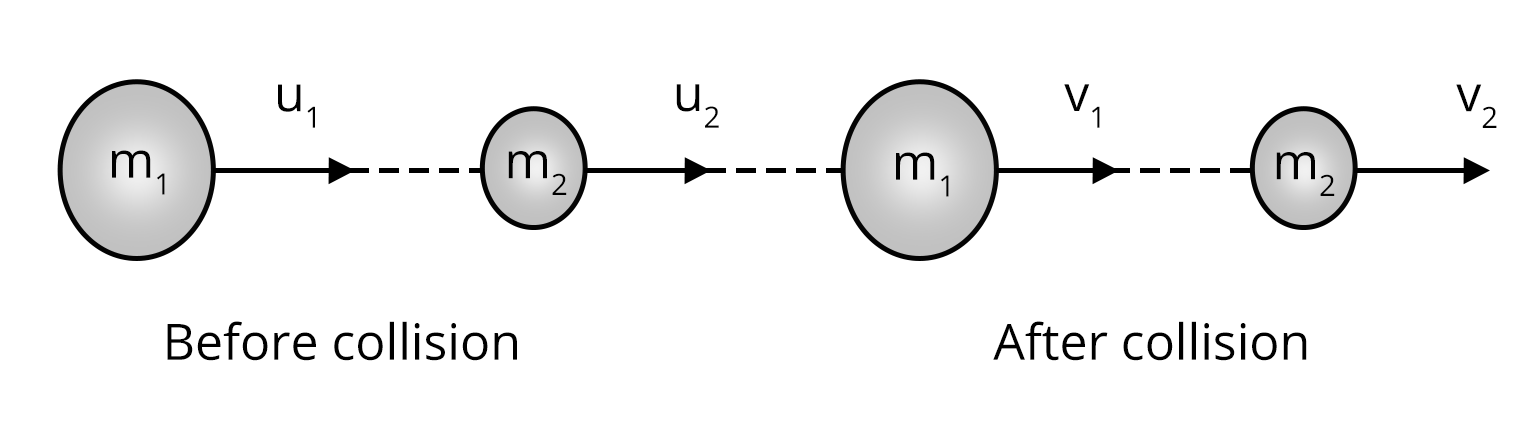
Elastic Collision
Inelastic Collision
Energy and its various types
Conservation of Mechanical Energy
Energy and its various types
Important Concepts of Work, Energy and Power
List of Important Formulae
Solved Examples from Work, Energy and Power
1. A porter lifts a suitcase weighing 20kg from the platform and carries it in his hand 2.0m above the platform. Calculate the work done by the porter on the suitcase.
Sol:
Given,
Hence
Key Point: Here, only the work done against gravity will act since the kinetic energy of the suitcase is zero.
2. An elevator weighing 500kg is to be lifted up at a constant velocity of 0.20m/s. What would be the minimum horsepower of the motor to be used?
Sol:
Given, m = 500kg, Velocity = 0.20/s
g= 10 m/s2
We have to calculate the power in horsepower.
We know
Where F is force acting on the elevator. Thus,
Hence,
=(500)(0.20)(10)
=1000W
And
Therefore, Power in hp = 1000/760 = 1.315hp
Key Point: Here only power’s formula is the main thing that students should remember.
Previous Year Questions from NEET Paper
1. A force F = 20+10y acts on a particle in y direction where F is in newton and y in metres. The work done by this force to move the particle from y=0 to y=1m is (NEET 2019)
Sol:
Given, F = (20+10y) N
We have to calculate the work done from y=0 to y=1m.
Here, the force acting is variable force; hence
W=
=
=
=25J
Hence, the work done by this force to move the particle from y=0 to y=1m is 25 J.
Trick: We can solve the question using the formula of power.
2. The work done to raise a mass m from the surface of the earth to a height h, which is equal to the radius of the earth, is: (NEET 2019)
Sol:
The initial potential energy of the mass at the surface of the earth having radius R is
Ui =
When mass m is raised to height h, the final energy becomes
Uf =
Hence, the work done here will be the change in kinetic energy = Uf-Ui
=
=
=
But g=
Hence, the final work done is
Trick: We can solve the question with the help of the work-energy theorem.
Practice Questions
1. A cyclist comes to a skidding stop at 10m. During this process, the force on the cycle due to the road is 200N and is directly opposed to the motion. How much work does the road do on the cycle?
Ans -2000J
2. A ball with a velocity of 5 m/s impinges at an angle of 60˚ with the vertical on a smooth horizontal plane. If the coefficient of restitution is 0.5, find the velocity and direction after the impact.
Ans: v = 0.3m/s and the direction will be perpendicular to the surface
Conclusion
In this article, we have provided all important information regarding the chapter Work, Energy and Power. Some of these include important formulae, concepts, etc. Students should work on more solved examples, sample papers and previous year questions for securing good marks in the NEET exam.
NEET Important Chapter - Work, Energy and Power

 Share
ShareFAQs on NEET Important Chapter - Work, Energy and Power
1. What is the weightage of the Work, Energy and Power in NEET?
Nearly 2-3 questions appear in the exam from this chapter covering about 10 marks which makes about 2% of the total marks.
2. What are the key points that need to be practised for solving questions from Work, Energy and Power?
Students should practice the work-energy theorem and vertical circular motion for solving the questions from the Work, Energy and Power.
3. Are previous year's questions enough for NEET?
To score 600+ in NEET, NCERT (both 11th and 12th) and previous year NEET papers are sufficient. Solving the previous 10 years' question papers for NEET examinations offers a tremendous advantage because 2-3 questions with identical alternatives are guaranteed to be repeated every year.








 Watch Video
Watch Video