Magnification Formula for Mirror

Magnification is the term used to describe the increase in picture size caused by spherical mirrors that are concave or convex in relation to the size of the item. It is represented by the symbol m and is thought to be the height-to-object height ratio.

Some optical devices help with vision by enlarging small or far-off objects:

• A magnifying glass that allows the user to hold objects closer to their eyes while using a positive (convex) lens to make objects appear larger.

• A telescope that makes an image of a faraway object using its huge objective lens or primary mirror and then enables the user to closely inspect the image using a smaller eyepiece lens, making the item appear larger.

• A microscope, which at a comfortable viewing distance magnifies a small item into a much bigger image.

The magnification created by a spherical mirror, which is symbolized by the letter "m," can be expressed or represented as follows:

Consequently, \[{\rm{m = }}\dfrac{h}{{h'}}\]

where h' denotes the height of the object and h represents the height of the image.

Mirror and Magnification Formula

Magnification can be characterized as how much the image enlarges or reduces in size in relation to the object size. It is shown as the height of the image divided by the height of the object. The letter "m" stands for magnification. Where,

Magnification \[{\rm{(m) = }}\dfrac{h}{{h'}}\]

And h is the object height, while h' is the image height.

Because magnification is also influenced by object and image distance, it can alternatively be written as:

\[{\rm{m = }}\dfrac{{ - v}}{u}\]

where the object distance is u and the picture distance is v.

As a result, the expression for magnification mirror is:

\[m = \dfrac{h}{{h'}} = \dfrac{{ - v}}{u}\]

Sign Convention Chart for Reference

The "New Cartesian Sign Convention" is a set of guidelines that the sign convention for spherical mirrors abides with, as stated below:

• The origin is represented by the mirror's pole (p) as shown in the Figure below.

• The coordinate system's x-axis is represented by the principal axis.

• The item is kept to the left of the mirror. This must always be adhered to.

• From the pole (p), the distances parallel to the principal axis must be calculated.

• All distances measured from the pole (p) on the right side of the mirror are assumed to be positive, while those on the left side of the mirror are assumed to be negative.

• Positive distances are those that are perpendicular to and above the principal axis.

• All distances below the principal axis must be interpreted as negative.

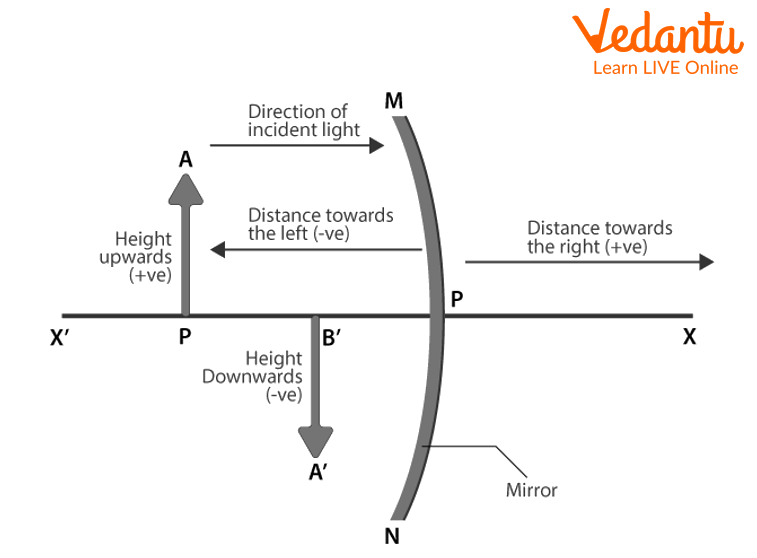
Sign Convention Chart

Unit of Magnifying Power

The ratio of the image distance to the object distance and the ratio of the image height to the object height are used in both instances to calculate magnification. Because of this, magnification lacks dimensions. It is a parameter without dimensions and without units.

Uses of Magnification

• A precision magnifier serves the same purpose as a very basic magnification, but it contains additional components that help to remove aberrations and provide crisper images for our eyes.

• A tiny water droplet serves as a crude magnifier, enlarging the object behind it. The impact of surface tension causes the water to condense into tiny, sphere-shaped droplets. A spherical shape is distorted but still able to create a good image of the object when the water droplet comes into contact with it.

Solved Problems

1. If the image distance is 6 cm and the object is at a distance of 12 cm in the case of a concave mirror, what is the magnification formula for concave mirror produced?

Ans: To determine magnification,

\[{\rm{m = }}\dfrac{{ - v}}{u}\]

The signs are supplied using sign convention with v= -6 cm and u= -12 cm as the specified values.

\[{\rm{m = }}\dfrac{{ - ( - 6)}}{{ - 12}}\]

$\therefore m = -0.5$

As a result, there is a 0.5-factor drop.

2. Amit maintained a pencil parallel to the main axis of a concave mirror directly in front of it. The focal length of the mirror is 30 cm. Two times the size of a pencil, the image is created. Determine the distance between the object and the mirror.

Ans: Magnification \[m = \dfrac{h}{{h'}} = \dfrac{{ - v}}{u}\]

For real image:

\[m = \dfrac{{ - v}}{u} = - 2\]

$\Rightarrow v= 2u$

By means of the mirror equation,

\[\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}\]

\[\Rightarrow \dfrac{1}{{2u}} + \dfrac{1}{u} = \dfrac{1}{{ - 30}}\]

$\therefore u=-45\,cm$

This sits in the middle of the Curvature and the Focal Length.

For virtual images:

\[m = \dfrac{{ - v}}{u} = 2\]

v= -2u

By means of the mirror equation,

\[\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}\]

\[\Rightarrow \dfrac{1}{{ - 2u}} + \dfrac{1}{u} = \dfrac{1}{{ - 30}}\]

$\therefore u=-15\,cm$

Conclusion

The following should be kept in mind while determining the magnification for spherical mirrors:

• A virtual and upright image indicated by the magnification's positive value.

• A real and inverted image indicated by the negative value of the magnification.

• The object distance (u) and focal length (f) for a concave mirror are both negative according to the sign conventions.

• The image distance (v), according to the sign conventions, is positive for a virtual image and negative for a real image.