Question

(0, -1), (0, 3) are the two opposite vertices of a square. Find the coordinates of the other two vertices.
(a)(0, 1), (0, -3)
(b)(3, -1), (0, 0)
(c)(2, 1), (-2, 1)
(d)(2, 2), (1, 1)

Answer 1

Hint: Use the condition that all side lengths in a square are equal.
Apply distance formula,
\[\text{distance between }\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)\text{ =}\sqrt{{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}}\]

By equating the distances, find the coordinates of both the remaining vertices.

Complete step-by-step answer:

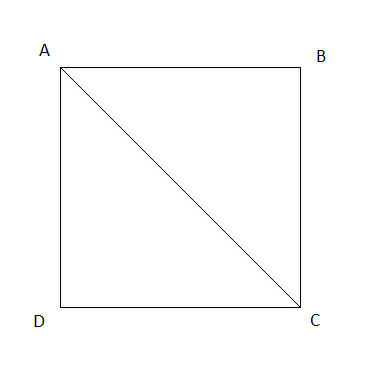
Let the given vertices be A(0, -1), C(0, 3) of the square ABCD. Let us assume the vertex B to be (x, y).
By applying all the sides are equal condition, we get:
AB = CB = a…..(1)
By applying distance formula,
\[\text{Distance between }\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)\text{ =}\sqrt{{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}}\]
Distance between A and B = AB
\[AB=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( y-\left( -1 \right) \right)}^{2}}}=\sqrt{{{x}^{2}}+{{\left( y+1 \right)}^{2}}}.....(2)\]
Distance between C and B = CB
\[CB=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}=\sqrt{{{x}^{2}}+{{\left( y-3 \right)}^{2}}}.....(3)\]
By substituting equation (2) and equation (3) in equation (1), we get:
\[\sqrt{{{x}^{2}}+{{\left( y+1 \right)}^{2}}}=\sqrt{{{x}^{2}}+{{\left( y-3 \right)}^{2}}}\]
By squaring on both sides, we get:
\[{{x}^{2}}+{{\left( y+1 \right)}^{2}}={{x}^{2}}+{{\left( y-3 \right)}^{2}}\]
By cancelling common terms and expanding equation, we get:
\[{{y}^{2}}+2y+1={{y}^{2}}-6y+9\]
By sending all terms to one side and simplifying, we get:
\[\begin{align}
  & 8y=8 \\
 & y=1 \\
\end{align}\]
As you can see in the figure ABC form right angle triangle,
By applying Pythagoras Theorem,
\[A{{B}^{2}}+C{{B}^{2}}=A{{C}^{2}}.....\left( 4 \right)\]
By equation (2) and equation (3), we get AB and CB.
Distance between A and C = AC
\[AC=\sqrt{{{\left( 0-0 \right)}^{2}}+{{\left( 3+1 \right)}^{2}}}=\sqrt{16}=4.....\left( 5 \right)\]
By substituting equation (5), equation (2) and equation (3) in equation (4) we get:
\[{{x}^{2}}+{{\left( y+1 \right)}^{2}}+{{x}^{2}}+{{\left( y-3 \right)}^{2}}={{4}^{2}}=16\]
By solving and substituting y=1 into the above equation, we get:
\[2{{x}^{2}}+{{2}^{2}}+{{\left( -2 \right)}^{2}}=16\]
By simplifying, we get:
\[\begin{align}
  & 2{{x}^{2}}=16-8=8 \\
 & {{x}^{2}}=4 \\
\end{align}\]
After applying root we need to consider the negative value also,
By applying square root on both sides, we get:
\[x=\sqrt{4}=2\text{ or -2}\].
We know y = 1.
By above 2 equations, we get two points, which are (2, 1), (-2, 1).
These two points are the vertices B and D.
\[\therefore \]The remaining two opposite vertices are (2, 1), (-2, 1).
So option (c) is the correct answer.

Note: While applying distance formula be careful with coordinates. Don’t mix up or else you may reach the wrong answer.
Don’t forget to consider the negative root while applying the square root of the number.
If you don’t consider the negative root, you get only one point but we need the remaining two points. So, for that second point we need the negative root.