Question

How many 3 m cubes can be cut from a cuboid measuring $18m\,\times 12m \, \times\,9 m$?

Answer 1

Hint: Here, first find the volume of cuboid then volume of cube. Assume there are n cubes, and equate the volumes of cube and cuboid. And by solving the equation, find the number of cubes.

Complete step by step answer:
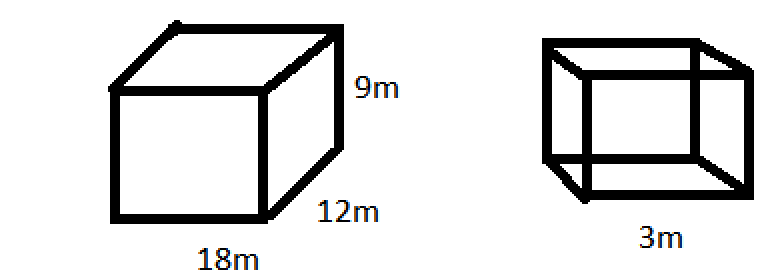
Given, the measurement of the cuboid is 18 m by 12 m by 9 m.
Volume of cuboid = Length × Breadth × Height
Here, Length = 18 m, Breadth = 12 m, Height = 9 m
Volume of cuboid = 18 m × 12 m × 9 m = 1944 $m^3$
Also given, the side of the cube is 3 m.
Volume of cube = $\text{side}^3$
Volume of cube =$3m^3 = 27 m^3$
Let n be the number of cubes that can be cut from a cuboid measuring 18 m by 12 m by 9 m.
The volume of $n$ cubes of side 3 m $= 27n m^3$
In the conversion of shapes, volume remains the same.
Therefore, $27n = 1944$
$\Rightarrow n = \dfrac{{1944}}{{27}} = 72$

The number of cubes is 72.

Note:
In these types of questions, always use the concept that in the conversion of shapes volumes remains the same. For these types of questions to solve you must have volumes of some basic shapes.
The volume of cuboid = Length × Breadth × Height
The volume of cube = Side × Side × Side
The volume of the cylinder = $\pi {r^2}h$, where r is the radius and h be the height of the cylinder.
The volume of cone = $\dfrac{1}{3}\pi {r^2}h$, where r is the radius and h be the height of the cylinder.
Volume of sphere = $\dfrac{4}{3}\pi {r^3}$, where r is the radius of the sphere.
Volume of hemisphere = $\dfrac{2}{3}\pi {r^3}$, where r is the radius of hemisphere.