Question

A 1.5 meter tall boy saw the top of a building under construction at an elevation of \[30^\circ \]. The completed building was 10 meters higher and the boy saw its top at an elevation of \[60^\circ \] from the same spot. What is the height of the building?

Answer 1

Hint: Use trigonometry ratio \[\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}\] in the triangle making \[30^\circ \] and find the base from this then use this trigonometry ratio in the triangle making \[60^\circ \] and use the obtained base value into this.

Complete step-by-step answer:
First, we will draw the figure to understand the question,

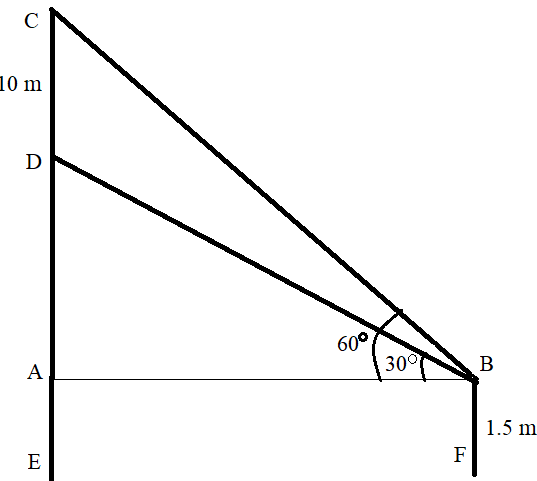
From the figure, the height of the building is CE.

As we know that, \[\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}\] .

We will first use this trigonometry ratio in triangle ABD and find the base AB then we will use this trigonometry ratio in the triangle ABC to find AC.

Now we are applying this trigonometric ratio into the triangle ABD and substituting the values into trigonometric ratio,

\[\tan 30^\circ = \dfrac{{{\text{AD}}}}{{{\text{AB}}}}\]

From this, we can find AB as,

 \[AB = \dfrac{{AD}}{{\tan 30^\circ }}\]

Now we are applying this trigonometric ratio into the triangle ABC and substituting the values into trigonometric ratio,

\[\tan 60^\circ = \dfrac{{{\text{AC}}}}{{{\text{AB}}}}\]

We know the value of AB, substituting the value of AB.

 \[
  \tan 60^\circ = \dfrac{{{\text{AC}}}}{{\left( {\dfrac{{AD}}{{\tan 30^\circ }}} \right)}} \\
   = \dfrac{{{\text{AC}}\tan 30^\circ }}{{AD}} \\
\]

From the figure, AC is sum of AD and DC. Replacing AC by \[AD + CD\],

\[\tan 60^\circ = \dfrac{{\left( {AD + CD} \right)\tan 30^\circ }}{{AD}}\]

Substituting the value of CD,

\[
  \tan 60^\circ = \dfrac{{\left( {AD + 10} \right)\tan 30^\circ }}{{AD}} \\
  \dfrac{{\tan 60^\circ }}{{\tan 30^\circ }} = \dfrac{{AD + 10}}{{AD}} \\
\]

As we know \[\tan 30^\circ = \dfrac{{\text{1}}}{{\sqrt 3 }}\] and \[\tan 60^\circ = \sqrt 3 \], substituting these values,

\[
  \dfrac{{\sqrt 3 }}{{\left( {\dfrac{{\text{1}}}{{\sqrt 3 }}} \right)}} = \dfrac{{AD + 10}}{{AD}} \\
  \dfrac{{\sqrt 3 \cdot \sqrt 3 }}{1} = \dfrac{{AD + 10}}{{AD}} \\
  3 = \dfrac{{AD + 10}}{{AD}} \\
\]

Now solve for AD,

\[
  3AD = AD + 10 \\
  3AD - AD = 10 \\
  2AD = 10 \\
  AD = \dfrac{{10}}{2} \\
  AD = 5 \\
\]

Now we know the height AD, DC and AE. Adding all these to find the height of the tower,

\[
  AE + AD + DC = 1.5 + 5 + 10 \\
   = 16.5 \\
\]

Thus, the height of the building is \[16.5\] m.

Note:
Any of the trigonometric functions can be used to find the answer but while solving these types of questions we have to first focus on “what we have to find” and then on “what data we have” so make our calculation shorter.