Question

A $15.0\mu F$ capacitor is connected to a 220 V, 50 Hz source. Find the capacitive reactance and the current (rms and peak) in the circuit. If the frequency is doubled. What happens to the capacitive reactance and current?

Answer 1

Hint: Reactance is a term used when we talk about the resistance provided by the capacitor or inductor in a circuit.
RMS stands for Root Mean Square value and the electricity that is supplied in homes have root mean square value of current as well as voltage.
Peak is the maximum value of current that can be passed in the circuit.

Formulas to be used:
${X_C} = \dfrac{1}{{\omega C}}$
$\omega = 2\pi \nu $
V = IR
Relationship between ${I_{rms}}$ and ${I_0}$:
${I_0} = \sqrt 2 {I_{rms}}$

Complete step by step answer:

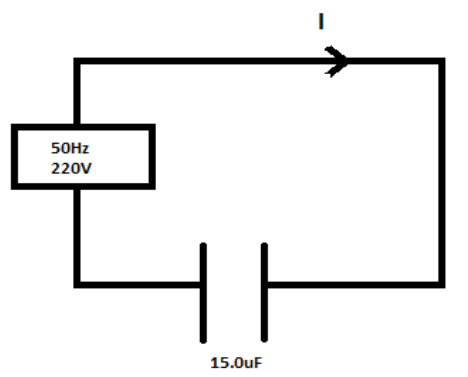
Given:
Capacitance (C) = $15.0\mu F$
Root mean square of voltage (\[{V_{rms}}\]) = 220 V
Frequency $\left( \nu \right)$ = 50 Hz
To find:
Capacitive reactance $({X_C})$ = ?
Root mean square value of current $\left( {{I_{rms}}} \right)$ = ?
Peak value of current $\left( {{I_0}} \right)$ = ?
i) Now,
 ${X_C} = \dfrac{1}{{\omega C}}$ ___________ (1)
  where,
${\omega _C}$is the angular velocity of the capacitor and is also equal to $2\pi \nu $
C = Capacitance
Substituting this in (1):
${X_C} = \dfrac{1}{{2\pi \nu C}}$ ______ (2)
${X_C} = \dfrac{1}{{2(3.14)(50)(15 \times {{10}^{ - 6}})}}$ [ As $\nu $ = 50 Hz , C = $15.0\mu F$ and $\pi $ = 3.14 ]

${X_C} = \dfrac{{{{10}^6} \times {{10}^2}}}{{2 \times 314 \times 50 \times 15}}$ [ taking all the powers of 10 in numerator]

 ${X_C} = \dfrac{{{{10}^8}}}{{471 \times {{10}^3}}}$
${X_C} = 212.3$
As it is a type of resistance its unit will be ohms$\left( \Omega \right)$
🡪Therefore, the value of capacitive reactance $212.3\Omega $
ii) From ohm’s law, we know:
V = IR
This gives,
ii) \[{I_{rms}} = \dfrac{{{V_{rms}}}}{{{X_c}}}\] __________ (3)
 Here current $\left( {{I_{rms}}} \right)$ and voltage\[({V_{rms}})\] are root mean square values and the resistance is only by capacitor$\left( {{X_c}} \right)$.
Substituting the values of \[{V_{rms}}\] and ${X_c}$, we get:
\[{I_{rms}} = \dfrac{{220}}{{212.3}}\]
\[{I_{rms}} = 1.04\]
SI unit of current is ampere (A)
🡪Therefore, Root mean square value of current is 1.04 A.

iii) Relationship between root mean square and peak value of current is:
${I_0} = \sqrt 2 {I_{rms}}$
Substituting the value of \[{I_{rms}}\], we get:
${I_0} = \sqrt 2 \times 1.04$
${I_0} = 1.465A$
🡪Therefore, the value peak current is 1.04 A.
iv) The relationships that can be deduced from (2) and (3) are:
${X_C} \propto \dfrac{1}{\nu }$ and $I \propto \dfrac{1}{{{X_C}}}$
According to the question, when the frequency is doubled:
$\nu = 2\nu $
$ \Rightarrow {X_C} \to \dfrac{{{X_C}}}{2}$
And
$I = 2I$
Therefore, if the frequency is doubled, the capacitive reactance reduces to half and the current is doubled.

Note:when more resistances are present in the circuit, in eqn (3) instead of directly writing the resistances we use impedance represented by Z. it is similar to resistance but different because it takes the reactance of capacitor and inductor in the circuit as well. Its SI units are ohm $\left( \Omega \right)$.
In case of direct proportionality, with the increase in one quantity the other quantity is also increased and in case inverse proportionality, with the increase in one quantity the other quantity is decreased.