Question

A 4 cm cube is cut into 1 cm cubes. Calculate the total surface area of all the small cubes.

Answer 1

Hint: Volume of a cube is \[{{a}^{3}}\] where \[a\] is the edge of the cube. So, we will calculate the volume of the cube for 4 cm and 1 cm and then use these two volumes to get the number of cubes of 1 cm edge.

Complete step-by-step answer:
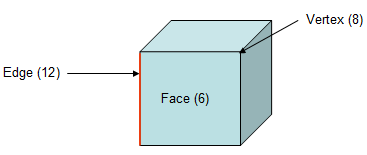
Before proceeding with the question we should know about cube. A cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. It has 6 faces, 12 edges, and 8 vertices.

Volume of a cube \[=V={{a}^{3}}........(1)\]

So now finding the volume of a 4 cm cube by putting \[a=4\,cm\] in equation (1) we get,

\[\Rightarrow V={{4}^{3}}=64\,c{{m}^{3}}..........(2)\]

As it is mentioned in the question that a 4 cm cube is cut into 1 cm cubes, so now finding the volume of a 1 cm cube by putting \[a=1\,cm\] in equation (1) we get,

\[\Rightarrow V={{1}^{3}}=1\,c{{m}^{3}}.........(3)\]

If we divide the volume of a 4 cm cube by the volume of a 1 cm cube we get the total number of 1 cm cubes. So for doing this, we divide equation (2) by equation (3) and we get,

Total number of 1 cm cubes \[=\dfrac{64}{1}=64.........(4)\]

Surface area of a cube \[=6\times {{a}^{2}}.......(5)\]

So now finding the surface area of a 1 cm cube by putting \[a=1\]cm in equation (5) we get,

Surface area of a 1 cm cube \[=6\times {{1}^{2}}=6\,c{{m}^{2}}.........(6)\]

Now by multiplying equation (4) with equation (6) we get,

Total surface area of all 64 small cubes \[=64\times 6\,c{{m}^{2}}=384\,c{{m}^{2}}\]

Hence the answer is \[384\,c{{m}^{2}}\].

Note: Remembering the formula of volume and surface area of a cube is the key here. We can make a mistake in a hurry in calculating the total number of 1 cm cubes. And as we are calculating area and unit of area is \[c{{m}^{2}}\] so we should not forget to write the unit otherwise marks will be deducted.