
A 5m wide cloth is used to make a conical tent of base diameter
Answer
412.5k+ views
Hint: In the given question we have to find the cost of the cloth and for that, we need to find the length of the cloth. As already given in the question, that cloth is used to make a conical (conical means that it is in the shape of a cone) tent that means the curved surface area of the conical tent is equal to the area of cloth. We can find the slant height of the conical tent using the information provided in the question. And from that, we can calculate the curved surface area of a conical tent which is equal to the area of cloth. From the area of cloth, we can calculate the length of cloth by using the formula of area of rectangle. Now, we have found the length of cloth so we can easily calculate the cost of cloth.
Formulae used:
The curved surface area of cone =
Slant height of cone
Area of rectangle = length
Complete step-by-step solution:
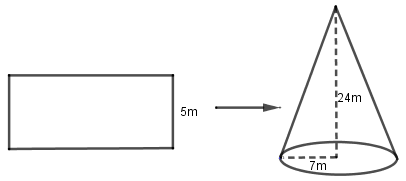
Given, Diameter of the conical tent =
Now, the tent is in the shape of a cone. Let its dimensions be radius
Now, for a cone relation between the radius, slant height and height is given by
Using above relation, we can find the value of slant height of tent
Substitute the values of radius and height.
On solving square, we get
On solving square root, we get
Then, the curved surface area of tent = curved surface area of cone =
It is given that conical tent is made from cloth, then
Area of cloth = Curved surface area of tent
Therefore, area of cloth
Length ×breadth
As already given in the question cost of
Cost of
Therefore, cost of
Note: The key concept to solve this type of question is to learn the formulas of different shapes. Students must know where to use total surface area and where to use the curved surface area for that to read the question carefully. Write length only in positive value because length can’t be negative. Students should be careful about the unit.
Formulae used:
The curved surface area of cone =
Slant height of cone
Area of rectangle = length
Complete step-by-step solution:

Given, Diameter of the conical tent =
Now, the tent is in the shape of a cone. Let its dimensions be radius
Now, for a cone relation between the radius, slant height and height is given by
Using above relation, we can find the value of slant height of tent
Substitute the values of radius and height.
On solving square, we get
On solving square root, we get
Then, the curved surface area of tent = curved surface area of cone =
It is given that conical tent is made from cloth, then
Area of cloth = Curved surface area of tent
Therefore, area of cloth
Length ×breadth
As already given in the question cost of
Cost of
Therefore, cost of
Note: The key concept to solve this type of question is to learn the formulas of different shapes. Students must know where to use total surface area and where to use the curved surface area for that to read the question carefully. Write length only in positive value because length can’t be negative. Students should be careful about the unit.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Discuss the main reasons for poverty in India




