
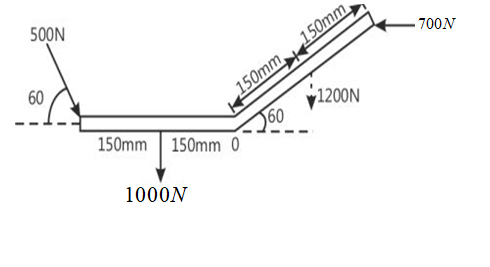
(a) A system of forces acting on a bell crank is as shown. Determine the magnitude, direction, and the point of application of the resultant w.r.t. 'O'
(b) Also, find the location of the resultant on the horizontal arm of the lever.

Answer
390.3k+ views
1 likes
Hint: The first part of the question asks us to find the magnitude of the resultant force. For that, we need to first find the resultant force along the x-direction and the y-direction separately, and then we need to substitute this in the resultant force formula. And then using the resultant at x-axis and y-axis and also using the angle we can draw the direction of the resultant force. And then for the second part of the question, we need Varignon's theorem.
Complete Step By Step Answer:
First, we need to find the forces that are acting in the horizontal directions. We can see that
Therefore,
Therefore the direction of the resultant force in the x-axis is towards the left-hand side since there is a negative sign.
Now we can find the net force acting in the downward direction. Similarly, the force that is divided into horizontal and vertical directions, the vertical component will come into this downward direction acting forces.
Therefore this vertical force acts in the downward direction.
The formula for the resultant force is given by,
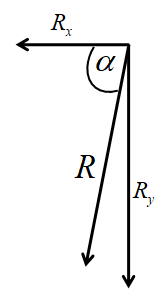
Now we need to find the angle of inclination for the resultant force with respect to O.
We can take the angle as
Now if we draw the components of resultant force in the x and y-axis we have also to find the angle and this angle is with respect to the horizontal direction. Therefore the direction of the resultant force will be shown in the below diagram.
Now we need to find the distance between the point of application of the resultant force and point O. Let this distance be x. We can find this by using varignon’s theorem.
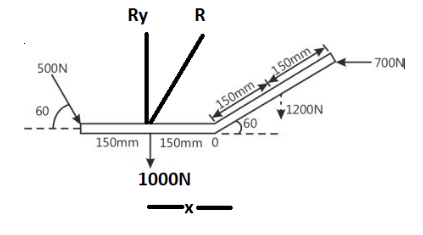
The varignon’s theorem states that the torque of the resultant of any number of forces about any point is equal to the algebraic sum of the torque of its components about the same point.
The torque can be calculated by the force multiplied by its distance.
Now the resultant force is resolved into its vertical component and this vertical component multiplied by the distance x gives a torque of the resultant force.
We already found the magnitude of
Note:
Varignon’s theorem can be used in order to replace the sum of each of the moments produced by the forces of the system that compose it by the moment of resultant when the resultant force of a system is known. While calculating the distance between the point of application of the resultant force and the point O that is while using varignon’s theorem we have used the negative sign for some forces and positive sign for some forces this is because we use the negative sign for anti-clockwise direction and positive sign for clockwise direction.
Complete Step By Step Answer:
First, we need to find the forces that are acting in the horizontal directions. We can see that
Therefore,
Therefore the direction of the resultant force in the x-axis is towards the left-hand side since there is a negative sign.
Now we can find the net force acting in the downward direction. Similarly, the force that is divided into horizontal and vertical directions, the vertical component will come into this downward direction acting forces.
Therefore this vertical force acts in the downward direction.
The formula for the resultant force is given by,
Now we need to find the angle of inclination for the resultant force with respect to O.
We can take the angle as
Now if we draw the components of resultant force in the x and y-axis we have also to find the angle and this angle is with respect to the horizontal direction. Therefore the direction of the resultant force will be shown in the below diagram.

Now we need to find the distance between the point of application of the resultant force and point O. Let this distance be x. We can find this by using varignon’s theorem.

The varignon’s theorem states that the torque of the resultant of any number of forces about any point is equal to the algebraic sum of the torque of its components about the same point.
The torque can be calculated by the force multiplied by its distance.
Now the resultant force is resolved into its vertical component and this vertical component multiplied by the distance x gives a torque of the resultant force.
We already found the magnitude of
Note:
Varignon’s theorem can be used in order to replace the sum of each of the moments produced by the forces of the system that compose it by the moment of resultant when the resultant force of a system is known. While calculating the distance between the point of application of the resultant force and the point O that is while using varignon’s theorem we have used the negative sign for some forces and positive sign for some forces this is because we use the negative sign for anti-clockwise direction and positive sign for clockwise direction.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




