Answer
Verified432.6k+ views
Hint: We need to find the effective lengths of the side cd initially and finally as the angle is changed. Next, an energy conservation formula is used for the above question. The total energy of the system initially must be equal to the total energy after the angle is changed.
Complete step by step answer:
The given system can be visualized as follows:
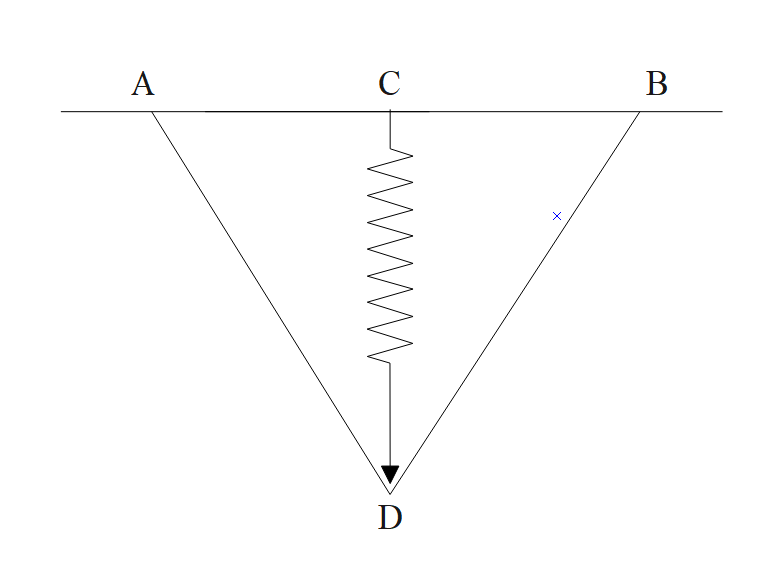
Let us first find out the effective length of the side cd before and after the angle cad is changed,
Initially, the length of side cd will be,
$CD=L\sin {{30}^{0}}=\dfrac{L}{2}$
Next, when the angle is changed, the new length of side cd will be
$CD=L\sin {{45}^{0}}=\dfrac{L}{\sqrt{2}}$
Now, the total energy of the system before the change is equal to,
Spring force+ kinetic energy.
$\dfrac{1}{2}k{{x}^{2}}+\dfrac{1}{2}m{{v}^{2}}$
As the value x in the above formula is the change in the length of the spring,
X will be equal to,
$x=\dfrac{L}{\sqrt{2}}-\dfrac{L}{2}$
Now, the total energy after the change in the angle will be,
$mgx=mg(\dfrac{L}{\sqrt{2}}-\dfrac{L}{2})$
As energy is conserved in the universe,
$\begin{align}
& \dfrac{1}{2}k{{(\dfrac{L}{\sqrt{2}}-\dfrac{L}{2})}^{2}}+\dfrac{1}{2}m{{v}^{2}}=mg(\dfrac{L}{\sqrt{2}}-\dfrac{L}{2}) \\
& \Rightarrow v={{[gL(\sqrt{2}-1)-\dfrac{K{{L}^{2}}}{4m}{{(\sqrt{2}-1)}^{2}}]}^{\dfrac{1}{2}}} \\
\end{align}$
Hence, we can find the velocity of the block in such a way.
Additional information:
Spring is a tool used daily by many of us and their inertia is frequently neglected by assuming it as massless. It’s an extremely casual activity that a spring when strained, undergoes displacement when it is compacted it gets compressed and when it is free it comes to its equilibrium position. This fact tells us that spring exerts an equal as well as an opposite force on a body which compresses or stretches it.
Note: The spring constant will depend on the stiffness of the spring material, the thickness of the wire from which the spring is wound and, the diameter of the ruins of the coil when we deal with a coil spring. The spring content and the length of the spring are inverse proportional to each other. The larger the spring constant, the smaller the extension that a given force creates.
Complete step by step answer:
The given system can be visualized as follows:
Let us first find out the effective length of the side cd before and after the angle cad is changed,
Initially, the length of side cd will be,
$CD=L\sin {{30}^{0}}=\dfrac{L}{2}$
Next, when the angle is changed, the new length of side cd will be
$CD=L\sin {{45}^{0}}=\dfrac{L}{\sqrt{2}}$
Now, the total energy of the system before the change is equal to,
Spring force+ kinetic energy.
$\dfrac{1}{2}k{{x}^{2}}+\dfrac{1}{2}m{{v}^{2}}$
As the value x in the above formula is the change in the length of the spring,
X will be equal to,
$x=\dfrac{L}{\sqrt{2}}-\dfrac{L}{2}$
Now, the total energy after the change in the angle will be,
$mgx=mg(\dfrac{L}{\sqrt{2}}-\dfrac{L}{2})$
As energy is conserved in the universe,
$\begin{align}
& \dfrac{1}{2}k{{(\dfrac{L}{\sqrt{2}}-\dfrac{L}{2})}^{2}}+\dfrac{1}{2}m{{v}^{2}}=mg(\dfrac{L}{\sqrt{2}}-\dfrac{L}{2}) \\
& \Rightarrow v={{[gL(\sqrt{2}-1)-\dfrac{K{{L}^{2}}}{4m}{{(\sqrt{2}-1)}^{2}}]}^{\dfrac{1}{2}}} \\
\end{align}$
Hence, we can find the velocity of the block in such a way.
Additional information:
Spring is a tool used daily by many of us and their inertia is frequently neglected by assuming it as massless. It’s an extremely casual activity that a spring when strained, undergoes displacement when it is compacted it gets compressed and when it is free it comes to its equilibrium position. This fact tells us that spring exerts an equal as well as an opposite force on a body which compresses or stretches it.
Note: The spring constant will depend on the stiffness of the spring material, the thickness of the wire from which the spring is wound and, the diameter of the ruins of the coil when we deal with a coil spring. The spring content and the length of the spring are inverse proportional to each other. The larger the spring constant, the smaller the extension that a given force creates.