
A, B and C represents switches in ‘on’ position and A’, B’ and C’ represents them in ‘off’ position. Construct a switching circuit representing the polynomial
Answer
525.3k+ views
Hint: Use the property of Boolean algebra which are
Complete step-by-step answer:
Given polynomial is
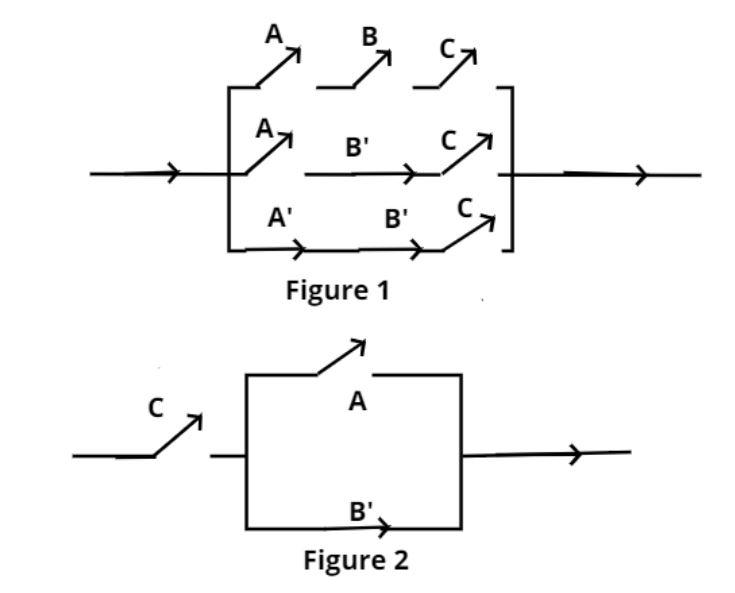
Now we have to prove that
Consider L.H.S
Take AC common from first two terms
As we know in Boolean algebra value of
Now take C as common
Now
Because we know in Boolean algebra the value of
So,
Therefore
Therefore from equation (1)
Now as we know in Boolean algebra value of
=R.H.S
Hence Proved.
And the equivalent representation is shown in figure (2), where A, B and C represents switches in ‘on’ position and A’, B’ and C’ represents them in ‘off’ position.
Note: Whenever we face such types of questions always remember some of the basic properties of the Boolean algebra which is stated above then using these properties simplify the given polynomial, we will get the required answer.
Complete step-by-step answer:
Given polynomial is

Now we have to prove that
Consider L.H.S
Take AC common from first two terms
As we know in Boolean algebra value of
Now take C as common
Now
Because we know in Boolean algebra the value of
So,
Therefore
Therefore from equation (1)
Now as we know in Boolean algebra value of
=R.H.S
Hence Proved.
And the equivalent representation is shown in figure (2), where A, B and C represents switches in ‘on’ position and A’, B’ and C’ represents them in ‘off’ position.
Note: Whenever we face such types of questions always remember some of the basic properties of the Boolean algebra which is stated above then using these properties simplify the given polynomial, we will get the required answer.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




