
A balanced Wheatstone's bridge is shown in the figure. Find the value of the currents ${i_1}$ and ${i_2}$.
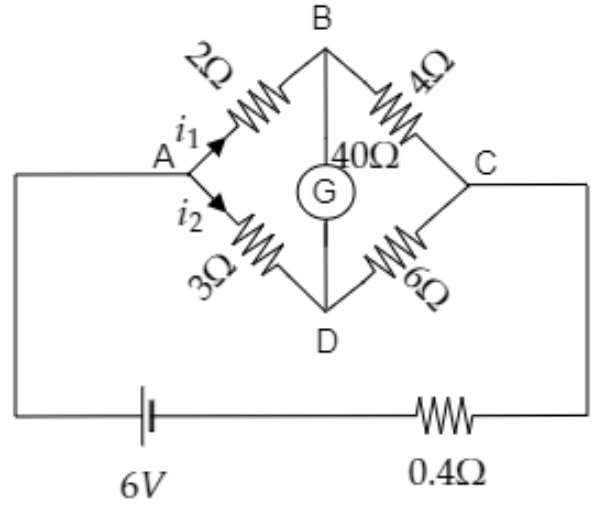
A) $0.9{\text{A}}$ and $0.6{\text{A}}$
B) $0.3{\text{A}}$ and $0.2{\text{A}}$
C) $0.5{\text{A}}$ and $0.7{\text{A}}$
D) $0.7{\text{A}}$ and $0.6{\text{A}}$
Answer
232.8k+ views
Hint: In a balanced Wheatstone's bridge, the ratio of the resistances of the two arms will be the same. Here branches ABC and ADC are connected in parallel but the resistors in each branch form a series connection. So we can find the effective resistance of the circuit which will give us the total current in the circuit. The currents ${i_1}$ and ${i_2}$ can be then found out using the balance condition of the bridge.
Formulae used:
The effective resistance when two resistors are connected in series is given by, ${R_{eff}} = {R_1} + {R_2}$ where ${R_1}$ and ${R_2}$ are the resistances of the two resistors.
The effective resistance when two resistors are connected in parallel is given by, ${R_{eff}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$ where ${R_1}$ and ${R_2}$ are the resistances of the two resistors.
The current through a circuit is given by, $I = \dfrac{V}{{{R_{eff}}}}$ where ${R_{eff}}$ is the effective resistance of the circuit and $V$ is the voltage across the circuit.
Complete step by step answer:
Sketch the given circuit diagram and list its parameters.
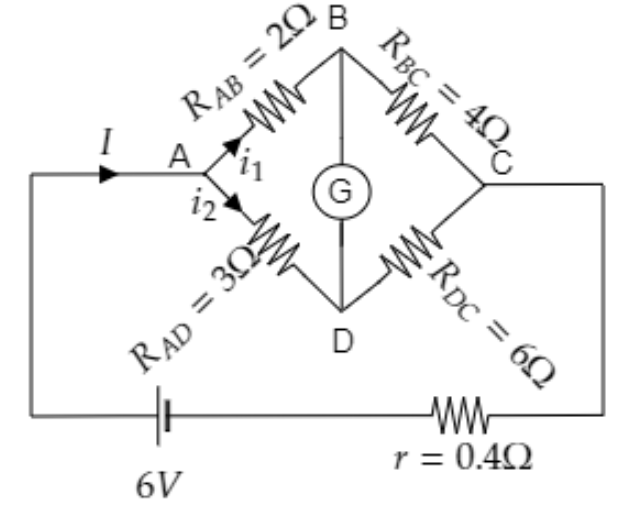
From the above diagram we have, ${R_{AD}} = 3\Omega $ , ${R_{DC}} = 6\Omega $ , ${R_{AB}} = 2\Omega $ and ${R_{BC}} = 4\Omega $ .
The internal resistance of the battery is $r = 0.4\Omega $ .
The emf of the battery is $V = 6{\text{V}}$ .
Here ${i_1}$ is the current through ABC and ${i_2}$ is the current through ADC.
Let $I$ be the total current through the circuit.
Obtain the effective resistances of the two branches to find the effective resistance of the circuit.
In branch ADB, ${R_{AD}}$ and ${R_{DC}}$ are connected in series and so the effective resistance of branch ADB will be ${R_{ADC}} = {R_{AD}} + {R_{DC}}$ ------- (1)
Substituting ${R_{AD}} = 3\Omega $ and ${R_{DC}} = 6\Omega $ in equation (1) we get, ${R_{ADC}} = 3 + 6 = 9\Omega $
So the effective resistance of branch ADC is ${R_{ADC}} = 9\Omega $ .
Similarly, in branch ABC, ${R_{AB}} = 2\Omega $ and ${R_{BC}} = 4\Omega $ are connected in series and so the effective resistance of branch ABC will be ${R_{ABC}} = 2 + 4 = 6\Omega $ .
Now the reduced circuit is given below.
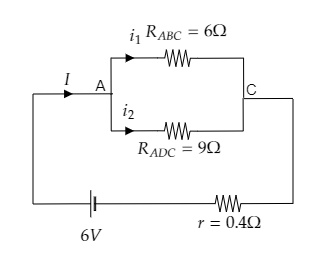
In this circuit ${R_{ADC}} = 9\Omega $ and ${R_{ABC}} = 6\Omega $ are connected in parallel and the internal resistance of the battery is connected in series with it.
So the effective resistance of the circuit will be ${R_{eff}} = \dfrac{{{R_{ADC}}{R_{ABC}}}}{{{R_{ADC}} + {R_{ABC}}}} + r$ -------- (2)
Substituting ${R_{ADC}} = 9\Omega $ , ${R_{ABC}} = 6\Omega $ and $r = 0.4\Omega $ in equation (2) we get, ${R_{eff}} = \dfrac{{9 \times 6}}{{9 + 6}} + 0.4 = 4\Omega $
Thus the total resistance of the circuit is ${R_{eff}} = 4\Omega $ .
Using Ohm’s law obtains the total current through the circuit.
Ohm’s law gives the current through the given circuit as $I = \dfrac{V}{{{R_{eff}}}}$ -------- (3)
Substituting for ${R_{eff}} = 4\Omega $ and $V = 6{\text{V}}$ in equation (3) we get, $I = \dfrac{6}{4} = 1.5{\text{A}}$
Thus the current through the circuit is $I = 1.5{\text{A}}$ .
Using Kirchoff’s junction rule and the balanced condition of the bridge we can find the currents ${i_1}$ and ${i_2}$ .
According to Kirchoff’s junction rule at point A, the total current $I$ splits into the currents ${i_1}$ and ${i_2}$ .
i.e., $I = {i_1} + {i_2}$ ------- (4)
Also, the given Wheatstone's bridge is said to be balanced.
$ \Rightarrow {i_2}{R_{AD}} = {i_1}{R_{AB}}$ --------- (5)
Substituting for ${R_{AB}} = 2\Omega $ and ${R_{AD}} = 3\Omega $ in equation (5) we get, $3{i_2} = 2{i_1}$
$ \Rightarrow {i_2} = \dfrac{{2{i_1}}}{3}$ ------- (6)
Substituting equation (6) in (4) we get, $I = {i_1} + \dfrac{{2{i_1}}}{3} = \dfrac{{5{i_2}}}{3}$
$ \Rightarrow {i_1} = \dfrac{{3I}}{5}$ and on substituting for $I = 1.5{\text{A}}$ we get, ${i_1} = \dfrac{{3 \times 1.5}}{5} = 0.9{\text{A}}$
Then back-substituting ${i_1} = 0.9{\text{A}}$ in equation (6) we get, ${i_2} = \dfrac{{2 \times 0.9}}{3} = 0.6{\text{A}}$
Thus the values of the currents are ${i_1} = 0.9{\text{A}}$ and ${i_2} = 0.6{\text{A}}$.
So the correct option is A.
Note: Here the Wheatstone’ bridge is mentioned to be a balanced bridge. In a balanced bridge, the potential drop at points C and D in the given circuit diagram will be the same. This is given by equation (5). Also since the potential drop at C and D are the same, the potential difference between these two points will be zero and so no current will flow through the galvanometer.
Formulae used:
The effective resistance when two resistors are connected in series is given by, ${R_{eff}} = {R_1} + {R_2}$ where ${R_1}$ and ${R_2}$ are the resistances of the two resistors.
The effective resistance when two resistors are connected in parallel is given by, ${R_{eff}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$ where ${R_1}$ and ${R_2}$ are the resistances of the two resistors.
The current through a circuit is given by, $I = \dfrac{V}{{{R_{eff}}}}$ where ${R_{eff}}$ is the effective resistance of the circuit and $V$ is the voltage across the circuit.
Complete step by step answer:
Sketch the given circuit diagram and list its parameters.

From the above diagram we have, ${R_{AD}} = 3\Omega $ , ${R_{DC}} = 6\Omega $ , ${R_{AB}} = 2\Omega $ and ${R_{BC}} = 4\Omega $ .
The internal resistance of the battery is $r = 0.4\Omega $ .
The emf of the battery is $V = 6{\text{V}}$ .
Here ${i_1}$ is the current through ABC and ${i_2}$ is the current through ADC.
Let $I$ be the total current through the circuit.
Obtain the effective resistances of the two branches to find the effective resistance of the circuit.
In branch ADB, ${R_{AD}}$ and ${R_{DC}}$ are connected in series and so the effective resistance of branch ADB will be ${R_{ADC}} = {R_{AD}} + {R_{DC}}$ ------- (1)
Substituting ${R_{AD}} = 3\Omega $ and ${R_{DC}} = 6\Omega $ in equation (1) we get, ${R_{ADC}} = 3 + 6 = 9\Omega $
So the effective resistance of branch ADC is ${R_{ADC}} = 9\Omega $ .
Similarly, in branch ABC, ${R_{AB}} = 2\Omega $ and ${R_{BC}} = 4\Omega $ are connected in series and so the effective resistance of branch ABC will be ${R_{ABC}} = 2 + 4 = 6\Omega $ .
Now the reduced circuit is given below.

In this circuit ${R_{ADC}} = 9\Omega $ and ${R_{ABC}} = 6\Omega $ are connected in parallel and the internal resistance of the battery is connected in series with it.
So the effective resistance of the circuit will be ${R_{eff}} = \dfrac{{{R_{ADC}}{R_{ABC}}}}{{{R_{ADC}} + {R_{ABC}}}} + r$ -------- (2)
Substituting ${R_{ADC}} = 9\Omega $ , ${R_{ABC}} = 6\Omega $ and $r = 0.4\Omega $ in equation (2) we get, ${R_{eff}} = \dfrac{{9 \times 6}}{{9 + 6}} + 0.4 = 4\Omega $
Thus the total resistance of the circuit is ${R_{eff}} = 4\Omega $ .
Using Ohm’s law obtains the total current through the circuit.
Ohm’s law gives the current through the given circuit as $I = \dfrac{V}{{{R_{eff}}}}$ -------- (3)
Substituting for ${R_{eff}} = 4\Omega $ and $V = 6{\text{V}}$ in equation (3) we get, $I = \dfrac{6}{4} = 1.5{\text{A}}$
Thus the current through the circuit is $I = 1.5{\text{A}}$ .
Using Kirchoff’s junction rule and the balanced condition of the bridge we can find the currents ${i_1}$ and ${i_2}$ .
According to Kirchoff’s junction rule at point A, the total current $I$ splits into the currents ${i_1}$ and ${i_2}$ .
i.e., $I = {i_1} + {i_2}$ ------- (4)
Also, the given Wheatstone's bridge is said to be balanced.
$ \Rightarrow {i_2}{R_{AD}} = {i_1}{R_{AB}}$ --------- (5)
Substituting for ${R_{AB}} = 2\Omega $ and ${R_{AD}} = 3\Omega $ in equation (5) we get, $3{i_2} = 2{i_1}$
$ \Rightarrow {i_2} = \dfrac{{2{i_1}}}{3}$ ------- (6)
Substituting equation (6) in (4) we get, $I = {i_1} + \dfrac{{2{i_1}}}{3} = \dfrac{{5{i_2}}}{3}$
$ \Rightarrow {i_1} = \dfrac{{3I}}{5}$ and on substituting for $I = 1.5{\text{A}}$ we get, ${i_1} = \dfrac{{3 \times 1.5}}{5} = 0.9{\text{A}}$
Then back-substituting ${i_1} = 0.9{\text{A}}$ in equation (6) we get, ${i_2} = \dfrac{{2 \times 0.9}}{3} = 0.6{\text{A}}$
Thus the values of the currents are ${i_1} = 0.9{\text{A}}$ and ${i_2} = 0.6{\text{A}}$.
So the correct option is A.
Note: Here the Wheatstone’ bridge is mentioned to be a balanced bridge. In a balanced bridge, the potential drop at points C and D in the given circuit diagram will be the same. This is given by equation (5). Also since the potential drop at C and D are the same, the potential difference between these two points will be zero and so no current will flow through the galvanometer.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Understanding the Electric Field of a Uniformly Charged Ring

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance




