Question

A ball falls on an inclined plane of inclination $\theta $, from a height h above the point of impact and makes a perfectly elastic collision. Where will it be on the plane again?

Answer 1

Hint: In questions like this, always make the use of the three kinematic equations. If projectile motion is involved, then divide the velocity into its component then analyse each component separately. Both components will have one quantity in common i.e. time. Dealing with the motion in one dimension is easier than two-dimensional motion.

Complete step-by-step answer:
Let the ball start its motion at time t=0. The force of gravity will accelerate it. Therefore, it will come down with an acceleration of g i.e. acceleration due gravity. Let its velocity just before hitting the plane be ‘v’. Let us first calculate the value of this velocity. Use the kinematic equation, $2as={{v}^{2}}-{{u}^{2}}$. Here, $a=-g$, $s=-h$ , $u=0$ and we have to find v.
$\Rightarrow 2(-g)(-h)={{v}^{2}}-0\Rightarrow v=\sqrt{2gh}$. …….(i)
The velocity of the ball just before hitting the plane is $\sqrt{2gh}$, directed downwards.

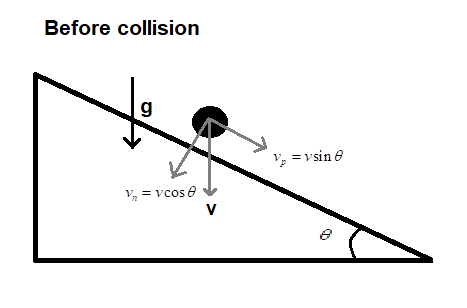
Now, divide this velocity into its components such that one component is normal to the plane (say vn) and the other component is along the plane (say vp). After using geometry, we can see that ${{v}_{p}}=v\sin \theta $ and ${{v}_{n}}=v\cos \theta $. When the ball hits the plane, the plane will exert a reaction force on the ball, which is normal to the plane. Since, this force is normal to the plane, it will only affect the perpendicular component (vn) of the velocity (v) of the ball and because the collision is said to be elastic, the velocity after the collision will be equal to vn in magnitude but opposite in direction to vn (as shown in the figure below). Vp will remain the same after the collision.

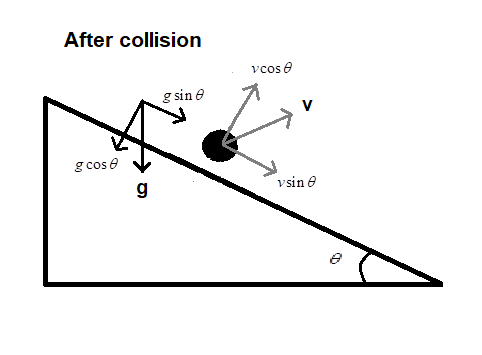
Now, the ball has a velocity whose components are $v\sin \theta $ and $v\cos \theta $as shown. Divide the ball into two balls. One ball (B1) moves parallel to the plane with velocity $v\sin \theta $ and the other ball (B2) moves normal to the plane with velocity $v\cos \theta $. Consider both the directions of the velocities as positive directions. B1 will have an acceleration of $g\sin \theta $ and B2 will have an acceleration of $g\cos \theta $, as shown in the figure.
The original ball will hit the plane again when the ball B2 hits the plane again. Let us calculate the time it takes for B2 to hit the plane again. Use the displacement equation, $s=ut+\dfrac{1}{2}a{{t}^{2}}$. Here, $s=0$, $u=v\cos \theta $, $a=-g\cos \theta $
Therefore, $0=(v\cos \theta )t+\dfrac{1}{2}(-g\cos \theta ){{t}^{2}}$
Take $\cos \theta $ as a common factor. $\Rightarrow 0=\cos \theta \left( (v)t+\dfrac{1}{2}(-g){{t}^{2}} \right)$
Therefore, $\left( (v)t+\dfrac{1}{2}(-g){{t}^{2}} \right)=0$ or $\cos \theta =0$. In this case, theta cannot be $90^o$. If theta is $90^o$, the ball will never hit the ball. If theta cannot be $90^o$ then $\cos \theta $ cannot be equal to zero.
Therefore, $\cos \theta =0$ is discarded.
Let us continue with $\left( (v)t+\dfrac{1}{2}(-g){{t}^{2}} \right)=0$.
Take t as a common term.
$\left( v+\dfrac{1}{2}(-g)t \right)t=0$. But t cannot be zero and therefore $\left( v+\dfrac{1}{2}(-g)t \right)=0$
$\Rightarrow v-\dfrac{1}{2}gt=0\Rightarrow t=\dfrac{2v}{g}$
That means the original ball takes a time of $t=\dfrac{2v}{g}$ to hit the plane again. To find how far did the original ball hit the place again, we will use the ball B1. When the original ball hits the plane again, B1 will reach at that point at the same time. So, let us calculate the distance travelled by B1 in time $t=\dfrac{2v}{g}$.
Again use the displacement equation, $s=ut+\dfrac{1}{2}a{{t}^{2}}$. Here, $u=v\sin \theta $, $a=g\sin \theta $ and $t=\dfrac{2v}{g}$.
Therefore, $s=(v\sin \theta )\left( \dfrac{2v}{g} \right)+\dfrac{1}{2}(g\sin \theta ){{\left( \dfrac{2v}{g} \right)}^{2}}$
$\Rightarrow s=\dfrac{2{{v}^{2}}\sin \theta }{g}+\dfrac{2{{v}^{2}}\sin \theta }{g}=\dfrac{4{{v}^{2}}\sin \theta }{g}$ ……(ii)
From the equation we know that $v=\sqrt{2gh}$. Substitute the value of v in equation (ii).
$\Rightarrow s=\dfrac{4{{v}^{2}}\sin \theta }{g}=\dfrac{4{{\left( \sqrt{2gh} \right)}^{2}}\sin \theta }{g}=8h\sin \theta $
Therefore, the ball will hit the place again at a distance of $s=8h\sin \theta $ from the previous point of impact.

Note: For calculating the velocity of the ball just before hitting the plane, we can also use the work energy theorem. Work energy theorem states that the amount of work done on a body is equal to the change in kinetic energy of the body. The ball came down in the direction of the gravitational force (mg) for a displacement of ‘h’. Therefore, work done by the gravity is $W=mgh$. This will be equal to the change in kinetic energy. $\Rightarrow W=\Delta K.E=K.{{E}_{f}}-K.{{E}_{i}}\Rightarrow mgh=\dfrac{1}{2}m{{v}^{2}}-0$
Therefore, $v=\sqrt{2gh}$.