Question

A ball is dropped on the ground from the height of 1m. The coefficient of restitution is 0.6. The height to which the ball will rebound is (in m)
A. 0.6
B. 0.4
C. 0.36
D. 0.16

Answer 1

Hint: We have a ball that is dropped from a height. The ball reaches the ground and rebounds. We need to find the height to which the ball rebounds. We know the equation for velocity of a body falling from a height and a relation between velocity and coefficient of restitution. Substituting values in these equations we get the required solution.

Formula Used:
Velocity of a body falling from a height ‘H’ is given by,
$v=\sqrt{2gH}$
Coefficient of restitution and velocity,
${{v}_{f}}=ev$

Complete step-by-step answer:

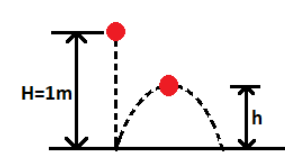
In the question a ball is dropped from a height 1m
This is the initial height of the ball.
Let us denote this height by ‘H’
H = 1m
The ball reaches the ground and bounces from the surface.
Let the height to which the ball rebounds be denoted as ‘h’
We know that when a body falls from a height ‘H’, the velocity of that body is given by the equation,
$v=\sqrt{2gH}$
In this case, value of H is 1m
Therefore, velocity of the ball will be
$v=\sqrt{2g}$
This is the velocity of the ball when it strikes the ground.
After striking the ground the ball will rebound with a velocity. Let this velocity be the final velocity.
Final velocity is given by the equation,
${{v}_{f}}=ev$, were ‘${{v}_{f}}$’ is final velocity, ‘e’ is coefficient of restitution and ‘v’ is the striking velocity.
When the ball strikes the ground and rebounds to a height h, the velocity with which the body rebounds, i.e. the final velocity will become,
${{v}_{f}}=\sqrt{2gh}$
Since ${{v}_{f}}=ev$, we get
 $\begin{align}
  & \sqrt{2gh}=e\sqrt{2g} \\
 & 2gh={{e}^{2}}2g \\
 & h={{e}^{2}} \\
\end{align}$
In the question we are given the value of coefficient of restitution, e = 0.6
Therefore the height to which the ball rebounds ‘h’ will become,
$\begin{align}
  & h={{0.6}^{2}} \\
 & h=0.36m \\
\end{align}$
Hence the correct answer is option C.

Note: When two objects collide, the coefficient of restitution is the ratio of the final velocity to the initial relative velocity of the two objects after collision.
In the case of a bouncing ball, the coefficient of restitution is calculated by taking the square root of the ratio of one bounce to the height of the next bounce.