Question

A ball of mass m is tied up with string and rotated along a horizontal circle of radius r. At an instant, its velocity is v, and tension in the string is T. The force required for circular motion is:
A. $T - \dfrac{mv^2}{r}$
B. $T + \dfrac{mv^2}{r}$
C. $\dfrac{mv^2}{r}$
D. Zero

Answer 1

Hint: A body performing circular motion experiences a centripetal force towards the centre of the circle or if centripetal force is present, a body performs circular motion. This centripetal force can come from gravitational force or tension or other forces.

Complete step by step answer:
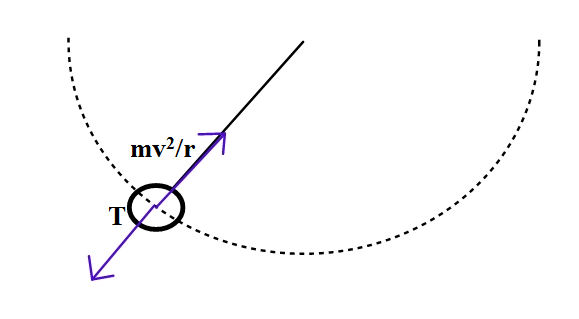
The word 'centripetal' itself means towards the centre. In our case, when a ball of mass m is tied up to the string and makes horizontal circular motion, the centripetal force acts towards the centre on the ball and the tension acts away from the center. Both the types of forces balance each other unless friction is also present. Therefore, the tension in the string is able to give us the required force for circular motion which is nothing but the centripetal force given by $mv^2/r$.

Therefore, the correct answer is option (C).

Additional information:
We analyse a situation where we increase the velocity of motion of the ball in its circular path. This will result in an increase in the centripetal force and hence, it will increase the tension in the string. When the tension in the string exceeds the elastic limit, the string breaks and circular motion is no longer observed. Therefore, we can say from here that more the tension the string is able to sustain, more velocity the ball can have in while circular motion.

Note:
The options can be a little confusing and one might choose the wrong answer if one does not know the definition of centripetal force. One should just pay attention to what is being asked at the end of the question. We are clearly asked the force required for circular motion which in itself is the definition of centripetal force.