Question

A barometer reads $76 cm$ of mercury. If the tube is gradually inclined at an angle of $ 60^\circ $ with vertical, keeping the open end immersed in the reservoir, the length of the mercury column will be
(A) 152 cm
(B) 72 cm
(C) 32 cm
(D) 38 cm

Answer 1

Hint: In order to solve the question, we will first resolve the vertical and horizontal components of the length of mercury occupies when it is tilt at an angle after then we will equate the vertical component angled mercury test tube with the height of straight test tube occupying the space.

Complete step by step answer:
In the question we are given a barometer which reads mercury in the test tube. If the tube is gradually inclined at an angle with vertical, keeping the open end immersed in the reservoir and we have to find the length of the mercury column
Original length which mercury column maintain = 76 cm
Tube is inclined at an angle = $ 60^\circ $

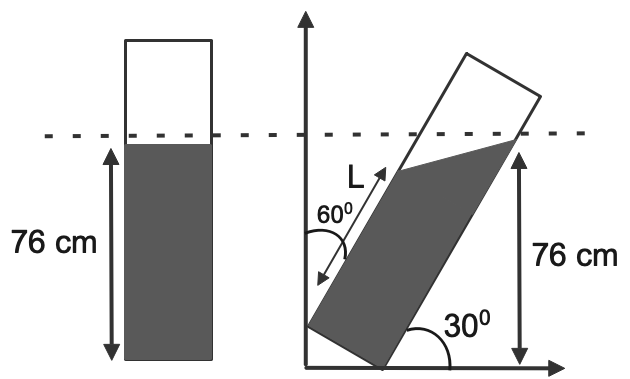
Let us assume the length of mercury occupied space at the angle be “L”
In the figure as we can see original vertical length which mercury occupies is 76 cm and when we tilt the test it laterally occupies the length “L”

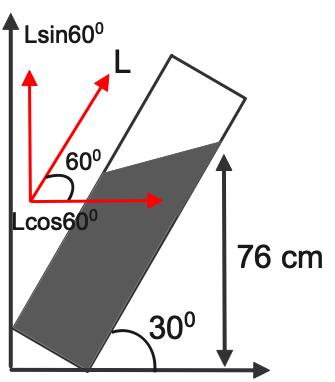
In the above figure we can see that “L” is resolved in the component now we will equate the vertical component of “L” with the height of straight test tube occupying the space
 $ L\sin 30^\circ = 76cm $
Value of $ \sin 30^\circ = \dfrac{1}{2} $
Now we will equate the value of $ \sin 30^\circ $ in the equation
 $ L \times \dfrac{1}{2} = 76cm $
Now we will take half on the other side which gives us the value of “L”
 $ L = 152cm $
Hence, the correct option is option (A) 152 cm .

Note:
There might be a chance of making mistakes by using the pressure equation in the question as it contains the physical quantity height but the height remains constant so the equation will be useless as the question involves basic trigonometry and the component resolving of angled segments.