Question

A battery of emf 10 V and internal resistance of 0.5 ohm is connected across a variable resistance R. The value of R for maximum power transfer is:
A. $0.5\Omega $
B. $1.00\Omega $
C. $2.0\Omega $
D. $0.25\Omega $

Answer 1

Hint: The internal resistance of a battery can be considered to be a resistance in series with the battery. This problem can be solved by finding out the relation between the current (I) and the emf (E) produced by the battery. Then this relation is used in the equation of power $\left( {{I}^{2}}R \right)$ consumed by R and differentiated with respect to R to get the maximum value and a value for R.
Formula used:
$V=IR$ --(Ohm’s Law)
where V is the potential drop across a resistor of resistance R and I is the current through it.
For a quantity y as a function of x, the maximum value of y is given by,
$\dfrac{dy}{dx}=0$
and, $\dfrac{{{d}^{2}}y}{d{{x}^{2}}}<0$ (for the value of x for which $\dfrac{dy}{dx}=0$)
For two resistances R and r in series, the equivalent resistance is given by,
${{R}_{equivalent}}=R+r$
The power consumed by a resistor R when a current I flows through it is given by,
$P={{I}^{2}}R$

Complete Step-by-Step solution:
This problem can be solved by finding out the relation between the current (I) and the emf (E) produced by the battery. Then this relation is used in the equation of power $\left( {{I}^{2}}R \right)$ consumed by R and differentiated with respect to R to get the maximum value and a value for R.
To find out the relation between the current and the emf, let us consider a simple circuit with a battery of emf E and internal resistance r, with a simple resistance R as shown below.

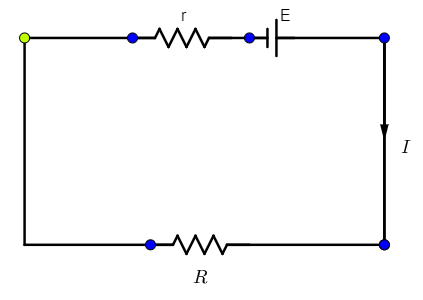
A current I flows through the circuit.
Now, the internal resistance of a battery can be considered to be a resistance in series with the battery.
Now, for two resistances R and r in series, the equivalent resistance is given by,
${{R}_{equivalent}}=R+r$ ----------------(1)
By, Ohm’s law, which states that the current flowing in a circuit is the ratio of the potential drop in the total circuit to the resistance of the total circuit,
$I=\dfrac{E}{{{R}_{equivalent}}}$ ----------------(2)
Putting (1) in (2),
$I=\dfrac{E}{R+r}$ -----------------(3)
Now, the power consumed by a resistor R when a current I flows through it is given by,
$P={{I}^{2}}R$ ------------------(4)
Therefore, using (4) and (3), the power dissipated by the battery is given by
${{\left( \dfrac{E}{R+r} \right)}^{2}}R=\dfrac{{{E}^{2}}R}{{{\left( R+r \right)}^{2}}}$ -----------------(5)
Now, For a quantity y as a function of x, the maximum value of y is given by,
$\dfrac{dy}{dx}=0$
and, $\dfrac{{{d}^{2}}y}{d{{x}^{2}}}<0$ (for the value of x for which$\dfrac{dy}{dx}=0$)
Therefore, to get the maximum of the power dissipated by R, we have to differentiate (5) with respect to R.
$\dfrac{d\dfrac{{{E}^{2}}R}{{{\left( R+r \right)}^{2}}}}{dR}=\dfrac{{{\left( R+r \right)}^{2}}\left( {{E}^{2}} \right)-{{E}^{2}}R\times 2\left( R+r \right)}{{{\left( R+r \right)}^{4}}}=\dfrac{{{E}^{2}}\left( R+r \right)\left( R+r-2R \right)}{{{\left( R+r \right)}^{4}}}=\dfrac{{{E}^{2}}\left( r-R \right)}{{{\left( R+r \right)}^{3}}}$ ------------------(6)
For maximum power, (6) = 0,
$\therefore \dfrac{{{E}^{2}}\left( r-R \right)}{{{\left( R+r \right)}^{3}}}=0$
$\therefore {{E}^{2}}=0$
or,
$r-R=0$
But, ${{E}^{2}}=0$ will mean $E=0$ which will clearly mean that no current flows in the circuit and power transfer is 0 (minimum). But, we want value for maximum power transfer. Hence,
$\therefore r-R=0$
$\therefore r=R$
There is no need for the second derivative test, since we have already determined for which values there will be a minima and for which one there will be a maxima.
Hence, for maximum power transfer $r=R$ , that is the value of the external load resistance must be equal to the value of the internal resistance of the battery.
Now, coming back to the values given in the question, the value of internal resistance is $0.5\Omega $. Therefore, for maximum power transfer the value of the external resistance R must also be equal to the internal resistance that is $0.5\Omega $.
Hence, the correct option is A) $0.5\Omega $.

Note: For questions that require to find out the maximum or minimum value of a quantity, it is always better to follow the above process, that is to first find a relation between two quantities in terms of a variable and then to differentiate the required equation with respect to the variable and equate to zero.
Doing the second derivative test is a good practice rather than jumping to conclusions after the first derivative test because the first derivative test yields the values for minima and maxima both. It is better to do the second derivative test and be sure rather than make overconfident silly mistakes.
However, in cases like this where the values for maxima and minima are very clear, even by applying common sense there is no need to do the second derivative test and waste time, especially in competitive exams.
Not only in the case of one external resistance, but, in general, if the total equivalent external resistance of the circuit is equal to the internal resistance of the battery, then the power transferred by the battery to the circuit will be maximum.