Question

A battery of emf \[12\,V\] and internal resistance \[2\,\Omega \] is connected with two resistors \[A\] and \[B\] of resistance \[4\Omega \] and \[6\,\Omega \] respectively joined in series. Find:
(i) Current in the circuit.
(ii) The terminal voltage of the cell.
(iii) The potential difference across the \[6\,\Omega \] resistor.
(iv) Electrical energy spent per minute in the \[4\,\Omega \] resistor.

Answer 1

Hint: To solve this problem, use Ohm’s law for an electric circuit. Ohm’s law is given by, \[V = IR\] where, \[V\] is the voltage across any circuit element, \[I\] is the current through it, \[R\] is the resistance of the element. The energy dissipated per second from a circuit element of resistance \[R\] is given by, \[P = {I^2}R\], where \[I\] is the current through the resistance.

Complete step by step answer:
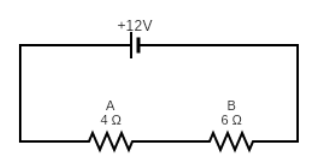
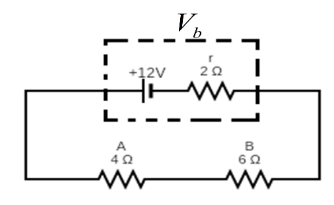
We know that Ohm's law for a circuit element in an electric circuit is given by, \[V = IR\]. Here, we have a battery of emf \[E = 12V\] with internal resistance \[r = 2\Omega \] is connected with two resistors \[{R_A} = 40\Omega \] and \[{R_B} = 60\Omega \]joined in series. So, circuits can also be drawn as follows.

(i) To find the current in the circuit at first we have to find the total resistance of the circuit.So, equivalent resistance of the circuit will be, \[{R_{eq}} = 4 + 6 + 2 = 10\] since all the resistances are connected in series. So, current through the circuit will be, \[I = \dfrac{E}{{{R_{eq}}}}\]
Putting values, we have, \[I = \dfrac{{12}}{{12}} = 1A\].
Hence, current through the circuit will be \[1A\].

(ii) We know that for an ideal cell/battery the terminal voltage is the same as the emf of the cell/battery but for a practical cell or battery the terminal voltage of a cell is the voltage across its terminals. Here, the battery has an internal resistance \[r = 2\Omega \] and that will lead to additional voltage drop across its terminals.So, the voltage drop due to the internal resistance is, \[V = Ir = 1 \times 2 = 2V\]
Hence, voltage across its terminal will be,
\[{V_b} = E - V\]
\[\therefore {V_b} = 12 - 2 = 10\,V\]
Hence, voltage across the terminal of the battery will be, \[10\,V\]

(iii) The potential difference across \[{R_B} = 6\,\Omega \]will be,
\[{V_B} = I{R_B} \]
$\Rightarrow {V_B}= 1 \times 6$
$\therefore {V_B}= 6\,V$
Hence, potential difference across \[6\,\Omega \] will be \[6\,V\]

(iv) We know that energy dissipated per second from a circuit element of resistance \[R\] is given by, \[P = {I^2}R\], where \[I\] is the current through the resistance. So, energy dissipated per minute through \[{R_A} = 4\Omega \] will be,
\[E = {I^2}R \times 60 \]
$\Rightarrow E = {1^2} \times 4 \times 60$
$\therefore E = 240\,J$
Hence, energy dissipated per minute through \[4\,\Omega \] resistance will be \[240\,J\] per minute.

Note: The maximum power transfer by a source is possible if the load is equal to the internal resistance of the source. Here, if we consider the \[4\,\Omega \] as the internal resistance of the battery along with \[2\,\Omega \] resistance then power transfer through the \[6\,\Omega \] resistance, taken as load, will be maximum.