Question

A battery of emf 6 V and internal resistance 5 ohms is joined in parallel with another battery of emf 10 V and internal resistance 1 ohm and the combination sends a current through an external resistance of 12 ohm. The ratio of current drawn from 6 V battery to that of 10 V battery is:
A. \[\dfrac{3}{7}\]
B. \[\dfrac{-3}{7}\]
C. \[\dfrac{10}{11}\]
D. \[\dfrac{-10}{11}\]

Answer 1

Hint: In this solution we have been asked to calculate the ratio of current flowing through each battery. Therefore, we will calculate the current flowing through each battery using Kirchhoff’s law. Kirchhoff’s law states that the sum of all the voltages within the loop must be equal to zero. This law is called Kirchhoff's second law.

Complete answer:
It is given that the 6 V battery is in parallel with the 10 V battery both having internal resistance 0.5 ohm and 1 ohm respectively as shown in the figure.
Let the current in batteries be \[{{I}_{1}}\] and \[{{I}_{2}}\] as shown in the figure below.
                                      

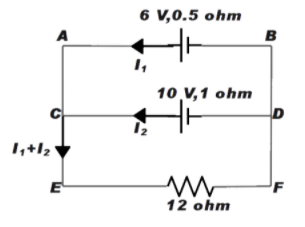
Now, let us apply Kirchhoff’s law at point C
After applying Kirchhoff’s law to loop ABFEA
We get,
\[{{I}_{1}}\times 0.5+({{I}_{1}}+{{I}_{2}})\times 12=6\]
On solving
We get,
\[25{{I}_{1}}+24{{I}_{2}}=12\] …………………. (1)
Similarly, applying Kirchhoff’s law for loop CDFEC
We get,
\[{{I}_{1}}\times 1+({{I}_{1}}+{{I}_{2}})\times 12=10\]
On solving
We get,
\[12{{I}_{1}}+13{{I}_{2}}=10\] ……………………… (2)
After solving (1) and (2)
We get,
\[{{I}_{1}}=-2.27\] and \[{{I}_{2}}=2.86\]
Now taking the ratio,
\[\dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{-2.27}{2.86}\]
We get,
\[\dfrac{{{I}_{1}}}{{{I}_{2}}}=-0.79\]
Now, the closest option to our answer is \[\dfrac{-10}{11}\]

Therefore, the correct answer is option D.

Note:
When applying Kirchhoff’s loop rule, we should identify the closed loop and decide in which direction we go around it. If the wrong direction is selected the magnitude of the potential difference will remain the same however, the direction would be reversed. Kirchhoff’s first law also called as current law states that current flowing into the node is equal to current flowing out of that node.