Answer
428.4k+ views
Hint : The circuit provided in the question is that of a device known as potentiometer. This problem can be solved by understanding the basic principle of potentiometer i.e. the voltage across the resistance is directly proportional to the length at which the galvanometer reads null deflection.
$V \propto l$
$V = kl$
where k = voltage gradient of the potentiometer.
Complete step-by-step answer:
Potentiometer is a device used to calculate the emf and internal resistance of unknown cells by comparing them using a known value. It is loosely based on the principles of metre bridge, which is used to calculate the unknown resistances using the Wheatstone’s network.
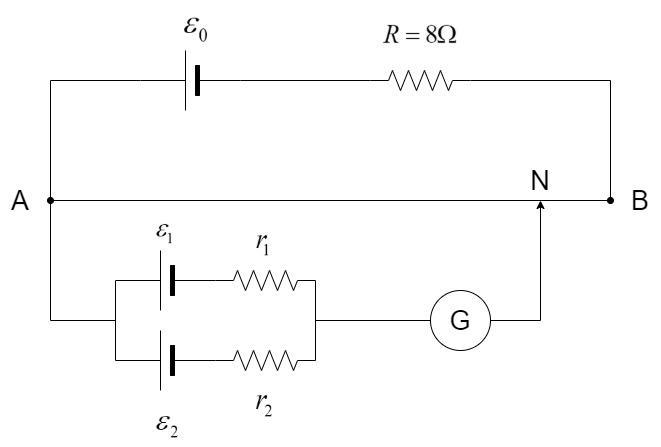
It consists of a uniform wire AB, usually made of constantan. A steady current is maintained at one end of the wire AB and the other end is connected to the cells in study as shown in the circuit diagram below:
The potential gradient of the potentiometer is a constant value. It is taken as standard reference to calculate the emf and internal resistance on the other end of the circuit. The voltage on the other end of the circuit is given by –
$V = KL$
where K = potential gradient and L = length at which null point occurs.
To calculate potential gradient:
The potential gradient is calculated by finding the voltage across the wire AB and dividing it by the length of AB i.e. 4m.
The net resistance of AB, ${R_{AB}}$ = Length of AB $ \times $ Resistance per unit length = $4 \times 4 = 16\Omega $
Given, ${\varepsilon _0} = 12V$
Net resistance in the upper circuit, ${R_{net}} = R + {R_{AB}} = 8 + 16 = 24\Omega $
Current in the upper circuit, $I = \dfrac{{{\varepsilon _0}}}{{{R_{net}}}} = \dfrac{{12}}{{24}} = 0 \cdot 5A$
Hence, voltage drop across AB, ${V_{AB}} = I{R_{AB}} = 0 \cdot 5 \times 16 = 8V$
Given the length of AB, $l = 4m$, the potential gradient of the wire,
$K = \dfrac{{{V_{AB}}}}{l} = \dfrac{8}{4} = 2V{m^{ - 1}}$
To calculate net emf:
The net emf in the other end of the circuit is the combination of the emf and internal resistances of the two cells.
The equivalent emf is given by the formula –
$V = \dfrac{{\dfrac{{{\varepsilon _1}}}{{{r_1}}} - \dfrac{{{\varepsilon _2}}}{{{r_2}}}}}{{\dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}}}}$
Given,
${\varepsilon _1} = 2V$ ${\varepsilon _2} = 4V$ ${r_1} = 2\Omega $ ${r_2} = 6\Omega $
Substituting, we get –
$V = \dfrac{{\dfrac{2}{2} - \dfrac{4}{6}}}{{\dfrac{1}{2} + \dfrac{1}{6}}} = \dfrac{{\dfrac{2}{6}}}{{\dfrac{4}{6}}} = \dfrac{2}{4} = 0 \cdot 5V$
Hence,
The net emf, V = 0.5V Potential gradient, K = 2 V/m
Therefore, length at null deflection is –
$L = \dfrac{V}{K} = \dfrac{{0 \cdot 5}}{2} = 0 \cdot 25m$
Thus, the length at which the galvanometer shows zero deflection is 0.25m.
Note: The reason for using constantan wire is, because the rate of change of resistivity per rise in temperature is very low. Hence, the resistance of the wire remains constant at a wide range of operating temperatures and gives accurate results.
$V \propto l$
$V = kl$
where k = voltage gradient of the potentiometer.
Complete step-by-step answer:
Potentiometer is a device used to calculate the emf and internal resistance of unknown cells by comparing them using a known value. It is loosely based on the principles of metre bridge, which is used to calculate the unknown resistances using the Wheatstone’s network.
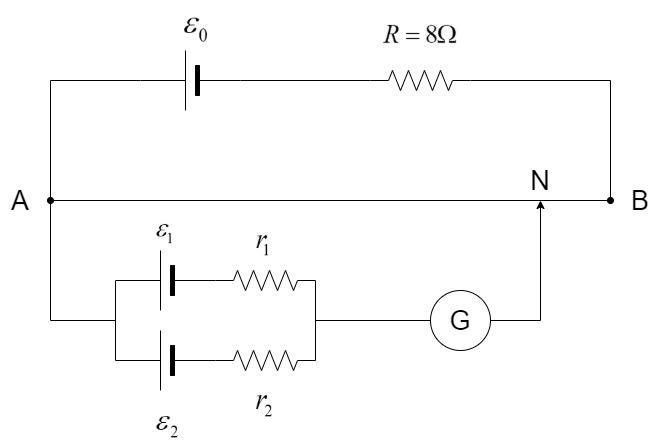
It consists of a uniform wire AB, usually made of constantan. A steady current is maintained at one end of the wire AB and the other end is connected to the cells in study as shown in the circuit diagram below:

The potential gradient of the potentiometer is a constant value. It is taken as standard reference to calculate the emf and internal resistance on the other end of the circuit. The voltage on the other end of the circuit is given by –
$V = KL$
where K = potential gradient and L = length at which null point occurs.
To calculate potential gradient:
The potential gradient is calculated by finding the voltage across the wire AB and dividing it by the length of AB i.e. 4m.
The net resistance of AB, ${R_{AB}}$ = Length of AB $ \times $ Resistance per unit length = $4 \times 4 = 16\Omega $
Given, ${\varepsilon _0} = 12V$
Net resistance in the upper circuit, ${R_{net}} = R + {R_{AB}} = 8 + 16 = 24\Omega $
Current in the upper circuit, $I = \dfrac{{{\varepsilon _0}}}{{{R_{net}}}} = \dfrac{{12}}{{24}} = 0 \cdot 5A$
Hence, voltage drop across AB, ${V_{AB}} = I{R_{AB}} = 0 \cdot 5 \times 16 = 8V$
Given the length of AB, $l = 4m$, the potential gradient of the wire,
$K = \dfrac{{{V_{AB}}}}{l} = \dfrac{8}{4} = 2V{m^{ - 1}}$
To calculate net emf:
The net emf in the other end of the circuit is the combination of the emf and internal resistances of the two cells.
The equivalent emf is given by the formula –
$V = \dfrac{{\dfrac{{{\varepsilon _1}}}{{{r_1}}} - \dfrac{{{\varepsilon _2}}}{{{r_2}}}}}{{\dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}}}}$
Given,
${\varepsilon _1} = 2V$ ${\varepsilon _2} = 4V$ ${r_1} = 2\Omega $ ${r_2} = 6\Omega $
Substituting, we get –
$V = \dfrac{{\dfrac{2}{2} - \dfrac{4}{6}}}{{\dfrac{1}{2} + \dfrac{1}{6}}} = \dfrac{{\dfrac{2}{6}}}{{\dfrac{4}{6}}} = \dfrac{2}{4} = 0 \cdot 5V$
Hence,
The net emf, V = 0.5V Potential gradient, K = 2 V/m
Therefore, length at null deflection is –
$L = \dfrac{V}{K} = \dfrac{{0 \cdot 5}}{2} = 0 \cdot 25m$
Thus, the length at which the galvanometer shows zero deflection is 0.25m.
Note: The reason for using constantan wire is, because the rate of change of resistivity per rise in temperature is very low. Hence, the resistance of the wire remains constant at a wide range of operating temperatures and gives accurate results.
Recently Updated Pages
10 Examples of Evaporation in Daily Life with Explanations

10 Examples of Diffusion in Everyday Life

1 g of dry green algae absorb 47 times 10 3 moles of class 11 chemistry CBSE

What is the meaning of celestial class 10 social science CBSE

What causes groundwater depletion How can it be re class 10 chemistry CBSE

Under which different types can the following changes class 10 physics CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE