Question

A bird is sitting on the top of a vertical pole 20m high and its elevation from a point O on the ground is ${{45}^{\circ }}$ , it flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to ${{30}^{\circ }}$ , then the speed (in m/s) of the bird is
\[\begin{align}
  & A.40\left( \sqrt{2}-1 \right) \\
 & B.40\left( \sqrt{3}-\sqrt{2} \right) \\
 & C.20\sqrt{2} \\
 & D.20\left( \sqrt{3}-1 \right) \\
\end{align}\]

Answer 1

Hint: We will use the following formula to solve this question:
\[\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}},\text{ tan4}{{\text{5}}^{\circ }}=1\text{ and tan3}{{\text{0}}^{\circ }}=\dfrac{1}{\sqrt{3}}\]
Also, the formula of speed is \[\text{Speed=}\dfrac{\text{Distance travelled}}{\text{Time taken}}\] .

Complete step-by-step solution:
To solve this question, first of all, try to get the value of $\tan {{30}^{\circ }}\text{ and tan4}{{\text{5}}^{\circ }}$ by using above stated formula and by making figure to get the points. This will help us to find the base of so formed triangle then, speed can be determined using the above-stated formula.
Let us first understand the problem by drawing a figure. Let A be the point where the bird was sitting first and C be the point where the bird moves in 1 second.

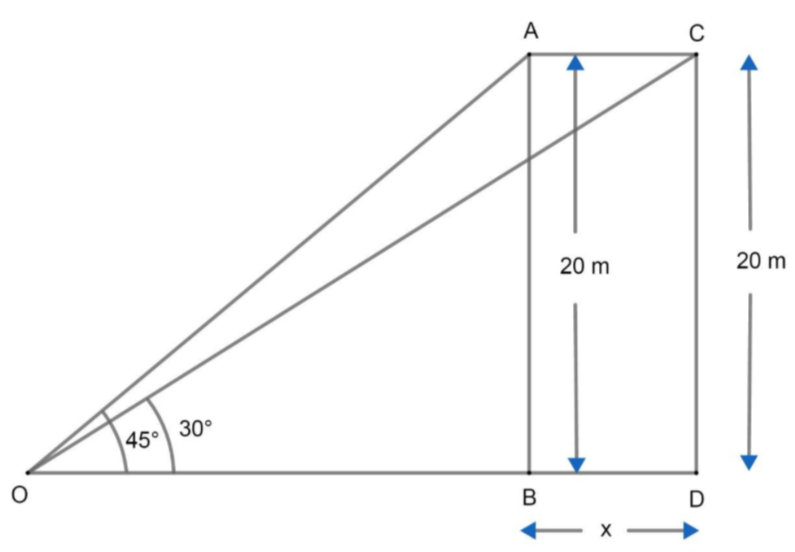
Let ABCD be the vertical pole. Then, height of pole = AB = CD = 20m.
Let O be the point on the ground then, \[\angle AOB={{45}^{\circ }}\text{ and }\angle \text{COB=3}{{\text{0}}^{\circ }}\]
As the pole is vertical to the ground.
So, \[\angle ABO={{90}^{\circ }}\text{ and }\angle \text{CDO=9}{{\text{0}}^{\circ }}\]
Now, consider \[\Delta AOB,\angle AOB={{45}^{\circ }}\]
Applying tan on $\angle AOB$ we have
Formula of $\text{tan}\theta $ in any right angled triangle \[\Rightarrow \text{tan}\theta \text{=}\dfrac{\text{Perpendicular}}{\text{Base}}\]
Here, \[\text{tan}\theta \text{=tan4}{{\text{5}}^{\circ }}\]
\[\begin{align}
  & \text{Perpendicular = AB = 20m and base = OB} \\
 & \Rightarrow \text{tan4}{{\text{5}}^{\circ }}=1=\dfrac{20}{OB} \\
 & \Rightarrow OB=20m\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (i)} \\
\end{align}\]
Again, applying tan on $\angle COD$ we get:
Using above formula of $\text{tan}\theta $ we get:
In \[\Delta COD\] ,
\[\tan {{30}^{\circ }}=\dfrac{CD}{OD}\]
Let side BD = x then OD = OB + x
Now, from equation (i) we have OB = 20m.
\[\Rightarrow OD=20+x\text{ and CD=20}\]
Substituting these values in above equation, we get:
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{20}{20+x}\]
Now, \[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}\]
\[\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{20}{20+x}\]
Cross multiplying above equation, we get:
\[\begin{align}
  & \Rightarrow 20+x=20\sqrt{3} \\
 & \Rightarrow x=20\sqrt{3}-20 \\
 & \Rightarrow x=20\left( \sqrt{3}-1 \right) \\
\end{align}\]
Now, speed of a quantity is \[\text{Speed=}\dfrac{\text{Distance travelled}}{\text{Time taken}}\]
We have assumed distance travelled by bird BD = x and given that time = 1 second.
\[\Rightarrow \text{Speed of bird = }\dfrac{x}{1}=20\left( \sqrt{3}-1 \right)\]
Hence, speed of bird is $20\left( \sqrt{3}-1 \right)$ which is option D.

Note: Students can get confused at the point where the value of x is determined. Remember that, x is the value of distance traveled by bird BD and not the speed of the bird. Always use speed formula as: \[\text{Speed=}\dfrac{\text{Distance travelled}}{\text{Time taken}}\]
Here, time = 1 second. So, the answer did not change but when time differs from 1 second the answer may differ.