Question

A block is kept on a frictionless inclined surface with an angle of inclination $\alpha$. The incline is given an acceleration$\;a$ to keep the block stationary. Then$\;a$ is equal to:
(Take acceleration due to gravity = g)

A. $\dfrac{g}{tan\;\alpha}$
B. $g\;cosec\;\alpha$
C. $\;g$
D. $g\;tan\;\alpha$

Answer 1

Hint: Begin by identifying all the influencing forces that the block is subjected to. This will essentially be gravitational force due to the weight of the block, and a pseudo force due to the acceleration of the incline. Then resolve the forces into their respective horizontal and vertical components and work out which of the components are responsible for gravitational acceleration and linear acceleration. These components will balance each other out, so equate them to arrive at an appropriate expression for the linear acceleration.

Formula used: Gravitational force $F_{g} = mg$
Force due to acceleration $F = ma$

Complete step by step answer:
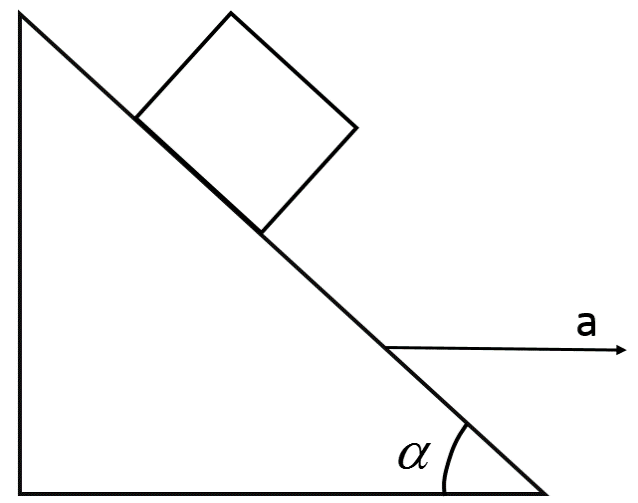
We are given that a block of mass, say$\;m$ is kept on a surface inclined at an angle $\alpha$. In order to prevent the block from moving down the inclined surface, the incline itself is moved with an acceleration$\;a$. The block thus experiences a force due to its weight and a force due to this acceleration.
The force due its weight is the gravitational force acting vertically downwards and is given by:
$F_{g} = mg$, where g is the acceleration due to gravity.
The force experienced by the block due to the acceleration of the incline will be a pseudo force, since it is essentially an inertial force that acts on the whole system as observed in an accelerating frame of reference.
$F_{p} = ma$
This pseudo force is responsible for keeping the block stationary on the inclined surface and acts leftwards from the block as shown in the figure.

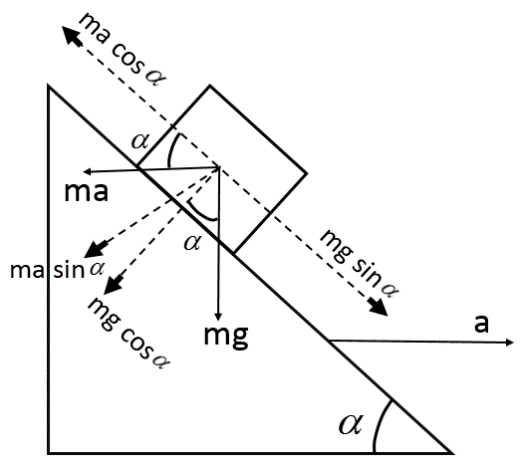
Now, the gravitational force and the pseudo force can be resolved into their respective horizontal and vertical components relative to the incline as shown in the figure.
The block tends to slide down due to the horizontal component of gravity but the horizontal component of the pseudo force acting on the block balances this component of gravity and keeps the block stationary and in position, i.e.,
$ma\;cos\;\alpha = mg\;sin\;\alpha$
$\Rightarrow a = g\;\dfrac{sin\;\alpha}{cos\;\alpha} = g\;tan\;\alpha$

So, the correct answer is “Option D”.

Note: It is very important to remember to separate the components of forces and choose the correctly contributing component for each direction. Also, while resolving the vectors into their horizontal and vertical components, remember to assign the sine and cosine values correctly since it is a common misconception that the horizontal side is always the cosine part and the vertical side is the sine part.