
A block is placed over a large plank (plank is kept on a horizontal surface). The coefficient of friction between the block and the plank is
A. 1 m relative to ground
B. 1 m relative to plank
C. zero relative to plank
D. 2 m relative to ground
Answer
496.5k+ views
Hint: We are given a block kept on a plank and the coefficient of friction between them is given. We need to find the displacement of the block in time 1 s when the plank moves forward horizontally with an acceleration. The displacement of the block will be in opposite to the direction of motion of the plank. We can find this displacement using equations of motion.
Formula used:
Equation of motion
Complete answer:
We have a block placed over a plank.
Let ‘m’ be the mass of the block and ‘M’ be the mass of the plank.
The coefficient of friction,
It is said the block was at rest initially, therefore the initial velocity of the
After a certain time, the plank starts to move forward horizontally, and the acceleration of plank is given
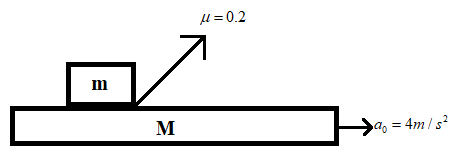
We have to find the displacement of the block, ‘s’ in time 1 s.
Since the plank is moving towards right in a horizontal direction, the block will be displaced in a direction opposite to that of the motion of the plank.
Hence the block will move towards the left horizontally.
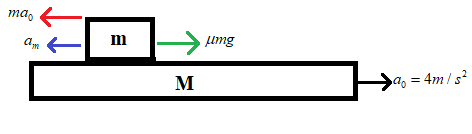
Consider the above figure.
It shows the direction of displacement of the block with respect to plank.
Acceleration of the block is given as
The two forces acting on the block are frictional force,
These two forces are opposite; hence the resultant force will be,
The force acting on the body due to its own motion is
By equating these two forces acting on the body, we get
Substituting the known values in the above equation, we get
Now that we have the acceleration of the block, we have to find the displacement of the block.
According to the third equation of motion, we have displacement as
We know
Therefore,
Therefore displacement of the block in 1 s is 1 m relative to plank.
So, the correct answer is “Option B”.
Note:
The resistance to motion shown by a body with respect to another body is known as friction.
Static friction is the friction experienced by a body at rest when it tries to move another body on its surface.
Coefficient of friction is the ratio of frictional force required to move two sliding surfaces over one another and the total force that is holding them together.
Formula used:
Equation of motion
Complete answer:
We have a block placed over a plank.
Let ‘m’ be the mass of the block and ‘M’ be the mass of the plank.
The coefficient of friction,
It is said the block was at rest initially, therefore the initial velocity of the
After a certain time, the plank starts to move forward horizontally, and the acceleration of plank is given
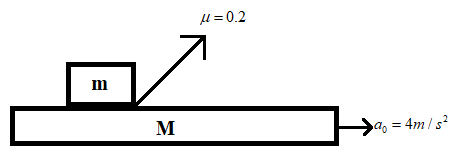
We have to find the displacement of the block, ‘s’ in time 1 s.
Since the plank is moving towards right in a horizontal direction, the block will be displaced in a direction opposite to that of the motion of the plank.
Hence the block will move towards the left horizontally.

Consider the above figure.
It shows the direction of displacement of the block with respect to plank.
Acceleration of the block is given as
The two forces acting on the block are frictional force,
These two forces are opposite; hence the resultant force will be,
The force acting on the body due to its own motion is
By equating these two forces acting on the body, we get
Substituting the known values in the above equation, we get
Now that we have the acceleration of the block, we have to find the displacement of the block.
According to the third equation of motion, we have displacement as
We know
Therefore,
Therefore displacement of the block in 1 s is 1 m relative to plank.
So, the correct answer is “Option B”.
Note:
The resistance to motion shown by a body with respect to another body is known as friction.
Static friction is the friction experienced by a body at rest when it tries to move another body on its surface.
Coefficient of friction is the ratio of frictional force required to move two sliding surfaces over one another and the total force that is holding them together.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




