Question

A block kept on a rough inclined plane, as shown in the figure, remains at rest up to a maximum force 2 N down the inclined plane. The maximum external force up the inclined plane that does not move the block is 10 N. What is the coefficient of static friction between the block and the plane? (Take g = 10 ms$^{ - 2}$)
(A) $\dfrac{2}{3}$
(B) $\dfrac{{\sqrt 3 }}{2}$
(C) $\dfrac{{\sqrt 3 }}{4}$
(D) $\dfrac{1}{4}$

Answer 1

Hint: To find the coefficient of static friction between the block and the plane, we need to make free body diagrams of the body on the plane when the given forces are acting and then solve by applying the concept of equilibrium.

Complete step by step answer:
Our first step for solving such questions is making the free body diagram of the block on the plane. But, two cases are given in the question. One, where a force of 2 N acts on the block in the downward direction along the plane and another, where a force of 10 N acts on the block in the upward direction along the plane. The block is in equilibrium in both the cases. We need to make separate free body diagrams for both the cases. Let us consider the coefficient of static friction to be $\mu $.
For the first case, where a force of 2 N is acting on the block in the downward direction along the plane.

In the free body diagram, we resolve all the force acting on the block in the directions parallel to the plane and perpendicular to the plane. We then equate all the forces in both the directions since the block is in equilibrium.
In the direction perpendicular to the plane, the normal reaction and the cosine component of the weight of the block act in opposite directions and hence balance each other.
${N_1}$ = mg cos(30$^\circ $) = $\dfrac{{\sqrt 3 mg}}{2}$ …equation (1)
In the direction along the plane, the force of friction acts in the upward direction, that is, opposite to the direction of motion. The equilibrium equation along the plane is,
2 + mg sin(30$^\circ $) – ${f_1}$ = 0
The force of friction acting on the block is the product of the coefficient of static friction and the normal reaction acting on the block. Using equation (1), we obtain,
2 + mg sin(30$^\circ $) – $\mu{N_1}$ = 0
$ \Rightarrow 2 + \dfrac{{mg}}{2} - \dfrac{{\sqrt 3 \mu mg}}{2} = 0$ …equation (2)
In the second case, where a force of 10 N acts on the block in the upward direction along the plane.We again resolve the force in the directions parallel and perpendicular to the plane in the free body diagram for this case. We then write the equilibrium equations.The normal reaction and the cosine component of the weight of the block act in opposite directions and hence balance each other.

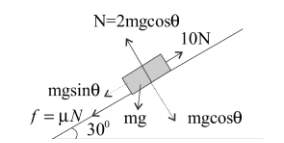
${N_2}$ = mg cos(30$^\circ $) = $\dfrac{{\sqrt 3 mg}}{2}$ …equation (3)
In the direction along the plane, the force of friction acts in the downward direction, that is, opposite to the direction of motion. The equilibrium equation along the plane is,
-10 + mg sin(30$^\circ $) + $\mu{N_1}$ = 0
$\Rightarrow - 10 + \dfrac{{mg}}{2} + \dfrac{{\sqrt 3 \mu mg}}{2} = 0$ …equation (4)
We now add equations (2) and (4) to obtain the value of mg. On adding, we get,
mg = 8
We substitute this value of mg in equation (2) to find the value of the coefficient of static friction.
$therefore\mu = \dfrac{{2 + 4}}{{4\sqrt 3 }} = \dfrac{3}{{2\sqrt 3 }} = \dfrac{{\sqrt 3 }}{2}$

Hence, the correct option is option B.

Note:The force of friction opposes the relative motion between two surfaces. In the second case, where the impending motion is in the upward direction, the friction will act in the downward direction not in the upward direction, whereas in the first case it will act in the upward direction.