Question

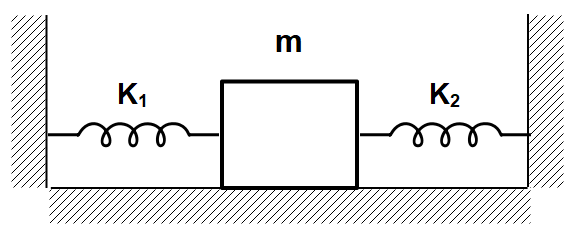
A block of mass m is attached to two unstretched springs of spring constants $K_1$ and $K_2$ as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

A. $\sqrt {\dfrac{{{K_1} + {K_2}}}{m}} x$
B. $\sqrt {\dfrac{{{K_1}{K_2}}}{{m\left( {{K_1} + {K_2}} \right)}}} x$
C. $\sqrt {\dfrac{{{K_1}^2{K_2}^2}}{{m\left( {{K_1}^2 + {K_2}^2} \right)}}} $
D. $\sqrt {\dfrac{{{K_1}^3{K_2}^3}}{{m\left( {{K_1}^3 + {K_2}^3} \right)}}} x$

Answer 1

Hint: Initially, the spring-mass system is undisturbed but when the block is displaced by ‘x’, the work done on the system changes between potential energy and kinetic energy, as per the law of conservation of energy. The system’s energy changes between these two energies. So, we can equate both energies to find the relation between spring constants, mass and velocity.
Formula used:
$(P.E.) = \dfrac{1}{2}K{x^2}$
$(K.E.) = \dfrac{1}{2}m{v^2}$

Complete answer:
In the question, they’ve given a block of mass ‘m’, which is attached to two unstretched springs of spring constants, ‘$K_1$’ and ‘$K_2$’. As the springs are unstretched, there exists no energy in the spring.
Later, the box is displaced to a distance of ‘x’ to the right. So, as we displace the mass the spring 2, gets compressed and the other spring gets extended.

The potential energy of the spring 1 and spring 2 are given by
$\eqalign{
  & {(P.E.)_1} = \dfrac{1}{2}{K_1}{x^2} \cr
  & {(P.E.)_2} = \dfrac{1}{2}{K_2}{x^2} \cr} $
Here,
${K_1}$ and ${K_2}$ are the spring constants of the springs and $x$ is the displacement of the springs.
Similarly, the kinetic energy of the block of mass, ‘m’ is given by
$(K.E.) = \dfrac{1}{2}m{v^2}$
Here,
$m$ is the mass of the block and $v$ is the velocity of the block.
So, as the potential energy itself is changing into kinetic energy, by the law of conservation of energy, we have

$\eqalign{
  & (P.E.) = (K.E.) \cr
  & \Rightarrow \dfrac{1}{2}{K_1}{x^2} + \dfrac{1}{2}{K_2}{x^2} = \dfrac{1}{2}m{v^2} \cr
  & \Rightarrow {v^2} = \dfrac{{{K_1}{x^2} + {K_2}{x^2}}}{m} \cr
  & \Rightarrow v = \sqrt {\dfrac{{{K_1}{x^2} + {K_2}{x^2}}}{m}} = \sqrt {\dfrac{{{K_1} + {K_2}}}{m}} x \cr
  & \therefore v = \sqrt {\dfrac{{{K_1} + {K_2}}}{m}} x \cr} $

So, the correct answer is “Option A”.

Note:
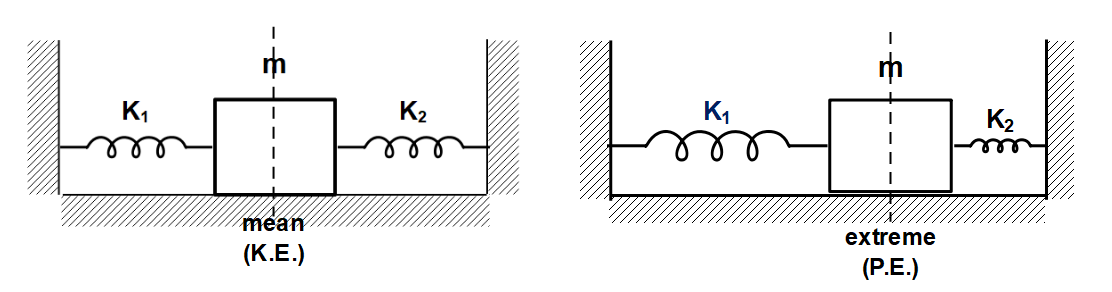
The extension and compression of the springs give rise to potential energy. This potential energy reaches its maximum value when the displacement is maximum, i.e. ‘x’. This potential energy is acquired by the work done in the spring. Once we release the spring, the energy contained as potential energy in the spring changes into kinetic energy of the block, as the block is now free to move. This kinetic energy reaches its maximum value at the mean position, where displacement is zero and the velocity is maximum.