
: A boat moves relative to water with velocity
A.
B.
C.
D.
Answer
495.6k+ views
Hint: In this question, we need to determine the angle at which the boat should move with the stream with the minimum drift to reach the opposite bank of the river. For this, we will use the concept of relative velocity which is the velocity of an object with respect to another object.
Complete step by step answer:
Let the relative velocity of the boat is
The velocity of the river is
Now let the angle be
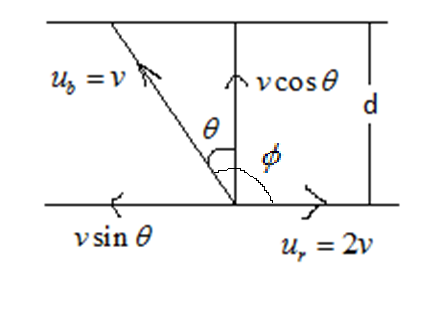
Hence we can write the horizontal and vertical component of velocity of the boat as
Let the width of the river be ‘d’.
So the time required to cross the river will be
Since we have observed that
As we know, drift is
Now for x to be minimum, let’s differentiate equation (iv) w.r.t
By further solving this equation, we get
So the values of the angle
This angle is made with the vertical so, to make the angle with the horizontal axis, add 90 degrees with the 30 degrees to get the result.
Hence, the angle at which the boat shall move with the stream to have minimum drift
Option D is correct.
Note: It is worth noting down here that, the boat can also move with other angles also, but to satisfy the need to the question that there should be minimum drift to reach at directly opposite bank of the river we need to move the boat at an angle of 120 degrees with the horizontal.
Complete step by step answer:
Let the relative velocity of the boat is
The velocity of the river is
Now let the angle be

Hence we can write the horizontal and vertical component of velocity of the boat as
Let the width of the river be ‘d’.
So the time required to cross the river will be
Since we have observed that
As we know, drift is
Now for x to be minimum, let’s differentiate equation (iv) w.r.t
By further solving this equation, we get
So the values of the angle
This angle is made with the vertical so, to make the angle with the horizontal axis, add 90 degrees with the 30 degrees to get the result.
Hence, the angle at which the boat shall move with the stream to have minimum drift
Option D is correct.
Note: It is worth noting down here that, the boat can also move with other angles also, but to satisfy the need to the question that there should be minimum drift to reach at directly opposite bank of the river we need to move the boat at an angle of 120 degrees with the horizontal.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




