
A boat moves with a speed of
A.
B.
C.
D.
Answer
479.7k+ views
Hint:Determine the speed of the boat required to complete one round trip in minimum time which is perpendicular to the river flow. Use the formula for speed of an object to determine the time required for the boat to reach the other edge of the river. Multiply this time by 2 to determine the minimum time for one round trip of the boat.
Formula used:
The speed
Here,
Complete step by step answer:
We have given that the speed of the boat relative to water is
The speed of the water flowing in the river is
The width of the river is
We have asked to determine the minimum time required for one round trip of the boat.The time required for the boat to complete one round trip will be minimum if it is travelled in a direction perpendicular to the flow of water in the river. Let us draw the diagram for the velocities of the boat and water.
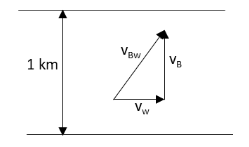
In the above diagram,
Substitute
Hence, the speed of the boat in perpendicular direction is
Now let us determine the time required for the boat to reach the other edge of the river.
Rewrite equation (1) for the speed of the boat.
Substitute
The time
Substitute
Therefore, the time required for the boat for one round trip is
Hence, the correct option is D.
Note: The students should not forget to determine the speed of boat perpendicular to flow of the river because the given speed of the boat relative to water will not give the minimum time required for the boat to complete one round trip in the river. Also, the students should not forget to multiply the determined time by 2.
Formula used:
The speed
Here,
Complete step by step answer:
We have given that the speed of the boat relative to water is
The speed of the water flowing in the river is
The width of the river is
We have asked to determine the minimum time required for one round trip of the boat.The time required for the boat to complete one round trip will be minimum if it is travelled in a direction perpendicular to the flow of water in the river. Let us draw the diagram for the velocities of the boat and water.

In the above diagram,
Substitute
Hence, the speed of the boat in perpendicular direction is
Now let us determine the time required for the boat to reach the other edge of the river.
Rewrite equation (1) for the speed of the boat.
Substitute
The time
Substitute
Therefore, the time required for the boat for one round trip is
Hence, the correct option is D.
Note: The students should not forget to determine the speed of boat perpendicular to flow of the river because the given speed of the boat relative to water will not give the minimum time required for the boat to complete one round trip in the river. Also, the students should not forget to multiply the determined time by 2.
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
EMI starts from ₹3,775 per month
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




