Question

A bob of mass m, suspended by a string of length \[{{l}_{1}}\] is given a minimum velocity required to complete a full circle in the vertical plane. At its highest point, it collides elastically with another bob of mass m suspended by a string of length \[{{l}_{2}}\], which is initially at rest. Both the strings are massless and inextensible. If the second bob after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio is \[\dfrac{{{l}_{1}}}{{{l}_{2}}}\]:

Answer 1

Hint: In this question we have been asked to calculate the ratio of the two strings. Now, we know that during elastic collision of the same masses the final velocity of the bob suspended by string will be the initial velocity for the bob of mass m suspended with string \[{{l}_{1}}\]. We also know the equation for minimum velocity of the string that is required to complete a full circle. Therefore, on equating the two quantities we can calculate the ratio of the strings.
Formula Used:
\[{{v}^{2}}={{u}^{2}}+2as\]
 \[v=\sqrt{5gl}\]

Complete answer:
For a mass suspended with string we know that,
\[T-mgcos\theta =\dfrac{m{{V}^{2}}}{R}\]
At maximum height the tension should be zero for the mass to complete one full circle.
Therefore,
\[\dfrac{mV_{C}^{2}}{R}=-mgcos(180{}^\circ )\]
Therefore,
\[V_{C}^{2}=Rg\]
We can say,
\[{{V}_{C}}=\sqrt{Rg}\] ………….. (1)
Applying the energy conservation for highest and lowest point
We get,
\[\dfrac{1}{2}mV_{A}^{2}=\dfrac{1}{2}mV_{C}^{2}+2mgR\]
Therefore,
\[\dfrac{V_{A}^{2}}{2}=\dfrac{gR}{2}+2gR\]
On solving,
\[V_{A}^{2}=5gR\]
Therefore,
\[VA=\sqrt{5gR}\]
Therefore,
We know that minimum velocity of the string to complete a full circle is given by,
\[v=\sqrt{5gl}\]
  

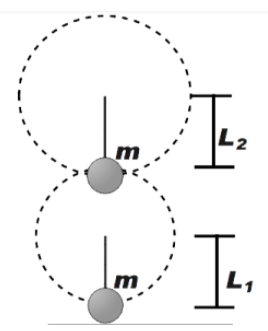
Therefore, the initial velocity \[{{v}_{1}}\] of the bob at A will be given by,
\[{{v}_{1}}=\sqrt{5g{{l}_{1}}}\]
Now the velocity of the bob A when it collides with the bob B can be given by using a second kinematic equation.
\[{{v}^{2}}={{u}^{2}}+2as\]
s is the total distance i.e. \[2{{l}_{1}}\] acceleration will be negative acceleration due to gravity
Therefore,
\[{{v}_{1}}^{2}=5g{{l}_{1}}-2g\times 2{{l}_{1}}\]
Therefore,
\[{{v}_{1}}=\sqrt{g{{l}_{1}}}\]
After collision the bob B will gain initial velocity \[{{u}_{2}}\]. Therefore, conserving the momentum
We get,
\[m{{v}_{1}}=m{{u}_{2}}\]
Therefore,
\[{{v}_{1}}={{u}_{2}}\]
Now the initial velocity of the bob B is \[\sqrt{g{{l}_{1}}}\]. Now this initial velocity should be equal to the minimum velocity required to complete full revolution.
Therefore,
\[\sqrt{g{{l}_{1}}}=\sqrt{5g{{l}_{2}}}\]
Therefore, taking ratio
We get,
\[\dfrac{{{l}_{1}}}{{{l}_{2}}}=5\]
Therefore, the ratio \[\dfrac{{{l}_{1}}}{{{l}_{2}}}=5\]

Note:
Kinematic equations is the set of equations which states the motion of the object moving with constant acceleration. Considering the macro particles the kinematic equations prove to be very helpful. However, At the quantum level these equations render useless as the quantum world is small forces acting on them are different in nature.