Question

A body is moving with a constant speed v in a circle of radius r. Its angular acceleration is:
$\begin{align}
  & a)vr \\
 & b)\dfrac{v}{r} \\
 & c)zero \\
 & d)v{{r}^{2}} \\
\end{align}$

Answer 1

Hint: Obtain the relation between the linear velocity of the particle in circular motion. Further, we can come to a conclusion how the angular speed varies with different quantities. Accordingly we will select the options from the given options.

Complete solution:
To obtain a relation let us assume a particle moving in circular motion from point P to point Q

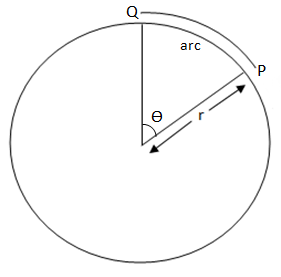
Let us obtain an equation of angular velocity first,
Angular velocity=$\omega =\dfrac{\Delta \theta }{t}$
$\theta $ is the angle between point P and Q,
T is the time taken by the particle to move from P to Q
Since $\Delta \theta =\dfrac{arc}{r}$ , arc =length of PQ,
Dividing the above equation i.e. $\Delta \theta =\dfrac{arc}{r}$ by $\Delta t$,
$\dfrac{\Delta \theta }{\Delta t}=\dfrac{1}{r}\left( \dfrac{arc}{\Delta t} \right)$
R is taken outside the bracket since the radius does change with time.
As t$t\to o$ taking the limits of the above equation,
$\underset{dt\to 0}{\mathop{\lim }}\,\dfrac{\Delta \theta }{\Delta t}=\dfrac{1}{r}\underset{dt\to 0}{\mathop{\lim }}\,\left( \dfrac{arc}{\Delta t} \right)$
$\dfrac{d\Delta \theta }{dt}=\dfrac{1}{r}\dfrac{darc}{dt}$
Since, displacement $\div $ time =$v$ hence
$\dfrac{darc}{dt}=v$ and equation of angular velocity becomes,
$\omega =\dfrac{v}{r}$
$\omega r=v$
Again differentiating the above equation with respect to time,
$\dfrac{dv}{dt}=\dfrac{d\omega r}{dt}$
Using U.V rule to differentiate the product the above equation becomes,
$\dfrac{dv}{dt}=\dfrac{rd\omega }{dt}+\dfrac{\omega dr}{dt}$
$\because \dfrac{dr}{dt}=0$
From kinematics, $\dfrac{dv}{dt}$=linear acceleration of the particle or an object and$\dfrac{d\omega }{dt}$is the angular acceleration of the particle in circular motion. Hence,
$a=r\alpha $
In the above equation, $a$is the linear acceleration $\alpha $is the angular acceleration.
For a particle moving in a circular motion with a constant linear velocity its linear acceleration is zero i.e. $\dfrac{dv}{dt}$=0 , $a$=0 and hence, from the above equation we can conclude that its angular acceleration is also equal to zero from the relation.

Note:
The velocity of the particle or a body keeps on changing as it moves in a circular path. This is because its magnitude of velocity remains the same, but the direction keeps on changing. The direction is given by the tangent to the circle. A circle can be drawn with so many tangents and each tangent has a different direction.