Question

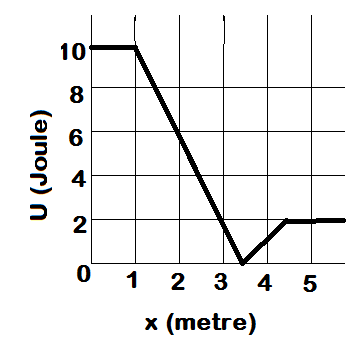
A body with mass 1kg moves in one direction in the presence of a force which is described by the potential energy graph. If the body is released from rest at x = 2m, then its speed when it crosses x = 5m is: (neglect dissipative forces)

A. Zero
B. $1m{s^{ - 1}}$
C. $2m{s^{ - 1}}$
D. $3m{s^{ - 1}}$

Answer 1

Hint:According to the law of conservation of energy in all physical processes taking place in closed systems, the amount of change in kinetic energy is equal to the amount of change in potential energy that is $\Delta U = \Delta K$. If the kinetic energy increases, the potential energy decreases, and vice-versa.
 The other key concept required for this question is the Work-Energy Theorem. According to the work-energy theorem the work done by all forces acting on a particle equals the change in the particle’s kinetic energy.
$\therefore W = \Delta KE = \dfrac{1}{2}(mfv{f^2} - miv{i^2})$


Complete step by step solution:
According to the question:
At x =2m, Potential energy (U) = 6 J
And at x = 5m, Potential energy (U) = 2 J
 Therefore according to conservation of energy we can say that change in kinetic energy is equal to change in Potential energy $\Delta U = \Delta K$.

$\begin{gathered}
  \therefore \Delta U = \Delta KE \\
   \Rightarrow (6 - 2) = \Delta KE \\
   \Rightarrow 4 = \Delta KE \\
   \Rightarrow \Delta KE = 4J \\
\end{gathered} $
Therefore change in kinetic energy = 4 J
And according to work energy theorem we can say that work done by all forces acting on a particle equals the change in the particle’s kinetic energy.
$\begin{gathered}
  \therefore W = \Delta KE = \dfrac{1}{2}(mfv{f^2} - miv{i^2}) \\
  \therefore \Rightarrow 4 = \dfrac{1}{2}(mfv{f^2} - miv{i^2}) \\
\end{gathered} $

$\because $The body is released from rest therefore initial velocity will $(vi)$ be 0.
$\begin{gathered}
  \therefore \Rightarrow 4 = \dfrac{1}{2}(mv{f^2}) \\
   \Rightarrow 8 = mv{f^2} \\
   \Rightarrow 8 = 1 \times v{f^2} \\
   \Rightarrow 8 = v{f^2} \\
   \Rightarrow v{f^2} = 8 \\
   \Rightarrow vf = 2\sqrt 2 \\
    \\
\end{gathered} $
On approximation the final velocity $vf \approx 3m{s^{ - 1}}$

Note: Be clear with the concepts of the work-energy theorem as it helps to reduce many long calculations and sometimes with the use of work-energy theorem we can solve the question without using the integration part as it provides an alternative option to get the answer without using integration.