Question

A border of uniform width is placed around a rectangular photograph that measures 8 inches by 10 inches. If the area of the border is 144 square inches, what is the width of the border, in inches?
A) 3
B) 4
C) 6
D) 8
E) 9

Answer 1

Hint: The area of the rectangle is the product of length and breadth, to find the width we need to add twice the width of the border to the length and breadth.

Complete step by step answer:
Let, the width of the border be x.
Consider the diagram given below.

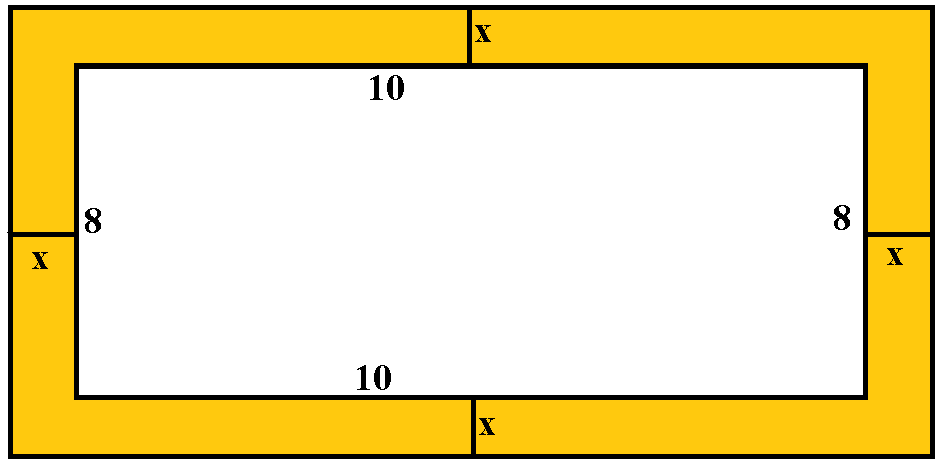
It is given the area of the yellow-colored region is 144 square inches
It is given that the length of the photograph is 10 inches and the breadth of the photograph is 8 inches.
So, the area of the photograph will be equal to the product of length and breadth, i.e., $10 \times 8$ which will be equal to $80\,{\text{square}}\,{\text{inches}}$.
If we need to find the area of the photograph with border, then we have add $2x$ in the length and breadth of the photograph, because the width has to be considered for both sides.
So, the length of the photograph with the border will be $10 + 2x$ and the breadth of the photograph with the border will be $8 + 2x$.
Therefore, the area of photograph with border will be product of length and breadth, i.e., $\left( {10 + 2x} \right)\left( {8 + 2x} \right)$ which will be equal to $\left( {10 + 2x} \right)\left( {8 + 2x} \right) = 80 + 20x + 16x + 4{x^2} = 4{x^2} + 36x + 80$.
Again, it is given in the question that the area of the border is 144 square inches. To find the area of the border we need to subtract the area of the photograph with a photograph with border.
Therefore, ${\text{Area}}\,{\text{of}}\,{\text{photograph}}\,{\text{with}}\,{\text{border}} - {\text{Area}}\,{\text{of}}\,{\text{photograph}} = 144$.
Now, substitute $4{x^2} + 36x + 80$ for ${\text{Area}}\,{\text{of}}\,{\text{photograph}}\,{\text{with}}\,{\text{border}}$and 80 for area of the photograph and find the value of x.
$
  4{x^2} + 36x + 80 - 80 = 144 \\
  4{x^2} + 36x = 144 \\
  4\left( {{x^2} + 9x} \right) = 144 \\
  {x^2} + 9x = 36 \\
  {x^2} + 9x - 36 = 0 \\
 $
Now, factorize the equation ${x^2} + 9x - 36 = 0$ and find the value of x.
$
  {x^2} + 9x - 36 = 0 \\
  {x^2} - 12x + 3x - 36 = 0 \\
  x\left( {x - 12} \right) + 3\left( {x - 12} \right) = 0 \\
  \left( {x - 12} \right)\left( {x + 3} \right) = 0 \\
  x = - 3,12 \\
 $
As the value of x cannot be negative because the width value can never be negative.
Therefore, the width of the border will be 3.


Note:
  In this case, if we assume some value for the width of the border and add them to the length and breadth of the photograph. The difference between the area of the photograph with the border and the area of the photograph will give the area of the border.