Question

A boy standing on a horizontal plane finds a bird flying at a distance of 100m from him at an elevation of $ {30^0} $ . A girl standing on the roof of a 20m high building, finds the angle of elevation of the same bird to be $ {45^0} $ . Both the boy and the girl are on opposite sides of the bird. Find the distance of the bird from the girl.
 $
  (a){\text{ 44}}{\text{.62m}} \\
  (b){\text{ 52}}{\text{.35m}} \\
  (c){\text{ 36}}{\text{.92m}} \\
  (d){\text{ 42}}{\text{.42m}} \\
 $

Answer 1

Hint: In this question let the boy be standing at a point B, the bird flying at point C and the girl standing at point G. Draw a perpendicular from the point C onto the line BD. Use the basic trigonometric ratios ( $ \sin \theta $ ) preferred in respective triangles to get the value of CG.

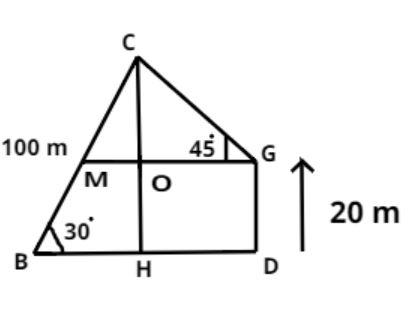
Complete step-by-step answer:

The bird is flying at point C and the position of the boy is at point B.
So according to question
 $ BC = 100 $ meter and $ \angle CBD = {30^0} $ .
Now let us suppose GD be the 20 m high building.
And the girl is standing at point G according to the question and boy and girl are opposite to each other.
Now it is given that the angle of elevation of the bird from the girl is 45 degrees.
 $ \Rightarrow \angle CGM = {45^0} $
Now draw the perpendicular CH online BD.
So in triangle BCH we know that sin is the ratio of perpendicular to hypotenuse.
 $ \Rightarrow \sin {30^0} = \dfrac{{CH}}{{BC}} = \dfrac{{CH}}{{100}} $
Now as we know that sin 30^o = (1/2) therefore
 $ \Rightarrow CH = \dfrac{{100}}{2} = 50 $ meter.

Now by symmetry the length of OH = GD = 20.
Therefore from figure
CH = CO + OH
 $ \Rightarrow 50 = CO + 20 $
 $ \Rightarrow CO = 50 - 20 = 30 $ meter.
Now in triangle COG
 $ \Rightarrow \sin {45^0} = \dfrac{{CO}}{{CG}} = \dfrac{{30}}{{CG}} $
 $ \Rightarrow CG = \dfrac{{30}}{{\sin {{45}^0}}} = \dfrac{{30}}{{\dfrac{1}{{\sqrt 2 }}}} = 30\sqrt 2 = 42.42 $ meter. $ \left[ {\because \sin {{45}^0} = \dfrac{1}{{\sqrt 2 }},\sqrt 2 = 1.414} \right] $
So the distance between the girl and the bird is 42.42 meter.
Hence option (D) is correct.

Note: In these types of questions it is always advisable to draw the diagrammatic representation using the information provided in the question as it helps understanding the geometry of the figure involved. Basic understanding of symmetric length like OH = GD in this case, helps getting to answer.