
A boy was asked to find the LCM of 3, 5, 12 and another number. But while calculating, he wrote 21 instead of 12 and yet came with the correct answer. What could be the fourth number?
Answer
564k+ views
Hint: LCM refers to the least common multiple among the given numbers. It is given that in both cases, the LCM calculated was the same. Then the fourth number will be the product of those numbers that aren’t common between the two cases because only then the LCM will be the same.
Complete step-by-step answer:
Let the fourth number be x.
Then the numbers in respective cases are:
Case 1: 3, 5, 12, x
In the next case he wrote 21 instead of 12, so
Case 2: 3, 5, 21, x
The number different in the cases are 12 and 21, their prime factorization is given as:
\[
\Rightarrow {12 = 2 \times 2 \times 3} \\
\Rightarrow {21 = 7 \times 3}
\]
For the LCM to be the same in both the cases, the fourth number should be the product of those numbers which are uncommon between the factors of 12 and 21, therefore:
\[
\Rightarrow x = 7 \times 2 \times 2 \\
\Rightarrow x = 7 \times 4 \\
\]
x = 28
Thus the fourth number is 28.
This can also be verified by equating the LCMs in both cases by substituting the value of x.
LCM (3, 5, 12, 28) = LCM (3, 5, 21, 28)
The prime factors for both LHS and RHS can be written as:
\[3 \times 5 \times 3 \times 2 \times 2 \times 7 \times 2 \times 2 = 3 \times 5 \times 7 \times 2 \times 2 \times 7 \times 2 \times 2\]
Taking common values out of these for LCM:
\[3 \times 2 \times 2 \times 7 = 3 \times 2 \times 2 \times 7\]
420 = 420
It is proved the LCM is the same for both the cases.
Therefore, the fourth number the boy took for calculating LCM is 4.
Note: To avoid confusion calculate LCM after writing prime factors like:
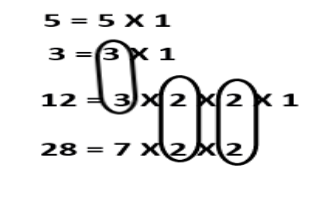
The LCM here will be \[3 \times 2 \times 2 \times 5 \times 7\]
Remember: the pair among the factors will be counted only once whereas the numbers occurring not in pairs will be written as it is.
LCM calculated cannot be less than either of the numbers.
Prime factors are those numbers whose factors are one and number itself.
Complete step-by-step answer:
Let the fourth number be x.
Then the numbers in respective cases are:
Case 1: 3, 5, 12, x
In the next case he wrote 21 instead of 12, so
Case 2: 3, 5, 21, x
The number different in the cases are 12 and 21, their prime factorization is given as:
\[
\Rightarrow {12 = 2 \times 2 \times 3} \\
\Rightarrow {21 = 7 \times 3}
\]
For the LCM to be the same in both the cases, the fourth number should be the product of those numbers which are uncommon between the factors of 12 and 21, therefore:
\[
\Rightarrow x = 7 \times 2 \times 2 \\
\Rightarrow x = 7 \times 4 \\
\]
x = 28
Thus the fourth number is 28.
This can also be verified by equating the LCMs in both cases by substituting the value of x.
LCM (3, 5, 12, 28) = LCM (3, 5, 21, 28)
The prime factors for both LHS and RHS can be written as:
\[3 \times 5 \times 3 \times 2 \times 2 \times 7 \times 2 \times 2 = 3 \times 5 \times 7 \times 2 \times 2 \times 7 \times 2 \times 2\]
Taking common values out of these for LCM:
\[3 \times 2 \times 2 \times 7 = 3 \times 2 \times 2 \times 7\]
420 = 420
It is proved the LCM is the same for both the cases.
Therefore, the fourth number the boy took for calculating LCM is 4.
Note: To avoid confusion calculate LCM after writing prime factors like:
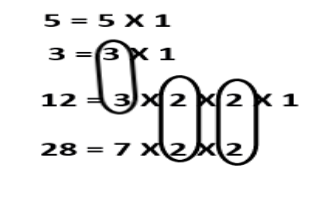
The LCM here will be \[3 \times 2 \times 2 \times 5 \times 7\]
Remember: the pair among the factors will be counted only once whereas the numbers occurring not in pairs will be written as it is.
LCM calculated cannot be less than either of the numbers.
Prime factors are those numbers whose factors are one and number itself.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Which one of the following groups comprises states class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

A couple went for a picnic They have 5 sons and each class 8 maths CBSE

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE




