
A bridge across a river makes an angle of
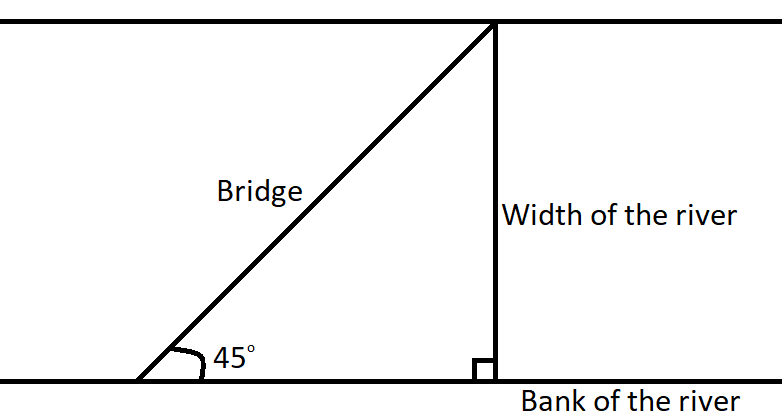

Answer
505.5k+ views
1 likes
Hint: In this question we have to find the width of the river when we are given the length of the bridge and the angle made by the bridge with the bank of the river. It is given in the figure that there is formation of a right angle triangle in which the bridge is acting as the hypotenuse and the width o f the river is the perpendicular of the right angle triangle. As it is right angle triangle we can apply the trigonometric function like taking the sine of the given angle we can find the width of the river when length of the bridge is given, the relation becomes
Complete step-by-step answer:
In this question we are given that there is formation of a right angle triangle such that it's hypotenuse is the bridge laid over the river and the perpendicular of the triangle is the width of the river. We are also given that the angle made by the bridge with one of the bank of the river is
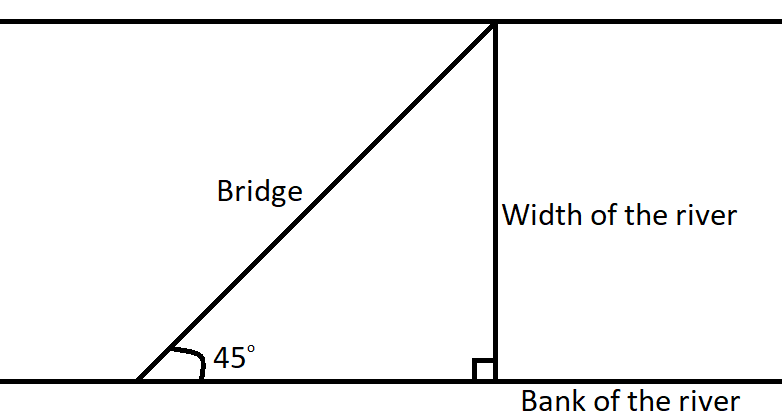
Now in the question we have to find the width of the river by using the information given above but first we need a relation to connect the width of the river with the length of the bridge and the angle made by the bridge with the banks of the river included in the triangle.
It is given that the triangle is right angle triangle so which means that we can apply the trigonometric functions on the triangle to find the missing elements of the triangle by using the values of known elements. In this case we need to find the width of the river which acts as the perpendicular to the triangle by using the length of bridge which acts as hypotenuse of the same, so we will use the sine function of the given angle which is as follows,
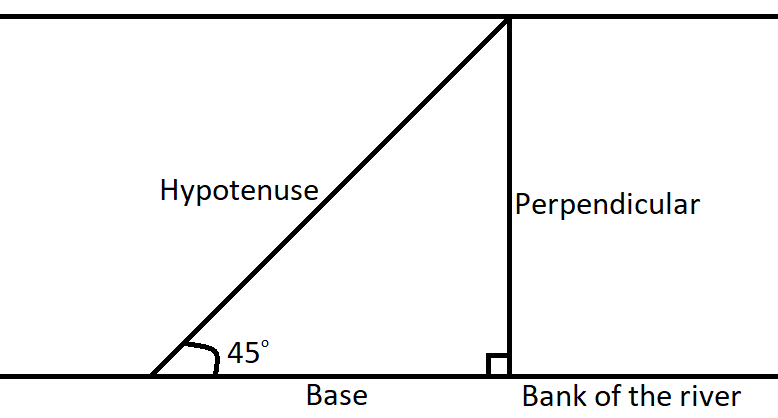
Let us assume the length of the perpendicular be
Putting the known values in the function, we get,
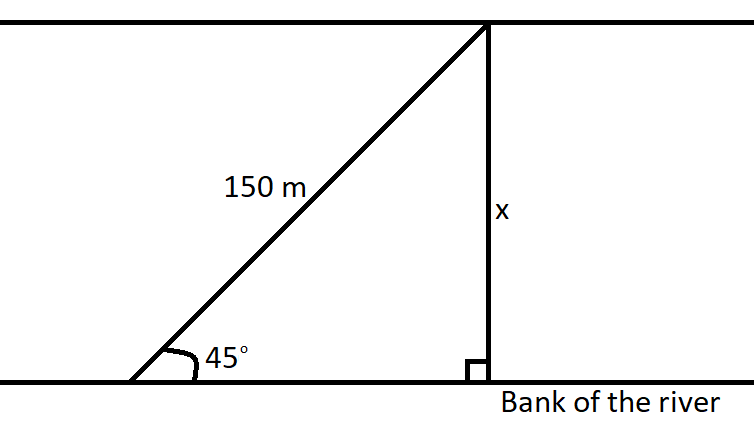
We need to remember the values of trigonometric functions on some particular angles in this case the value of
Now solving the sine function when applied to the triangle, we get,
Now the width of the river comes out to be
Note: One should remember the values of all 6 trigonometric functions at some particular angles. We can also do the question by using cosecant function
Complete step-by-step answer:
In this question we are given that there is formation of a right angle triangle such that it's hypotenuse is the bridge laid over the river and the perpendicular of the triangle is the width of the river. We are also given that the angle made by the bridge with one of the bank of the river is

Now in the question we have to find the width of the river by using the information given above but first we need a relation to connect the width of the river with the length of the bridge and the angle made by the bridge with the banks of the river included in the triangle.
It is given that the triangle is right angle triangle so which means that we can apply the trigonometric functions on the triangle to find the missing elements of the triangle by using the values of known elements. In this case we need to find the width of the river which acts as the perpendicular to the triangle by using the length of bridge which acts as hypotenuse of the same, so we will use the sine function of the given angle which is as follows,

Let us assume the length of the perpendicular be
Putting the known values in the function, we get,

We need to remember the values of trigonometric functions on some particular angles in this case the value of
Now solving the sine function when applied to the triangle, we get,
Now the width of the river comes out to be
Note: One should remember the values of all 6 trigonometric functions at some particular angles. We can also do the question by using cosecant function
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




